10 es fizika feladatok megoldással
Három fogyasztót sorba kapcsoltunk, melyeknek ellenállásai: R1=15 Ω , R2= 35 Ω , R3 = 30 Ω. Számold ki az erdő ellenállást!
Ohm törvénye ✔️ teljes összefoglaló ✔️ 10 példán keresztül!
Cikkünkben egy A – Z komplett összefoglalót szerettünk volna olvasóink elé tárni Ohm törvényével kapcsolatban, mely gyakorlatilag mindent magában foglal, melyet egy érettségizőnek vagy dolgozatírónak tudnia kell. A gyakorlati példák mellett fontos, hogy az elmélettel is tisztában legyünk.
Az egyszerű áramkör felépítése
Egy áramkörben töltéshordozók haladnak egy zárt hurokban, vagy zárt körben. Az áramkör az alábbi részekre bontható:
- Feszültséggenerátor
- Ellenállás (fogyasztó)
- Vezető
A töltéshordozók áramlása hozza létre az áramot. Az áram jele I, mértékegysége Amper [A].
Ahhoz, hogy az áram létrejöhessen, valamilyen energiaforrásra van szükség. Ezt egy elektromos erő szolgáltatja, melyet feszültségnek hívunk. A feszültség jele U, mértékegysége Volt [V].
Amennyiben a feszültséggenerátor által gerjesztett feszültség mértékét ismerjük, akkor egyetlen egyéb tényező van, ami figyelembe kell vennünk az áramerősség számításakor, és ez pedig az ellenállás mértéke (eredő ellenállás). Az ellenállás annak a mértéke, hogy az adott áramkörben található elem milyen mértékben akadályozza a töltéshordozók áramlását. Az ellenállás jele R, mértékegysége Ohm [V].
Felmerül bennünk a teljesen jogos kérdés: a vezetőnek mégis milyen szerepe van abban, hogy mekkora lesz az áramerősség? A vezető ellenállása is befolyásolja az áramkörben megjelenő áram erősségét, az iskolai példákban ezt általában elhanyagoljuk, vagy pedig az áramkörben jelzett ellenállás értéke jelzi ezt az értéket.
Ha a hétköznapi életben szeretnénk egy példát látni, akkor nincs más dolgunk, mint hogy egy zseblámpaizzót különböző feszültségű elemekhez kapcsoljunk. Amennyiben az elem feszültsége nagyobb, a zseblámpa erősebb fénnyel világít.
Ohm törvénye
Ohm törvénye kimondja, hogy a vezetőn keresztül folyó áram mértéke egyenesen arányos a feszültséggel, és fordítottan arányos a vezető ellenállásával. Az arányossági tényező maga az ellenállás, melyet hasonlíthatnánk a közegellenálláshoz is. Minél nagyobb az ellenállás, annál kisebb lesz a létrejövő áramerősség, és minél kisebb az ellenállás, annál nagyobb lesz a keletkező áram, hiszen a töltéshordozók mozgása kevésbé akadályozott. Másképp megfogalmazva: egy fogyasztó két kivezetése közt mérhető feszültség és a fogyasztón áthaladó áram erőssége között egyenes arányosság van.
Mindez talán kissé elvonatkoztatottnak tűnhet elsőre. Akkor hasonlítsuk az egyszerű áramkört egy csőrendszerhez. Amennyiben a csőben nagyobb a nyomás, vagy nagyobb a cső keresztmetszete, több víz fog azon átfolyni egységnyi idő alatt. Ugyanígy szemléltethetünk egy áramkört is: a cső keresztmetszete szemlélteti az ellenállást, a víz nyomása szemléleti a feszültséget, míg a létrejövő áramot szemlélteti a cső keresztmetszetén egységnyi idő alatt átfolyó víz mennyisége.
Mindezek után – az ismert jelöléseket használva – öntsük képlet formájába Ohm törvényét:

Amennyiben szeretnénk, megteremthetjük a megfelelő mértékegységek közti összefüggést is:
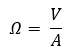
A képletek átrendezésével megkaphatjuk a másik két mennyiséggel kifejezve az áramerősséget és a feszültséget is:

Nagyon sokszor szokták a diákok összekeverni a képletben szereplő elemeket. Ehhez szeretnénk az alábbi kis szemléltető ábrát bemutatni, melyet háromszög-módszerként is ismerünk. A háromszög belsejét osszuk három részre az alábbi módon a felső részbe mindképp az U kerüljön, az alsó két részbe pedig az I és R tetszőleges sorrendben. A háromszög felső részében található mennyiség kifejezhető az alatta levő két mennyiség szorzatával. A háromszög alsó szintjein levő elemek pedig úgy, hogy a felső elemet osztjuk az alul található másik elemmel, tehát, például R = U / I mindezek alapján.

Grafikus ábrázolás
Ábrázoljuk egy adott áramkörben keletkező áramerősséget a feszültség függvényében, ha az ellenállás mértékék változtatjuk. Az alábbi grafikont fogjuk kapni, rendre R1, R2, R3, stb… ellenállások függvényében:
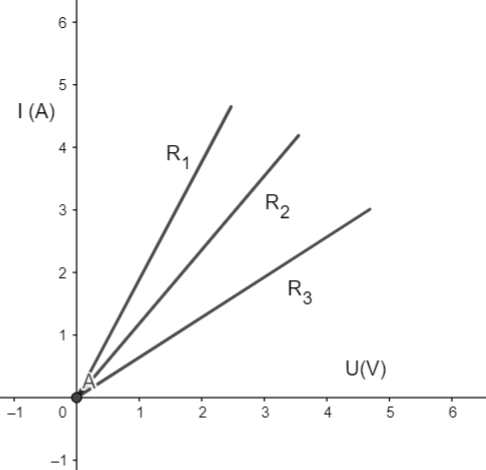
Minél nagyobb volt az ellenállás mértéke, annál kevésbé volt az egyenes meredek. Minden esetben egyenest kaptunk, ha az ábrázolást adott ellenállás mellett elvégeztük. Ennek az az oka, hogy a feszültség és áramerősség között egyenes arányosság áll fent, az arányossági tényező pedig maga az ellenállás.
Hogyan számíthatjuk ki párhuzamos és soros ellenállások eredőjét?
Az áramkörben természetesen jelenhetnek meg soros és párhuzamos ellenállások is. Mégis hogyan kell az áramkörben keletkező áramerősséget kiszámolni, ha több ellenállás is megfigyelhető az áramkörben?
Sorba kapcsolt ellenállások eredője az egyes ellenállások mértékének az összege.

Ez esetben az egyes ellenállásokon eső feszültségek összege a tápfeszültséggel egyezik meg.
Párhuzamos kapcsolás esetén az erdő ellenállás reciproka egyenlő az egyes ellenállások reciprokösszegével.
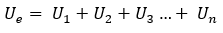
Párhuzamos kapcsolás esetén minden egyes ellenálláson azonos feszültség esik.

Hogyan számíthatjuk ki egy fémes vezeték ellenállását?
A mérések igazolták, hogy egy fémes vezeték ellenállása függ annak
- keresztmetszetétől
- hosszától
- annak fajlagos ellenállásától
A fajlagos ellenállás (ϱ) egy, az anyagra jellemző arányossági tényező. A vezető ellenállása egyenesen arányos a vezető hosszával és fajlagos ellenállásával, és fordítottan arányos a vezető keresztmetszetével.
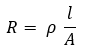
A fajlagos ellenállás SI mértékegysége:

A fajlagos ellenállásból nagyon könnyen származtatható a fajlagos vezetőképesség, hiszen a fajlagos vezetőképesség a fajlagos ellenállás reciproka.
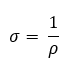
Hogyan számítható egy vezeték ellenállása a hőmérséklet függvényében?
A vezető fajlagos ellenállása természetesen függ a hőmérséklettől is. A hőmérséklet növekedésével a fajlagos ellenállás mértéke is nő, az alábbi összefüggés érvényes:
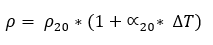

A való életben hol jelenik meg Ohm törvénye?
A saját háztartásodban biztos, hogy rengeteg olyan készülék és kütyü található, amely rendelkezik LED izzóval. Az autóelektronikában is számtalan olyan alkatrész figyelhető meg, ahol a LED világítás megjelenik.
A mérnökökre pedig hatalmas felelősség hárul, amikor ezeket a LED áramköröket megtervezik. Amennyiben túl kicsi a LED fogyasztón eső áram, akkor az nem fog világítani, vagy pedig nagyon halványan. Abban az esetben, ha túl erős az áramerősség, akkor az izzó akár tönkre is mehet. Tehát, pontosan be kell lőnünk az áramerősség mértékét A LED igényeinek megfelelően. Az áramerősség mértékét az úgynevezett előtét ellenállással lehet szabályozni, de vigyázzunk a számításkor! Hiszen a LED-nek és a vezetéknek, valamint a generátornak is van ellenállása a valóságban, ezeket is figyelembe kell vennünk.
Hogyan mérhetjük meg egy ellenállás mértékét?
A fizika érettségin, valamint a témazáró dolgozatban is nagyon gyakran jön elő az úgynevezett Wheatstone-mérőhíd. Ez arra használható, hogy az egy ellenállás nagyságát meghatározzuk.
Gyakorló feladatok
Mindig a gyakorlat teszi a mestert. Ha szeretnéd megérteni Ohm törvényét, akkor íme, lássunk néhány gyakorló feladatot!
I. feladat
Egy tűzhely ellenállása 16 Ω. A rákapcsolt áramforrás feszültsége 9V. Mekkora az átfolyó áram erőssége?
Megoldás.
Használjuk az alábbi, jól ismert képletet!
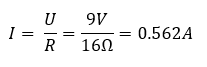
II. feladat
Az R = 80 Ω ellenállású fogyasztót U = 230V feszültségre kapcsoljuk. Mekkora a rajta áthaladó áram?
Megoldás.
Használjuk az alábbi, jól ismert képletet!
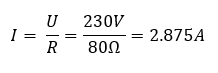
III. feladat
A mérési eredmények szerint a vezetőn áthaladó áramerősség mérték 3A, miközben a vezető végei közt mérhető feszültség 10V. Mekkora a vezető elektromos ellenállása?
Megoldás.
Használjuk Ohm törvényét! A képlet szerint
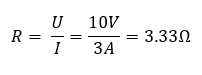
IV. feladat
Mekkora töltésmennyiség halad át a vezető keresztmetszetén 1 óra alatt, ha az áramerősség I = 5mA?
Megoldás.
Használjuk ki azt a tényt, hogy a vezetőn áthaladó töltésmennyiség mindig egyenesen arányos az idővel, valamint az áram nagyságával. Mindebből következik – az egyenes arányosságot feltételezve – hogy Q = 18C mennyiségű töltés halad át a vezetőn ezen idő alatt.
V. feladat
A mérési eredmények szerint az egyszerű áramkörben a fogyasztón eső feszültség 20V, míg a vezeték ellenállása . Mekkora a fogyasztón átfolyó áramerősség mértéke?
Megoldás.
Használjuk az alábbi képletet!

Egy kis érdekesség
Ahogy ezt már sokszor megszokhattuk a fizikában – de ez általában ugyanígy igaz a különféle tudományágakra is – sokszor találkozni furcsa, ismeretlen nevekkel, mikor egy tételt, vagy egy méretékegységet nevezünk el.
Amikor az egyszerű áramkör fogalmával ismerkedünk, akkor három új nevet hallottunk. A Volt [V] a feszültség mértékegysége, az Amper [A] az áramerősségé, míg Ohm [Ω] az ellenállásé. Természetesen mindhárom fogalom mértékegységét valódi személyekről nevezték el.
André-Marie Ampére a XIX. század első felében az árammál átjárt vezetők tulajdonságait vizsgálta, valamint ezek mágnenes kölcsönhatásait.
Alessandro Volta dolgozta ki annak idején az elektromos áram elméletét, egy időben tevékenykedett Ampéreval.
Georg Simon Ohm volt az a személy, aki megalkotta Ohm törvényét: azt a törvényszerűséget, amely egyértelmű összefüggést teremt az egyszerű áramkörben megtalálható feszültség, áramerősség és eredő ellenállás között.
Természetesen mindhármuk munkássága az elektrosztatika témaköréhez kapcsolódik.
Összefoglalás
Habár talán elsőre nem így gondolnánk, Ohm törvénye a középiskolai, valamint általános iskolás tananyagnak egyik azon része. melyet sok évvel később sem szabad elfelejtenünk, még akkor sem, ha már felálltunk az iskolapadból. Hiszen az elektromos berendezések – tervezésüket tekintve – melyeket használunk a hétköznapjainkban, mind-mind Ohm törvényét veszik figyelembe, mikor az áramerősség nagyságát határozzák meg. Ma már szinte el sem lehetne képzelni az életünket azon törvényszerűség nélkül, melyet egy zseniális német mérnök alkotott meg másfél évszázaddal ez előtt.
10 es fizika feladatok megoldással
A közöltek csak megoldásvázlatok , esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.
P. 3416. A Föld mely részén és hogyan tölthető el két vasárnap egy szombat és a rákövetkező hétfő között? (3 pont)
Takács Gábor, Budapest
Megoldás. A vasárnap-hétfő vonal közvetlen közelében. Amikor ezen a vonalon éjfél van, az egész Földön ugyanolyan nap van, de tőle keletre éppen kezdődik (0 óra), míg nyugatra éppen befejeződik (24 óra). Ha tehát a vasárnap-hétfő vonalnál szombatról vasárnapra virradólag a vonaltól nyugatra tartózkodunk, de a következő éjfélkor a befejeződő vasárnapból átlépünk a vonal keleti oldalán kezdődő vasárnapba, egymás után két vasárnapot is eltölthetünk.
P. 3417. Nagyméretű digitális órát készítettünk, ami az órát és a percet mutatja. A percek jelzéséhez 14 db fénycsövet használtunk fel, amelyek mindegyike átlagosan 2160 üzemóra után kiég. Az órát 2001. január elsején 00 óra 00 perckor indítottuk. A percet jelző fénycsövek közül várhatóan melyik és mikor ég ki elsőként, illetve várhatóan melyik és mikor ég ki utolsóként? (3 pont)
Közli: Sári Péter, Budapest
Megoldás. A 10 perceket jelző helyen a 0,1,2. 5 számjegyek óránként 10 percet, a percek helyén a 0,1,2. 9 számjegyek pedig óránként összesen 6 percet vilagítanak. Ebből megállapítható, hogy a legtöbbet (óranként 9×6 percet) a perceket jelző helyen a jobb alsó függőleges cső működik, míg a legkevesebbet (óranként 2×10 percet) a 10 perceket jelző helyen a bal alsó függőleges cső világít. Az első esetben 2400 óra alatt telik ki a várható élettartam, ez 100 nap, ami április 10-én éjfélkor jár le.
Hasonlóan, a legkevesebbet működő cső várható élettartama 270 nap alatt telik el, azaz szeptember 27-én éjfélkor (pontosabban 30 perccel hamarabb, mert a kérdéses cső utoljára a 23. óra 30. percében világít, amikoris 23:29-et mutat az óra -, de nem érdemes ilyen pontosan számolni, mert a várható élettartam csak egy átlagos érték).
Megjegyzés: A fénycsöveket és hasonló eszközöket nagymértékben öregítik a ki-be kapcsolások. Ezt a tényt a figyelembe véve is a korábbi megfontolással kapott fénycső ég ki a leghamarabb (legkésőbb), hisz azt kapcsolják ki-be a legtöbbször (legkevesebbszer).
P. 3418. Két egyenlő sugarú, 30 \(\displaystyle Omega\) ellenállású, rézből készült körvezetőt úgy forrasztunk ösze, hogy egymás középpontjain átmennek. A forrasztási pontokra 12 V-os akkumulátort kapcsolunk.
a ) Mekkora az egyik kisebb íven átfolyó áram erőssége?
b ) Mekkora az akkumulátor által leadott teljesítmény? (3 pont)
Közli: Farkas László (Newton-Kupa feladat), Keszthely
Megoldás. a ) 1,2 A; b ) 43,2 W.
P. 3419. Egy vadász a feje felett 100 méter magasban eltalál egy húzó vadlibát, amely a vadásztól 60 méterre esik a földre. Körülbelül hány méterrel és hány fokkal kellett a madár elé céloznia, ha a lövedék sebessége 400 m/s volt? (4 pont)
Közli: Szabó Gergő, Heves, Eötvös J. Gimn.
Megoldás. A leesés ideje \(\displaystyle t=\sqrt=4,5\) s. Az s =60 m vízszintes útból a liba sebessége v = s / t =13,4 m/s. A lövedek \(\displaystyle tau\)=0,25 s alatt ér fel h =100 m magasra, ennyi idő alatt a liba \(\displaystyle Delta\) s = v\(\displaystyle tau\) =3,35 m-t tett meg, tehát ennyivel kellett eléje célozni. Ez 0,0335 radiannak, azaz 1,9 o -nak felel meg.
Megjegyzés: A számítás során a lövedék mozgását egyenletesnek tekintettük, nem vettük figyelembe a sebességének (1 százaléknál is kisebb) változását. Ebben a közelítésben a puska ,,előre tartási szöge” független a magasságtól, csak a vadliba és a lövedék sebességének arányától függ. Csillagászatban az ehhez hasonló jelenséget (a távcső ,,célzási irányának” a Föld mozgása miatt szükséges módosítását) aberrációnak nevezik.
P. 3420. Egy hosszú, egyenes vonalzó fekszik a vízszintes asztalon. A vonalzót az egyik végéhez kötött fonal segítségével vízszintesen húzzuk. Ha a fonal a vonalzó hossztengelyével párhuzamos, akkor F 0 erő szükséges a test megmozdításához. Mekkora erővel lehet a vonalzót megmozdítani, ha a fonal merőleges a hossztengelyre? (A vonalzó egyenletesen nyomja az asztalt.) (4 pont)
Közli: Brájer László, Budapest
Megoldás. A megcsúszáskor a rúdra merőleges F erő hatására a rúd egy, a húzott végétől x távolságra eső pontja körül (éppen 0 szöggyorsulással) elfordul. Az erők és a forgatónyomatékok egyensúlyából
\(\displaystyle x=l/\sqrt\,,\quad\quad F=F_0(\sqrt-1)\approx041F_0,\)
(ahol kihasználtuk, hogy mg\(\displaystyle mu\) = F 0 ).
P. 3421. Alaszkai aranyásók népes csoportja egy széles folyóhoz érkezik. A túlsó parton – éppen szemben – egy hatalmas aranyrögöt pillantanak meg. Amelyikük először odaér, az kapja meg a bányaművelés jogát. Milyen útvonalat válasszon Joe, ha ugyanolyan gyorsan tud evezni a vizen, mint gyalogolni a szárazföldön. Számítsuk ki és rajzoljuk le Joe legkedvezőbb útvonalát, ha sebességének és a folyó sebességének aránya az aranymetszés arányszámánál a ) nagyobb, b ) kisebb. (Az optimális útvonal meghatározásánál grafikus módszert is használhatunk.) (5 pont)
Szokoly Gyula feladata nyomán
Megoldás. Legyen a folyó szélessége D , a víz sebessége v , és jelölje w azt a sebességet, amivel Joe futni, illetve evezni tud. Tegyük fel, hogy Joe először átevez a folyón, majd a partot érés helyétől felszalad az aranyröghöz. Ha csónakja vízhez viszonyított sebessége a vízével \(\displaystyle pi\)/2+\(\displaystyle alpha\) szöget zár be, a folyóra merőlegesen w cos\(\displaystyle alpha\) sebességgel halad, miközben v – w sin\(\displaystyle alpha\) sebességgel csurog lefelé. Ennek megfelelően t 1 = D /( w cos\(\displaystyle alpha\)) idő alatt ér át, és s =( v – w sin\(\displaystyle alpha\)) t 1 távolsággal az aranyrög alatt ér partot. Ezt az utat t 2 = s / w = D ( v – w sin)/( w 2 cos) idő alatt teszi meg. Így az aranyrög elérése az \(\displaystyle alpha\) szög függvényében
időt vesz igénybe. Ha \(\displaystyle alpha\)-t egy kicsi \(\displaystyle Delta\) értékkel megváltoztatjuk t (\(\displaystyle alpha\))
értékre változik. Ennek levezetésekor kihasználtuk, hogy kis \(\displaystyle alpha\) esetén sin\(\displaystyle Delta\), cos1, [így sin(+)sin+cos, cos(+)cos-sin], és azt, hogy , a () 2 nagyságú tagokat pedig elhanyagoltuk. (Ezek a közelítések annál jobbak, minél kisebb a .) Ha t () minimális, értéke semmilyen mellett sem csökkenhet, ilyenkor tehát a együtthatója nulla, azaz
ami éppen az aranymetszés nevezetes arányszáma.
A fenti eredmény a differenciálszámítás formális szabályainak alkalmazásával, vagy az
függvény ( R = v / w ) grafikus vizsgálatával is megkapható.
P. 3422. Kilenc ponttöltést helyezünk el egy 1 cm rácsállandójú, 3×3-as négyzetrács rácspontjaiban. A töltések nagyságát úgy választjuk meg, hogy az egyes töltések helyén a többi töltésből származó potenciál 10 kV legyen. Mekkora a töltések összes kölcsönhatási energiája? (5 pont)
Közli: Bakonyi Gábor, Budapest
Megoldás. Egy töltésrendszerben a kölcsönhatási energia
Jelen esetben minden töltés helyén a többi azonos U potenciált hoz létre, azaz i -től függetlenül
A szimmetriából nyilvánvaló, hogy csak háromféle töltés van a rendszerben. Jelölje Q 1 a csúcsokon, Q 2 az élek közepén, Q 3 pedig a középpontban található töltést. Ezekre az U egyenletéből Q 1 =0,052 Ua / k , Q 2 =0,213 Ua / k es Q 3 =0,442 Ua / k adódik, ahol a a rácsállandó.
A rendszer össztöltése: 4 Q 1 +4 Q 2 + Q 3 =1,50 Ua / k =1,67 . 10 -8 C, így E =7,5 . 10 -5 J.
P. 3423. Az ábrán látható szabályos háromszög alakú vezető keret egyik, mozgatható oldalát egyenletesen, v =0,1 m/s sebességgel csúsztatjuk végig a másik két oldalon. A vízszintes keret függőleges irányú, homogén, B =0,4 T indukciójú mágneses mezőben van. Az oldalak hosszúsága l =1 m, ellenállásuk 1 .
a ) Hogyan változik időben a körben indukált elektromotoros erő?
b ) Hogyan változik időben az áramerősség?
c ) Mennyi munkát végzünk a csúsztatáskor, ha a súrlódás elhanyagolható? (5 pont)
Közli: Gálfi László, Budapest
Megoldás. A vezető keret területe az idő függvényében
Ennek megfelelően az indukált elektromotoros erő
Mivel az ellenállás
tehát időben nem változik. A csúsztatáshoz szükséges pillanatnyi teljesítmény P = UI , azaz
ami a teljes T időre felösszegezve
P. 3424. Egy adiabatikusan zárt rendszer két testet tartalmaz. Az A test hőkapacitása 4000 J/K és hőmérséklete 2400 K, a B test hőkapacitása 8000 J/K és hőmérséklete 300 K. Mekkora munka nyerhető ki ebből a rendszerből (mint hőerőgépből)? (6 pont)
Schwartz Lajos emlékverseny, Nagyvárad
Megoldás. Kapcsoljunk – gondolatban – a két test (mint két hőtartály) közé egy ideális hőerőgépet, és azzal végeztessünk munkát. E gépet olyan kicsi teljesítményűnek gondoljuk, hogy egy ciklusa alatt a hőtartályok hőmérséklete állandónak tekinthessük.
Egy ciklus alatt az A test által leadott, illetve B által felvett hőre igaz, hogy
Tekentellel arra, hogy jelen esetben C B =2 C A , fennáll
2 T A T B + T B T A =0,
ami a ( T A T B 2 ) =0 egyenlettel egyenértékű. Ez utóbbi megoldása ( T A T B 2 ) =állandó (és ez az állandó a testek ismert kezdeti hőmérsékletéből számítható). Ennek megfelelően a teljes folyamat végére kialakuló közös hőmérséklet
A rendszerből kivett (maximálisan kivehető) munka az A test által leadott és a B test által felvett hőmennyiség különbsége:
Adatainkkal K és L =4,8 MJ.
P. 3425. Milyen egy kerékpár küllős kerekének képe a célfotón? (A célfotó úgy készül, hogy a célvonal nagyon keskeny sávjáról nagyon sűrűn egymás után elektronikus kamerával felvételeket készítenek, majd ezeket egymás mellett, a kerékpár várható haladási sebességének megfelelő távolságban helyezik el.) (6 pont)
Közli: Bodor András, Budapest

Megoldás. A felvétel folyamatát úgy is elképzelhetjük, ahogy azt a kerek tengelyehez rögzitett, de nem forgó koordinata-rendszerből látnánk: az álló tengelyű, de szögsebességgel forgó kerékről egy R sebességgel haladó keskeny, függőleges résen keresztül készítünk felvételeket egy álló fotólemezre. Tekintsük t =0-nak azt a pillanatot, amikor a tengely áthalad a célvonalon. A egész mozgás erre a pillanatra való időtükrözésre szimmetrikus, ezért a kép is szimmetrikus lesz, így elég az egyik felét nézni. A kerék abroncsa nyilván körneknek látszik, a küllők képe a kérdéses. Vegyük origónak a kerek tengelyét, mutasson az x tengely balra, az y pedig lefelé, és tekintsük azt a küllőt, amelyik a t =0-ban szöget zár be a függőlegessel. A t pillanatban a küllő szöge , és az a pontja látszik a képen, amelyikre x = Rt . Ekkor az . A küllő képe r és polárkoordinátákkal kifejezve:
Ez az egyenlet különböző, de rögzített értékeket választva sorra megadja az egyes küllők képét (lásd a vázlatos ábrát).
Comments are closed, but trackbacks and pingbacks are open.