Matematika középszintű érettségi feladatok 2003-2020

The guards at the Tower of London (0) are called Yeoman Warders. In principle they are responsible (1) looking after any prisoners at the Tower and safeguarding the British crown jewels, but in practice they act as tour guides and are (2) tourist attraction in their own right. Nobody knows more about the history of the Tower (3) them and no visit is complete without joining one of their tours. Having guarded this royal palace and fortress for centuries they will fascinate you with amazing stories, passed on (4) generation to generation.

2005 május – Közép Matek Érettségi

You should change to the original language for a better experience. If you want to change, click the language label or click here!

Ebben a kurzusban megoldjuk a 2005 májusi középszintű matematika érettségi összes feladatát. A feladatok megoldási menetét nagyon részletesen elmagyarázzuk, hogy ha legközelebb is találkoztok hasonló feladatokkal, akkor ne okozzon problémát számotokra azok megoldása. Reméljük, hogy ez a kurzus.

Ebben a kurzusban megoldjuk a 2005 májusi középszintű matematika érettségi összes feladatát. A feladatok megoldási menetét nagyon részletesen elmagyarázzuk, hogy ha legközelebb is találkoztok hasonló feladatokkal, akkor ne okozzon problémát számotokra azok megoldása. Reméljük, hogy ez a kurzus hasznos lesz az érettségi előtt álló és fiatalabb diákok számára is!
A feladatok forrása az oktatas.hu. A videókat néhány éve érettségizett diákok készítették. A videókban elhangzottakért semmilyen felelősséget nem vállalunk.

1

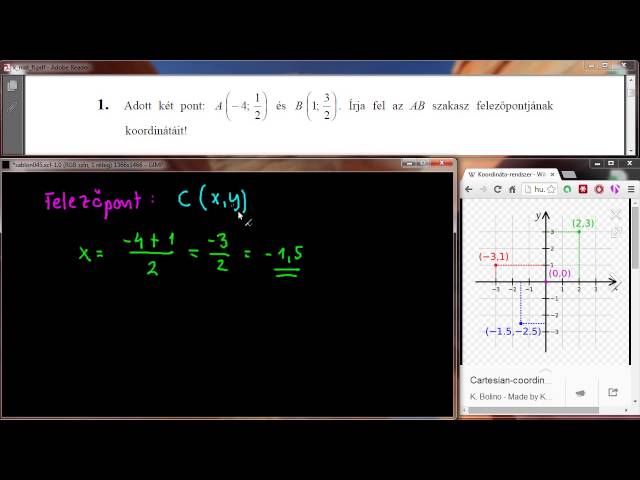
Adott két pont: A(-4;1/2) és B(1;3/2). Írja fel az AB szakasz felezőpontjának koordinátáit! (Forrás: http://www.oktatas.hu)

2

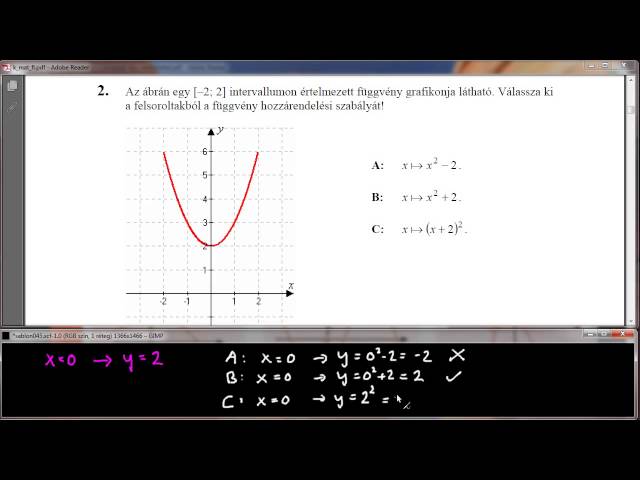
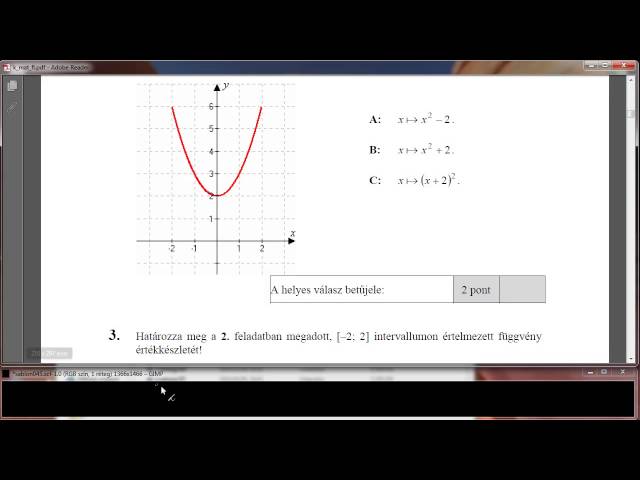
Az ábrán egy [-2; 2] intervallumon értelmezett függvény grafikonja látható. Válassza ki a felsoroltakból a függvény hozzárendelési szabályát! (Forrás: http://www.oktatas.hu)

3

Határozza meg a 2. feladatban megadott, [-2; 2] intervallumon értelmezett függvény értékkészletét! (Forrás: http://www.oktatas.hu)

4

Döntse el, hogy a következő állítások közül melyik igaz és melyik hamis!
A: A háromszög köré írható kör középpontja mindig valamelyik súlyvonalra esik.
B: Egy négyszögnek lehet 180°-nál nagyobb belső szöge is.
C: Minden trapéz paralelogramma. (Forrás: http://www.oktatas.hu)

5

Egy kör sugarának hossza 4, középpontja a (–3; 5) pont. Írja fel a kör egyenletét! (Forrás: http://www.oktatas.hu)

6

Egy rendezvényen 150 tombolajegyet adtak el. Ági 21-et vásárolt. Mekkora annak a valószínűsége, hogy Ági nyer, ha egy nyereményt sorsolnak ki? (A jegyek nyerési esélye egyenlő.) (Forrás: http://www.oktatas.hu)

7

Egy derékszögű háromszög egyik befogójának hossza 3 cm, a vele szemközti szög 18,5°. Mekkora a másik befogó? Készítsen vázlatot, és válaszát számítással indokolja! (Forrás: http://www.oktatas.hu)

8

Egy mértani sorozat első tagja 8, hányadosa 1/2. Számítsa ki a sorozat ötödik tagját! (Forrás: http://www.oktatas.hu)

9

Egy gráfban 4 csúcs van. Az egyes csúcsokból 3; 2; 2; 1 él indul. Hány éle van a gráfnak? (Forrás: http://www.oktatas.hu)

10

11

A szóbeli érettségi vizsgán az osztály 22 tanulója közül az első csoportba öten kerülnek.
a) Hányféleképpen lehet a 22 tanulóból véletlenszerűen kiválasztani az első csoportba tartozókat? (Forrás: http://www.oktatas.hu)

12

A szóbeli érettségi vizsgán az osztály 22 tanulója közül az első csoportba öten kerülnek. Először mindenki történelemből felel.
b) Hányféle sorrendben felelhet történelemből az 5 kiválasztott diák? (Forrás: http://www.oktatas.hu)

13

Egy gömb alakú labda belső sugara 13 cm. Hány liter levegő van benne? Válaszát indokolja! (Forrás: http://www.oktatas.hu)

14

Oldja meg a következő egyenletet a valós számok halmazán!
cos^2 x + 4*cos x = 3*sin^2 x .(Forrás: http://www.oktatas.hu)

15

Egy számtani sorozat második tagja 17, harmadik tagja 21.
a) Mekkora az első 150 tag összege? (Forrás: http://www.oktatas.hu)

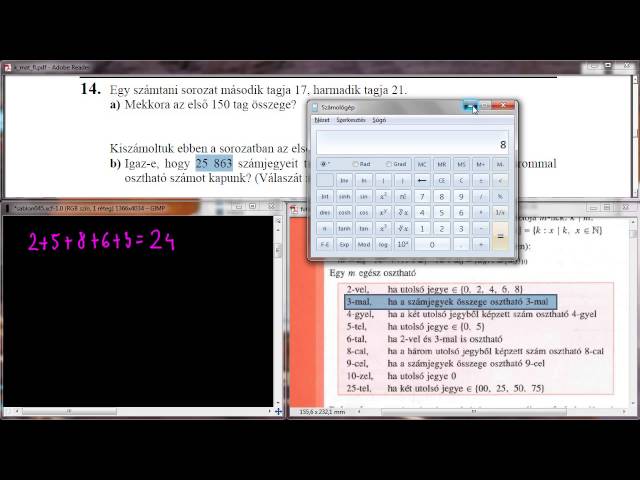
16

Egy számtani sorozat második tagja 17, harmadik tagja 21. Kiszámoltuk ebben a sorozatban az első 111 tag összegét: 25863.
b) Igaz-e, hogy 25863 számjegyeit tetszőleges sorrendben felírva mindig hárommal osztható számot kapunk? (Válaszát indokolja!)
(Forrás: http://www.oktatas.hu)

17

Gábor olyan sorrendben írja fel 25 863 számjegyeit, hogy a kapott szám néggyel osztható legyen. Milyen számjegy állhat a tízes helyiértéken? (Válaszát indokolja!)
(Forrás: http://www.oktatas.hu)

18

Egy dolgozatnál az elérhető legmagasabb pontszám 100 volt. 15 tanuló eredményeit tartalmazza a következő táblázat:
Elért pontszám:100 95 91 80 65 31 17 8 5
A dolgozatok száma: 3 2 1 2 1 2 2 1 1
a) Határozza meg az összes dolgozat pontszámának átlagát számtani közepét), móduszát és.

19

A dolgozatok érdemjegyeit az alábbi táblázat alapján kell megállapítani!
Pontszám Osztályzat
80 — 100 jeles
60 — 79 jó
40 — 59 közepes
20 — 39 elégsége.

20

c) Készítsen kördiagramot az osztályzatok megoszlásáról! Adja meg az egyes körcikkekhez tartozó középponti szögek értékét is! (Forrás: http://www.oktatas.hu)

21

Anna és Zsuzsi is szeretné megvenni az újságosnál az egyik magazint, de egyik lánynak sincs elegendő pénze. Anna pénzéből hiányzik a magazin árának 12%-a, Zsuzsi pénzéből pedig az ár egyötöde. Ezért elhatározzák, hogy közösen veszik meg a magazint. A vásárlás után összesen 714 Ft-juk.

22

Anna és Zsuzsi is szeretné megvenni az újságosnál az egyik magazint, de egyik lánynak sincs elegendő pénze. Anna pénzéből hiányzik a magazin árának 12%-a, Zsuzsi pénzéből pedig az ár egyötöde. Ezért elhatározzák, hogy közösen veszik meg a magazint. A vásárlás után összesen 714 Ft-juk.

23

Egy rejtvényújságban egymás mellett két, szinte azonos rajz található, amelyek között 23 apró eltérés van. Ezek megtalálása a feladat. Először Ádám és Tamás nézték meg figyelmesen az ábrákat: Ádám 11, Tamás 15 eltérést talált, de csak 7 olyan volt, amelyet mindketten észrevettek.
a).

In order to view our videos and try our tests, log in or register quickly completely free. After registration you get access to numerous extra features as well!

24

Egy rejtvényújságban egymás mellett két, szinte azonos rajz található, amelyek között 23 apró eltérés van. Ezek megtalálása a feladat. Először Ádám és Tamás nézték meg figyelmesen az ábrákat: Ádám 11, Tamás 15 eltérést talált, de csak 7 olyan volt, amelyet mindketten észrevettek.

25

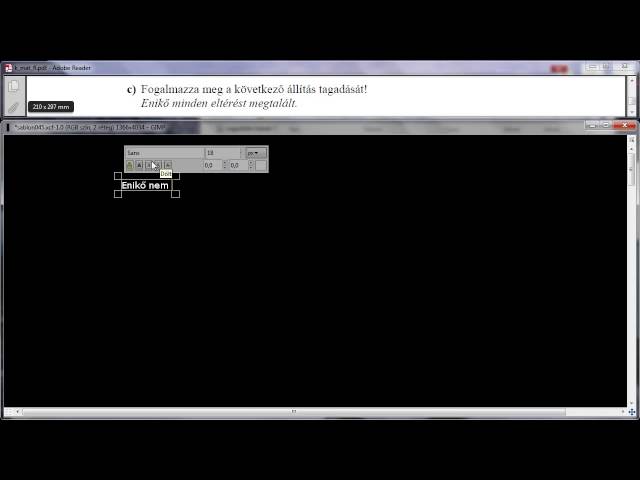
c) Fogalmazza meg a következő állítás tagadását!
“Enikő minden eltérést megtalált.”
(Forrás: http://www.oktatas.hu)

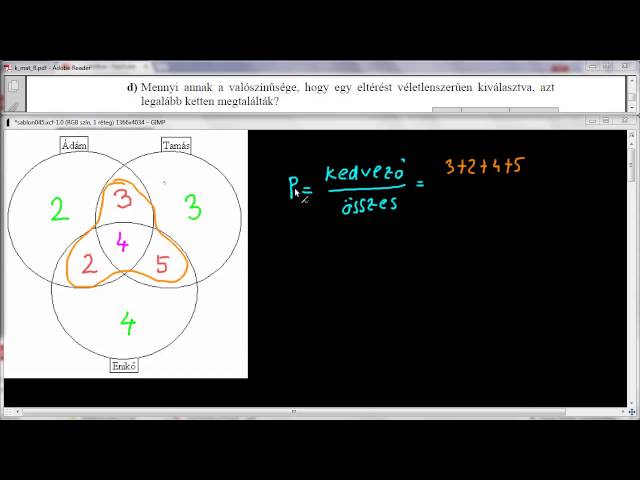
26

Matematika középszintű érettségi feladatok 2003-2020 május.pdf

6 мая 2020 г. . Négy különböző gyümölcsfából egyet-egyet ültetek sorban egymás . Bontsa fel a 36 000-et két részre úgy, hogy a részek aránya 5:4 legyen!

Matematika középszintű érettségi feladatok 2003-2020 május.pdf – kapcsolódó dokumentumok

6 мая 2020 г. . Négy különböző gyümölcsfából egyet-egyet ültetek sorban egymás . Bontsa fel a 36 000-et két részre úgy, hogy a részek aránya 5:4 legyen!

25 июн. 2014 г. . érettségi feladatsorok feladatait típusaik alapján rendszerezze. . az A halmaz elemei közül azokat a számokat, amelyek megoldásai a √ 2.

27 июн. 2017 г. . b) A 20-nál kisebb pozitív prímszámok összege páratlan! c) A deltoid átlói felezik a belső szögeket! 21. (2008. május, 8. feladat, 2 pont).

Háromszögek egybevágóságának alapesetei. Sokszögek egybevágóságának fogalma. 12) Hasonlósági transzformációk fogalma, tulajdonságai.

A központi matematika érettségi bevezetése 1959-ben kezdő- dött. Ekkor az érettségi írásbeli és szóbeli részből állt. A felvételizők számára 1973-ban.

005 elején érettségi előtt álló diákokkal írattam kétféle matematika próbaérettségit: egy hagyományos, (továbbiakban régi típusú) és egy középszintű, .

Az érettségi vizsga írásbeli vizsgarészén a vizsgabizottság munkáját . történelem, magyar nyelv és irodalom), a felügyelő tanár ellenőrzi azt is, .

21 апр. 2020 г. . A felügyelő tanár középszintű érettségi vizsga esetén a vizsgát szervező intézmény igazgatójától kapja . Egészségügyi technikai ismeretek.

27 июн. 2017 г. . Korábban elkészítettem a közép szintű matematika érettségi feladatok . (2006. február, 2. feladat, 12 pont: 2 + 6 + 4).

Két elektroszkóp; ebonit-vagy műanyag rúd; ezek dörzsölésére szőrme vagy műszálas textil; üvegrúd; ennek dörzsölésére bőr vagy száraz újságpapír.

3. tétel: A nem nyelvi jelek kommunikációs eszközei. II. témakör: A magyar nyelv története. 4. tétel: Nyelvemléktípusok. 5. tétel: Nyelvtörténeti korszakok.

26 мая 2020 г. . piros, zöld, kék, sárga, rózsaszín, fehér, barna / . zöld – kék zöld – sárga zöld – rózsaszín zöld – fehér zöld – barna 5 lehetőség .

18 мая 2020 г. . Magyar irodalom – haladó Részletek Molnár F.: A Pál utcai fiúk c. regényből . Munkafüzet 78. o./4. 5. feladat. 2. Munkafüzet 79. o.

5 мая 2020 г. . Második felesége neve: Ezen a szigeten élte életének utolsó éveit: Szorgalmi (internet segítségével):. 1. Ki volt Napóleon második .

Információs társadalom (3 tétel) . Informatikai alapismeretek – hardver (6 tétel) . Az operációs rendszer fogalma, feladata, fajtái.

Fizika középszintű érettségi mérések és kísérletek. 2020. Összeállította: Szemánné Majoros Anikó szaktanár. Page 2. 2. A mérések és kísérletek felsorolása.

9. tétel: Egynyelvű szótárak. A NYELVI SZINTEK. 10. tétel: A morfémák, szóelemek szerepe és helyes használata a szóalak felépítésében, a szószerkezetek .

Az apostol szerepe Petőfi életművében. 2. Arany János nagykőrösi korszakának balladái. 3. A világháború motívuma Ady Endre költészetében.

14 мая 2020 г. . vizsgajelentkezéseket az Oktatási Hivatal törli. Ha a tanuló a 12. évfolyam végén valamely tantárgyból elégtelen értékelést kap, abból a.

A bárium-klorid moláris tömege: M(BaCl2) = 208,3 Č. . A dinitrogén-tetroxid hány százaléka bomlott el nitrogén-dioxiddá, ha a gázelegy sűrűsége.

28 янв. 2015 г. . Topográfiai feladatok. Magyarország földrajzából középszintű érettségire. A feladatok megoldásához atlasz nem használható.

15 окт. 2013 г. . Számítsa ki a sorozat első tagját! . tanár számára nem derül ki egyértelműen, hogy melyik feladat értékelését . c) A „Ki nevet a végén?

13 окт. 2015 г. . Az alábbi függvények a pozitív számok halmazán értelmezettek: . Az öttusa úszás számában 200 métert kell úszni.

8 мая 2018 г. . Terjedelem: 8 darab A4-es oldal. Az egyes példányok címzettjei: az 1. számú példányt kapja. OH irattár. Másolati példányok készítése: A .

8 мая 2018 г. . Egy fagylaltozóban hatféle ízű fagylalt kapható: vanília, csokoládé, puncs, eper, málna és dio. Andrea olyan háromgombócos fagylaltot .

8 мая 2012 г. . maximális pontszám elért pontszám. I. rész. 1. feladat. 2. 2. feladat. 2. 3. feladat. 2. 4. feladat. 3. 5. feladat. 2. 6. feladat.

6 мая 2014 г. . Egy osztályban 25-en tanulnak angolul, 17-en tanulnak németül. E két nyelv közül leg- alább az egyiket mindenki tanulja.

3 мая 2016 г. . Időtartam: 45 perc. Pótlapok száma. Tisztázati. Piszkozati. EMBERI ERŐFORRÁSOK. MINISZTÉRIUMA. ÉRETTSÉGI VIZSGA ○. 2016. május 3.

5 мая 2009 г. . Ervin és Frédi két magányos jegenyefa távolságát szeretnék meghatározni, de . Először kerestek egy olyan tereppontot, ahonnan a két fa .

5 мая 2009 г. . átlók száma szimmetriatengelyek száma az egy csúcsból húzható különböző hosszúságú átlók száma a legrövidebb átló hossza .

2007. október 25. 8:00. I. Időtartam: 45 perc . A rajzterem falát (lásd az ábrán) egy naptár díszíti, melyen három forgatható korong található.

született meg a sárospataki országgyűlés határozata, és értékelje annak politikai, katonai jelentőségét! A Rákóczi-szabadságharc. „9. végzés.

A feladat Mária Terézia vámrendeletéhez kapcsolódik. (K/rövid). Mutassa be a források és ismeretei felhasználásával a rendelet kiadásának gazdasági okait!

Mutassa be az ábra, a szöveg és ismeretei segítségével a görög hitvilág . és ismeretei segítségével az ókori keleti vallások és a zsidó vallás között.

Érettségi esszék – Egyetemes jelenkor, középszint . történelem nagy jelentőségű neveinek a tömegéből ki kell választani a legnagyobbakat, és olyan módon.

5 мая 2020 г. . A feladatok mellett található szürke téglalapok közül az elsőben a feladatra adható ma- ximális pontszám van, a javító által adott pontszám .

17 окт. 2017 г. . A két háromszög szögei páronként egyenlők, így a két háromszög valóban hasonló. . (Az ABC és a CAD háromszögek hasonlósága miatt).

16 окт. 2012 г. . Időtartam: 45 perc. Pótlapok száma. Tisztázati. Piszkozati. EMBERI ERŐFORRÁSOK. MINISZTÉRIUMA. ÉRETTSÉGI VIZSGA ○. 2012. október 16.

8 мая 2018 г. . Megjegyzés: Ha a vizsgázó a csonkakúp teljes felszínével vagy csak a palást területével szá- mol, akkor legfeljebb 7 pontot kaphat.

18 окт. 2011 г. . Időtartam: 45 perc. Pótlapok száma. Tisztázati. Piszkozati. NEMZETI ERŐFORRÁS. MINISZTÉRIUM. ÉRETTSÉGI VIZSGA ○. 2011. október 18.

2014 május matek érettségi megoldás

A cikk már legalább egy éve nem frissült, az akkor még aktuális információk lehet, hogy mára elavultak.

Nincs mit tenni, a matematika kötelező érettségi tantárgy! A diákok számára csak annyi választási lehetőség van, hogy eldönthetik: közép vagy emelt szinten szeretnének érettségizni. A két szint között a legfontosabb különbségek: középszinten csak írásbeli megmérettetés van, emelt szinten szóbeli vizsga is van; más a feladatok mennyisége és a feladatok nehézsége.

Ahhoz, hogy el tudd dönteni, melyik szintet válaszd, röviden ismertetjük az érettségire vonatkozó szabályokat!

A szint megválasztásához ad segítséget azon felsőoktatási szakok listája, ahol megkövetelik a matematika emelt szintű érettségi vizsgát. Az emelt szintű érettségiért összesen 100, azaz vizsgatárgyanként 50 többletpont jár – ehhez minimum 45 százalékos eredményt kell elérni. Ha a kiválasztott szakon az adott tárgy kötelező vagy választható, csak akkor jár a többletpont.

• Erdőmérnöki- matematika/biológia/kémia/fizika/szakmai előkészítő tárgy emelt szinten
• Andragógia, pedagógia, pszichológia szakokra jelentkezők is tehetnek matematikából emelt szintű vizsgát.
• Alkalmazott gazdaságtan – matematikából kötelező emelt szintű vizsgát tenni
• Gazdaságelemzés – matematikából kötelező emelt szintű vizsgát tenni
• Építész- matematika vagy fizika vagy építészeti és építési alapismeretek emelt szinten
• Energetikai mérnöki- matematika vagy fizika emelt szinten
• Építészmérnöki- matematika vagy fizika vagy építészeti és építési ismeretek emelt szinten

Sok szakra előírnak egy emelt szintű érettségi vizsgát, ez lehet a matematika is.

Az egyik legfontosabb változás ez évben az, hogy matematikából nem lehet előrehozott érettségi vizsgát tenni.

A középszintű érettségi

Írásbeli

Időtartam: 180 perc (45 + 135)
Elérhető pont: 100 pont
Használható segédeszközök : függvénytáblázat (akár többféle is lehet egyidejűleg, szöveges adatok tárolására és megjelenítésére nem alkalmas zsebszámológép, vonalzó, körző, szögmérő, toll, ceruza.

A vizsga két jól elkülöníthető részből áll.

I. rész (45 perc, 30 pont)

Ez a rész 10-12 feladatból áll, amelyek helyes megoldásához leginkább az alapfogalmak, definíciók, egyszerű összefüggések ismerete szükséges. A feladatok megoldásának sorrendje tetszőleges, és a legtöbb esetben a feladat megoldásához nem szükséges levezetés, ahol igen, ott ezt külön utasítással közlik. Ha nincs ilyen, akkor csak a megoldást kell egyértelműen megadni a megadott helyen. A 45 perc leteltével az I. részt a felügyelőtanár beszedi, ezt követően módosításra már nincs lehetőség.

II. rész (135 perc, 70 pont)

A második rész további két egységre bontható.

2A – Az itt található 3 feladat megoldása kötelező.

2B – Az itt található három feladat közül az egyik feladat kihagyható. A kihagyott feladat sorszámát meg kell adni a feladatlap megfelelő helyén! Ha ezt valaki elmulasztja vagy mind a három feladatot megoldja, akkor az utolsó feladatot tekinti a kihagyott feladatnak a javító tanár!

Ebben a részben a feladat megoldása során minden egyes lépést rögzíteni kell, világosan látsszon az alkalmazott gondolatmenet, és mindenképpen törekedni kell arra, hogy a résszámítások is nyomon követhetőek legyenek, hiszen az értékelés során így lehet pontosan javítani. Ha a végeredmény nem egyezik meg a megoldási útmutatóban megadottal, akkor sem kell kétségbe esni, hiszen részpontszámok is szerezhetőek! Ha több megoldás is készül, akkor egyértelműen jelölni kell, hogy melyik helyes!

MATEMATIKA ÉRETTSÉGI május 6. EMELT SZINT I

1 1) MATEMATIKA ÉRETTSÉGI 014. május 6. EMELT SZINT I. a) Egy téglalapt 70 darab egybevágó kis téglal.

Recommend Documents

MATEMATIKA ÉRETTSÉGI 2014. május 6. EMELT SZINT I. 1) a) Egy téglalapot 720 darab egybevágó kis téglalapra daraboltunk szét. A kis téglalapok oldalai közül az egyik 1 cm-rel hosszabb, mint a másik. Hány cm hosszúak egy-egy kis téglalap oldalai, ha a nagy téglalap területe 2025 cm2? (7 pont) b) Az 1, 2, 3, 4, 5, 6 számjegyekből összesen 720 olyan hatjegyű szám képezhető, melynek számjegyei között nincsenek egyenlők. Ezek között hány 12-vel osztható van? (5 pont) Megoldás: a)

Egy kis téglalap oldalainak hossza x cm, illetve x   x  1 cm2 . A feladat szövegéből kiindulva: 720  x   x  1  2025 .

x  1 cm, területe (1 pont) (1 pont)

A zárójelet felbontva, majd 45-tel leegyszerűsítve:

16x 2  16x  45  0

(1 pont) A két gyöke x-nek: x1  1,25; x2  2,25 . (1 pont) A negatív gyök nem lehet megoldása a feladatnak! (1 pont) A téglalap rövidebb oldala tehát 1,25 cm, hosszabb oldala pedig 2,25 cm hosszú. (1 pont) Ellenőrzés: 720  1,25  2,25  2025 igaz, tehát a válasz helyes. (1 pont) b) 12-vel azok a természetes számok oszthatók, amelyek 3-mal és 4-gyel is oszthatók. (1 pont) Mivel 1  2  3  4  5  6  21, ezért mind a 720 különböző hatjegyű szám osztható 3-mal. (1 pont) Azok a hatjegyű számok oszthatók 4-gyel, amelyeknél az utolsó két számjegy 12, 16, 24, 32, 36, 52, 56 vagy 64. (1 pont) Mindegyik végződés 4!, azaz 24 darab hatjegyű szám esetében fordul elő. (1 pont) Emiatt a vizsgált számok között 8  24  192 darab 12-vel osztható van. (1 pont) Összesen: 12 pont

2) Jelölje H a 5, 2  x  3 egyenlőtlenség pozitív egész megoldásainak halmazát. Jelölje továbbá B azon pozitív egész b számok halmazát, amelyekre a logb 26 kifejezés értéke is pozitív egész szám. Elemeinek felsorolásával adja meg a H, a B, a H  B és a B \ H halmazt! (11 pont) Megoldás: A gyökös kifejezés értelmezési tartomány vizsgálata alapján: x  5,2 . (1 pont) Az egyenlőtlenség elvégzése során: (1 pont) 5,2  x  9  3,8  x Tehát azok a pozitív számok elemei H halmaznak, melyek 3,8 -nál nagyobbak és 5,2-nél kisebbek: (1 pont) H  1; 2; 3; 4; 5 Ha logb 26  k , akkor bk  26 , ami 64. (2 pont) A k kitevő pozitív egész, ezért a b olyan pozitív egész szám lehet, melynek valamely pozitív egész kitevős hatványa 64-gyel egyenlő: (1 pont) 6 3 2 1 (2 pont) 2  4  8  64  64 Ezért B  2; 4; 8; 64 . (1 pont) H  B  2; 4

(1 pont) Összesen: 11 pont

3) Egy cég a függőleges irány kijelölésére alkalmas, az építkezéseknél is gyakran használt „függőónt” gyárt, amelynek nehezéke egy acélból készült test. Ez a test egy 2 cm oldalhosszúságú szabályos ötszög egyik szimmetriatengelye körüli forgatásával származtatható (lásd az ábrán). a) Hány cm3 a nehezék térfogata? Válaszát egy tizedesjegyre kerekítve adja meg! (9 pont) A minőség-ellenőrzés 120 darab 0,35 terméket vizsgált meg. 0,3 Feljegyezték az egyes darabok 0,25 egész grammokra kerekített 0,2 0,15 tömegét is. Hatféle tömeg fordult 0,1 elő, ezek relatív gyakoriságát 0,05 mutatja az oszlopdiagram. 0

b) Készítsen gyakorisági táblázatot a 120 adatról, és számítsa ki ezek átlagát és szórását! (5 pont)

A nehezék térfogata egy forgáskúp és egy csonkakúp térfogatának összege. (1 pont) A forgáskúp magassága az AFB derékszögű háromszögből: m  2  cos 54o (2 pont) A kúp alapkörének sugara: r  2  sin54o (1 pont) A csonkakúp h magassága a CGD derékszögű háromszögből: h  2  sin72o (2 pont) A forgáskúp térfogata:

A csonkakúp térfogata: 1,90   Vcsonkakúp   1,622  1,62  1  12 3 (1 pont) A nehezék térfogata a kettő összege: Vkúp  Vcsonkakúp  3,24  10,39  13, 6 (cm3).

b) A gyakorisági táblázat: tömeg (gramm) gyakoriság

A 120 adat átlaga: 12  105  . 6  110  107 (gramm). 120 A 120 adat szórása:

12  105  107   . 6  110  107   1,7  1, 3 (gramm). 120 2

(2 pont) Összesen: 14 pont

4) a) Deriváltfüggvényének

f  x   x  1,5x  6x függvényt a következő szempontok szerint: növekedés és fogyás, lokális szélsőértékek helye és értéke! (10 pont) b) Adja meg azt a g : 2; 3  függvényt, amelyre igaz, hogy g   f 3

(tehát az f függvény a g deriváltfüggvénye) és ezen kívül g  2  0 is teljesül! (4 pont)

Az f deriváltfüggvénye: ( f : 2;3  ) f   x   3x 2  3x  6 .

(1 pont) f  zérushelyei: -1 és 2. Az f  másodfokú függvény főegyütthatója pozitív, ezért f  értékei x  1 esetén pozitívak, 1  x  2 esetén negatívak, 2  x esetén pozitívak. Az f függvény menete ezek alapján: a 2; 1 intervallumon (szigorúan monoton) növekvő; az x  1 helyen (lokális) maximuma van, amelynek értéke 3,5; a  1; 2 intervallumon (szigorúan monoton) csökkenő; az x  2 helyen (lokális) minimuma van, amelynek értéke 10 ; a  2; 3 intervallumon (szigorúan monoton) növekvő. x

1  x  2 f  x   0

minimum f  2  10

maximum f  1  3,5

b) Mivel g az f-nek egyik primitív függvénye: x4 x3 g x     3x 2  c c   . 4 2 Mivel g  2  4  4  12  c  0 , ezért c  12 , és így g  x  

(1 pont) pont) pont) pont) pont) pont) pont) pont)

(1 pont) (1 pont) (1 pont)

x x   3x 2  12 4 2

(1 pont) Összesen: 14 pont

II. 5)  1 a) Igazolja, hogy a    , a 0 és a 3 is gyöke a 2x 3  5x 2  3x  0  2 egyenletnek, és az egyenletnek ezeken kívül más valós gyöke nincs! (5 pont) b) Oldja meg az alábbi egyenletet a valós számok halmazán! (6 pont) 2 cos3 x  5cos2 x  3 cos x  0 x x x c) Mutassa meg, hogy a 2  8  7  4  3  2  0 egyenletnek nincs valós gyöke! (5 pont)

2x 3  5x 2  3x  x 2x 2  5x  3  0

Egy szorzat akkor és csak akkor nulla, ha valamelyik tényezője nulla! Az x  0 valóban gyök. (1 pont) A többi gyököt a megmaradt másodfokú egyenletből kapjuk meg: 2x 2  5x  3  0 (1 pont) 1 A két gyök:  és 3 , azaz a megadott három szám valóban gyöke az eredeti 2 egyenletnek. (1 pont) Másodfokú egyenletnek legfeljebb két különböző valós gyöke lehet, ezért több gyök nincsen. (1 pont) b) Vezessünk be új ismeretlent: y  cos x !

A 2y 3  5y 2  3y  0 egyenletnek keressük a valós gyökeit, melyeket az a) 1 feladatrészből tudhatunk is: y1  0, y2   , y3  3 . (1 pont) 2 Mivel a cos x kifejezés értéke 1 és 1 között mozoghat csak, ezért a 3 nem jó megoldás. (1 pont)  A cos x  0 egyenlet megoldása: x1   k  , ahol k  (2 pont) 2 2 1  2m  , ahol m  A cos x   egyenlet megoldásai: x 2,3   (2 pont) 3 2 Az egyenlet bal oldalán 2x kiemelhető: 2x  2  4x  7  2x  3  0 . (1 pont)

Az exponenciális függvény értékkészlete a pozitív valós számok halmaza, így 2x  0 nem lehetséges. (1 pont) Másodfokúra visszavezethető a megmaradt egyenlet:

1 . (1 pont) 2 Az exponenciális függvény már említett értékkészlete miatt ezek nem valós gyökei, így valóban nincs megoldása az egyenletnek. (1 pont) 2x  3 vagy 2x  

Összesen: 16 pont

6) Egy üzemben olyan digitális műszert gyártanak, amely kétféle adat mérésére alkalmas: távolságot és szöget lehet vele meghatározni. A gyártósor meghibásodott, de ezt hosszabb ideig nem vették észre. Ezalatt sok mérőeszközt gyártottak, ám ezeknek csak a 93%-a adja meg hibátlanul a szöget, a 95%-a méri hibátlanul a távolságot, sőt a gyártott mérőeszközök 2%-a mindkét adatot hibásan határozza meg. a) Az egyik minőségellenőr 20 darab műszert vizsgál meg visszatevéses mintavétellel a meghibásodási időszak alatt készült termékek közül. Mekkora annak a valószínűsége, hogy legfeljebb 2 darab hibásat talál közöttük? (Egy műszert hibásnak tekintünk, ha akár a szöget, akár a távolságot hibásan méri.) (7 pont) Vízszintes, sík terepen futó patak túlpartján álló fa magasságát kell meghatároznunk. A síkra merőlegesen álló fát megközelíteni nem tudjuk, de van egy kisméretű, digitális műszerünk, amellyel szöget és távolságot is pontosan tudunk mérni. A patakparton kitűzzük az A és B pontokat, amelyek 10 méterre vannak egymástól. Az A pontból 55o -os, a B-ből 60o -os emelkedési szög alatt látszik a fa teteje. Szögméréssel még megállapítjuk, hogy ATB  90o , ahol T a fa „talppontja”. b) Milyen magas a fa? (9 pont) Megoldás: a)

A műszerek 7%-a hibásan méri a szöget, 5%-a pedig hibásan méri a távolságot. (1 pont) Mivel a műszerek 2%-a mindkét adatot hibásan méri, ezért a hibás műszerek aránya: 5  7  2  10 %. (1 pont) Egy hibátlan műszer választásának valószínűsége tehát 0,9. (1 pont) Akkor lesz köztük legfeljebb 2 hibás, ha a hibás műszerek száma 0, 1 vagy 2. (1 pont) Annak a valószínűsége tehát, hogy a 20 kiválasztott műszer között legfeljebb  20   20  2 hibás lesz: 0,920     0,919  0,1     0,918  0,12 . (2 pont)  1   2 A kérdezett valószínűség megközelítőleg 0,677. (1 pont) b) Jó ábra felrajzolása (2 pont) h Az ATP háromszögből: AT   0,700h (1 pont) tg55o h A BTP háromszögből: BT   0,577h (1 pont) tg60o Az ATB derékszögű háromszögből Pitagorasz-tétellel adódik: (1 pont) 2 2 h h (1 pont)  2 o  100 , 2 o tg 55 tg 60 Innen h  11 . (2 pont) A fa magassága tehát körülbelül 11 méter. (1 pont) Összesen: 16 pont

7) Egy növekvő számtani sorozat első három tagjából álló adathalmaz szórásnégyzete 6. a) Igazolja, hogy a sorozat differenciája 3-mal egyenlő! (4 pont) András, Barbara, Cili, Dezső és Edit rokonok. Cili 3 évvel idősebb Barbaránál, Dezső 6 évvel fiatalabb Barbaránál, Edit pedig 9 évvel idősebb Cilinél. Dezső, Barbara és Edit életkora (ebben a sorrendben) egy mértani sorozat három egymást követő tagja, András, Barbara és Cili életkora (ebben a sorrendben) egy számtani sorozat három szomszédos tagja. b) Hány éves András? (6 pont) András, Barbara, Cili, Dezső, Edit és Feri moziba mennek. c) Hányféleképpen foglalhatnak helyet hat egymás melletti széken úgy, hogy a három lány ne három egymás melletti széken üljön? (6 pont) Megoldás: a)

Ha a sorozat második tagját a2-nek jelöljük, akkor az első három tag átlaga is a2. (1 pont) Ha a számtani sorozat differenciáját d-nek jelöljük, akkor a szórásnégyzet:

a2  d  a2 2  02  a2  d  a2 2

(1 pont)  6. 3 Innen adódik, hogy d 2  9 , (1 pont) azaz, mivel a sorozatunk növekedő d  3 . Ezzel az állítást beláttuk. (1 pont) b) Ha Barbara x éves, akkor Cili x  3 éves, és így Dezső, Barbara és Edit életkora rendre x  6 , x, illetve x 12 év. (1 pont) Mivel ez a három szám egy mértani sorozat három szomszédos tagja, ezért: (1 pont)  x  6 x  12  x 2.

A zárójeleket felbontva: (1 pont) x 2  6x  72  x 2 , ahonnan x  12 . (1 pont) Ellenőrzés: Dezső, Barbara és Edit életkora 6, 12, illetve 24 év, ez a három szám pedig valóban egy mértani sorozat három szomszédos tagja. (1 pont) András tehát 9 éves. (1 pont) Komplementer eseményt felhasználva: nem felelnek meg azok az esetek, amelyekben a három lány három egymás melletti széken ül. (1 pont) A három egymás melletti széket négyféleképpen lehet kiválasztani a hat közül. (1 pont) A három egymás melletti széken 3!, azaz hatféleképpen foglalhat helyet a három lány, a megmaradt három helyen szintén hatféleképpen foglalhat helyet a három fiú. (1 pont) A nem megfelelő elhelyezkedések száma tehát: 4  6  6  144 . (1 pont) Hatan a hat egymás melletti székre 6!, azaz 720-féleképpen ülhetnének le. (1 pont) A megfelelő elhelyezkedések száma tehát: 720  144  576 . (1 pont) Összesen: 16 pont

8) Egy ABCD négyzet A csúcsa a koordinátarendszer y tengelyére, szomszédos B csúcsa pedig a koordinátarendszer x tengelyére illeszkedik. a) Bizonyítsa be, hogy a négyzet K középpontjának koordinátái vagy egyenlők, vagy egymás ellentettjei! (8 pont) b) Egy ilyen négyzet középpontja a  7; 7  pont. A négyzet oldala 10 egység hosszú. Számítsa ki a négyzet koordinátatengelyekre illeszkedő két csúcsának koordinátáit! (8 pont) Megoldás: a)

Legyen A  0; a  és B b;0  (de a 2  b2  0 ).

b a  Ekkor az AB szakasz felezőpontja F  ;  . (1 pont) 2 2 b a  Ebből adódóan FB  ;   . (1 pont) 2 2 Ha a négyzet középpontja a K pont, akkor FK az FB 90o -os vagy 90o -os elforgatottja. (1 pont)  a b a b  Tehát FK  ;  vagy FB   ;   . (1 pont)  2 2  2 2 Az F pont helyvektorát jelölje f, ekkor a K pont helyvektora k  f  FK , azaz a b a b  b a a b  k ; ; (2 pont) .  vagy k  2  2   2  2 Tehát a K középpont koordinátái valóban vagy egyenlők, vagy egymás ellentettjei. (1 pont) b) A négyzet körülírt körének sugara az átló fele, azaz 5 2 . (1 pont) A körülírt kör egyenlete:  x  7   y  7   50 . 2

A kör y tengelyen lévő pontjait x  0 helyettesítéssel, az x tengelyen lévő pontjait az y  0 helyettesítéssel adódó egyenlet adja meg. (1 pont) A kapott két egyenlet így: (1 pont) y  7 2  1 , illetve  x  7 2  1 . Ezeknek a megoldásai: y1  6 és y2  8 , illetve x1  6 és x 2  8 . Tehát a tengelyeken négy pont lehet a négyzet valamelyik csúcsa:  0;6 , 0;8 , 6;0 , 8;0 .

Figyelembe véve, hogy két szomszédos csúcs távolsága 10 egység két megoldás adódik: A1  0;6  , B1  8; 0  , illetve A2  0;8 , B2  6; 0  . (2 pont) Összesen: 16 pont

9) Kovács úr a tetőterébe egy téglatest alakú beépített szekrényt készíttet. Két vázlatot rajzolt a terveiről az asztalosnak, és ezeken feltüntette a tetőtér megfelelő adatait is. Az első vázlat „térhatású”, a második pedig elölnézetben ábrázolja a szekrényt.

A tetőtér adottságai miatt a szekrény mélységének pontosan 60 cm-nek kell lennie. a) Mekkora legyen a szekrény vízszintes és függőleges mérete (azaz a szélessége és a magassága), ha a lehető legnagyobb térfogatú szekrényt szeretné elkészíttetni? (A magasság, a szélesség és a mélység a szekrény külső méretei, Kovács úr ezekkel számítja ki a térfogatot.) (8 pont) A szekrény elkészült. Az akasztós részébe Kovács úr vasárnap este 7 inget tesz be, a hét minden napjára egyet-egyet. Az ingek között van 2 fehér, 2 világoskék és 3 sárga. Reggelente nagyon siet, ezért Kovács úr csak benyúl a szekrénybe, és anélkül, hogy odanézne, véletlenszerűen kivesz egy inget. b) Mennyi a valószínűsége annak, hogy a hét első három napján vagy három különböző színű vagy három egyforma színű inget választ? (Ha valamelyik nap viselt egy inget, azt utána már nem teszi vissza a szekrénybe.) (8 pont) Megoldás: a)

Ha a szekrény magassága x méter, akkor szélessége az ábrán látható egyenlő szárú háromszögek miatt 4 2  2x . (2 pont)

A térfogata pedig: V  0,6x 4 2  2x , amennyiben 0  x  2 2 . Az

(1 pont) másodfokú

függvénynek két zérushelye van, a 0 és a 2 2 . (1 pont) Így a negatív főegyüttható miatt ennek a függvénynek a maximuma a két zérushelye számtani közepénél, az x  2 helyen lesz. (2 pont) Mivel a 2 eleme a feladat értelmezési tartományának, ezért a legnagyobb térfogatú szekrény magassága körülbelül 1,41 méter, szélessége pedig körülbelül 2,83 méter lesz. (2 pont)

b) Az azonos színű ingeket megkülönböztetve az első három napon 7  6  5  210 különböző lehetőség van a három ing kiválasztására. (1 pont) Kedvező esemény az, ha valamilyen sorrendben mindegyik színből pontosan egyet vagy három sárga inget választott Kovács úr. (1 pont) Egy adott színsorrendben 2  2  3  12 különböző módon lehet három inget kiválasztani. (1 pont) Három adott szín sorrendje 3!-féle lehet, tehát három különböző színű inget 2  2  3  3!  72 különböző módon választhat ki Kovács úr. (2 pont) A három sárga inget 3! különböző sorrendben választhatja ki. (1 pont) A kedvező esetek száma: 2  2  3  3! 3!  78 . (1 pont) A kérdezett valószínűség tehát: 78 13 (1 pont)   0, 371 . 210 35 Összesen: 16 pont