Sokszínű Matematika 7 2 csillagozás
A harmadik és a negyedik ábra alapján a középső tartomány értéke pont.
Régi tankönyvek – Egyéb középiskolai könyvek
Mi befolyásolhatja a hirdetések sorrendjét a listaoldalon?
A hirdetések sorrendjét a listaoldalak tetején található rendezési lehetőségek közül választhatod ki, azonban bármilyen rendezési módot választasz ki, a lista elején mindig azok a szponzorált hirdetések jelennek meg, amelyek rendelkeznek a Listázások elejére vagy a Maximum csomag termékkiemeléssel. Ezeket a lista elején található Kiemelt ajánlatok sáv jelöli.
Termékkiemeléseinket termékfeltöltés során, a Hirdetés kiemelése oldalon tudod megrendelni, de természetesen arra is lehetőség van, hogy már futó hirdetéseidhez add hozzá azokat.
A kiemelésekről ITT, a rendezési lehetőségekről ITT olvashatsz részletesebben.
Sokszínű Matematika 7 2 csillagozás

Az elmúlt évek legnépszerűbb és legszínvonalasabb matematika-tankönyvcsaládjának tagja. Az iskolai oktatásban, valamint otthoni gyakorlásra továbbra is kitűnően használható.
A tankönyvcsalád felsőbb évfolyamos köteteire is jellemző, hogy a tananyag feldolgozásmódja tekintettel van a tanulók életkori sajátosságaira. Ezért bár nem siettetik az absztrakt eszközök bevezetését, a 7. és 8. osztályos tananyagban már sor kerül a definíciók alkalmazására, a bizonyítási igény kialakítására is.
A kidolgozott példák segítik az önálló tanulást és megértést.
Eredeti megjelenés éve: 2008

Mozaik, Szeged, 2019

Mozaik, Szeged, 2014

Mozaik, Szeged, 2012

Mozaik, Szeged, 2012

Mozaik, Szeged, 2008
Most olvassa 2



Kiemelt értékelések


Jakab Tamás – Kosztolányi József – Pintér Klára – Vincze István: Sokszínű Matematika 7
A hetedikes tankönyv újdonsága a bevezetés a halmazelméletbe és a függvénytanba. Megismerkedünk a számtani sorozat fogalmával, és jobban elmélyülhetünk a statisztika és valószínűség témájában. Megtudjuk, mit jelent a medián és a módusz.
A geometriai ismeretek is tovább bővülnek a hatodikos könyvhöz (http://moly.hu/ertekelesek/1245966) képest. Az erre vonatkozó részek nem hoztak lázba.
Az efféle nyelvi hibákra lehetett volna jobban ügyelni:
Gáborék hosszú autós kirándulásra mentek.
Nyilván a kirándulás lehetett hosszú, nem pedig az autó, így azonban, vessző nélkül, az utóbbiról van szó.
Erre a könyvre is jellemzők a szép, színes, kedves rajzok.

Mozaik, Szeged, 2008


Jakab Tamás – Kosztolányi József – Pintér Klára – Vincze István: Sokszínű Matematika 7
Én szeretem ezt a matek könyvet, segít, hogy a matekot is elviseljem. A szerkesztéshez lenne egy-két javaslatom (pl. miért kell, csak úgy mellékesen apró betűvel az oldal szélére lökni fontos szabályt vagy olyan logikai lépést, amivel könnyebben megérthető egy – egy matematikai probléma).
Hatodikos matematika tankönyv

Rendelése leadásához lépjen be felhasználói fiókjába vagy regisztráljon oldalunkra!



Fenyős Zoltán-Fenyősné Kircsi Amália
PD-442 – Hatodikos informatika tankönyv
136 oldal | 165 mm x 230 mm | 220 g
A hatodikos korosztály nyelvi fejlettségéhez igazodó, olvasmányos tankönyv a gyakorlatot állítja a középpontba. A kerettanterv [51/2012. (XII. 21.) EMMI rendelet 2. sz. melléklet] témakörei közül a következőket tárgyalja: informatikai eszközök használata, dokumentumkészítés, problémamegoldás, infokommunikáció, könyvtárhasználat. Ennek megfelelően a leckék is 5 fejezetbe rendeződnek. Az ismeretek átadásában kulcsszerepet játszanak a feladatok, amelyek életszerűek, praktikus szemléletet közvetítenek, a tanulók saját tapasztalatait is előhívják, tehát maradandóbb tudást eredményeznek. A tankönyv a kötelező és az emelt óraszámú oktatásban egyaránt jól alkalmazható.
Az új állami biológia tankönyv szerint “a fiúk és a lányok bizonyos szellemi képességekben különbözőek”

Tudta, hogy a matematikában a fiúk ügyesebbek? Nem? Akkor olvasson bele a 6. osztályosoknak készült állami természetismeret könyvbe, és jegyezze meg, hogy ez a helyzet! Persze a matek csak egy példa a sok közül,
“Hiszen a fiúk és lányok bizonyos testi adottságokban és szellemi képességekben különbözőek.”
Vannak példák is, hogy a gyerekek nehogy úgy érezzék, hogy a könyvben mindenféle alap nélkül írnak le ostobaságokat. Így például kiderül, hogy
- a fiúk jobbak bizonyos sportokban,
- a lányok viszont kézügyesebbek,
- a lányok állítólag (tényleg oda van írva a könyvben, hogy állítólag) könnyebben tanulnak olvasni,
- a fiúk viszont (nem állítólag) matematikában ügyesebbek.
Az is kiderül, hogy
a lányok máshogy nyilvánítják ki az érzelmeiket, mint a fiúk.
A könyv a gyerekek viselkedését elemzve azt is megállapítja, hogy
a lányok jól érzik magukat anyaszerepben, feleség szerepében, a fiúk pedig apaszerepben, a férj szerepében.
Nem vagyunk egyformák, na.
A fiúk és a lányok matematikai képességei közötti különbséggel több kutatás is foglalkozott. Meg fognak lepődni, de egyáltalán nem az jött ki, hogy a fiúk ügyesebbek matematikában. Van olyan teszt, amin jobban teljesítenek, de ennek kb. egymillió oka lehet a biológián kívül.
Az egyik például az, hogy a világon sok helyen a lányok már egész kiskoruktól azt hallgatják, hogy ők matekból gyengébbek.
És hát az egész könyvvel pont ez a probléma.

Az egyetemekre több lány (pl) kerül be, mint fiú, a gazdaságban, vagy a közéletben mégis a férfi vezetők vannak többségben. Részben pont azért, mert a lányok önbizalmát nem hogy erősíti, hanem durván gyengíti az oktatási rendszer. Aki kiskorától azt hallja, hogy neki különböző szellemi képességei vannak, és hogy hát például matekban is a fiúk ügyesebbek, abból kevésbé valószínű, hogy felsővezető lesz egy banknál. Vagy bárhol.
Valamivel egyébként jobban jár, aki nem az állami Nemzedékek Kiadó tankönyvéből, hanem az állami Oktatáskutató és Fejlesztő Intézet kísérleti tankönyvéből tanul 6. osztályban természetismeretet. Abban szellemi különbségekről nincs szó, csak arról, hogy a
Úton az egyenletek használata felé
Január a középiskolai írásbeli felvételik ideje. Gyermekünk, unokánk, távolabbi rokonunk vagy ismerőseink egyike-másika felvételizik. Hallunk azokról a feladatokról, amelyek kihívást jelentettek számukra.
Előfordulhat, hogy megkérnek, segítsünk a vizsgára való felkészülésben. Az első, hogy megismerkedjünk az elmúlt évek felvételi követelményeivel. Szerencsére 2001 óta a feladatsorok elérhetőek az Oktatási Hivatal honlapján:
Az Érintő 2021. márciusi számában olvashatunk a tavalyi nyolcosztályos, hatosztályos és négyosztályos gimnáziumi felvételik általános értékeléséről.
A hatosztályos gimnáziumok felvételi anyagait tanulmányozva láthatjuk, hogy minden évben előfordulnak olyan szöveges feladatok, amelyeket felnőttként ösztönösen egyenlettel oldanánk meg. Milyen eszközei vannak a hatodik osztályos gyerekeknek ilyen problémák megoldására? A korábbi években a betűs kifejezések használata, nyitott mondatok, egyszerű egyenletek megoldása a hatodik évfolyam második felében szerepelt, tehát már akkor is a felvételi időszak után. Az új NAT bevezetésével ezek a módszerek későbbi évfolyamokra kerültek. Tehát ma az egyenletmegoldás nem a 12 éves diákoktól elvárt rutin. Ők vajon hogyan birkóznak meg a szöveges feladatokkal, mennyire tudnak betűket használni az összefüggések leírására? Logikai következtetéseket használnak? Esetleg egyenletmegoldási módszerekhez hasonlót alkalmaznak? Megfogalmazva a fő kérdést: Tanítsuk meg nekik az egyenletek megoldásának néhány szokásos módszerét a felvételire készülve?
A Kempelen Farkas Gimnázium hatodikos diákjainak feladtunk 8 olyan példát, amelyek az előző 10 év valamelyikében felvételi feladatok voltak. Bizonyos feladatokat órán, másokat otthon oldottak meg szorgalmi feladatként. Az órán egyénileg dolgoztak, otthon több idejük volt a megoldásra, esetleg szülői segítséget is kaphattak. Azt kértük tőlük, hogy megoldásaikat indokolják is, ellentétben a központi írásbeli feladatok követelményeivel, ahol csak a végeredményt kell megadniuk, a javítási útmutató általában ezt értékeli.
Az alábbiakban bemutatunk néhány megoldást a diákok munkáiból. Elemezzük gondolkodásmódjuk sajátosságait, értékeit. Javaslatokat teszünk arra, hogy a felvételi rendszerétől függetlenül a mindennapi tanítási gyakorlatban milyen módszerek megismertetését ajánljuk ebben az életkorban.
Ezeket a feladatokat tanárszakos hallgatók is megoldották, – természetesen egyenlettel – de kérésre adtak más típusú megoldásokat is. Erről is beszámolunk a cikk végén.
A tankönyvek is változatos módszereket kínálnak a szöveges feladatok megoldására, ezekre a tankönyvekre is utalunk a befejezésben.
A feladatokra a kitűzés dátumával és a feladatsorban elfoglalt sorszámukkal fogunk hivatkozni. A megoldásokat nem szó szerint idézzük. A 12 éves gyerek megoldásában sokszor meg kell érezni a mögötte lévő gondolatot, amit esetleg még nem tud korrekt módon szavakba önteni. A cikk olvasója számára érthető formára hoztuk, eközben figyeltünk arra, hogy ne hamisítsuk meg a benne lévő eredeti gondolatot – több feladat esetében a diákmunka fotóját is megadtuk. Többféle megoldás született mindegyik feladat, feladatrész esetében. Megadtuk a feladat megoldását egyenlet alkalmazása nélkül és egyenlet használatával is.
1. (2022. január 22. – 9. feladat)
Anna és Berci lemérte egy téglalap alakú kert három szomszédos oldala hosszának összegét. Az Anna által lemért oldalak hosszának összege 72 méter, a Berci által lemért oldalak hosszának összege 75 méter.
a) Hány méterrel hosszabb a kert hosszabb oldala a rövidebbnél?
b) Hány méter a kert rövidebb oldalának hossza?
c) Hány méter a kert kerülete?
d) Hány négyzetméter a kert területe?
Egy megoldás következtetéssel:
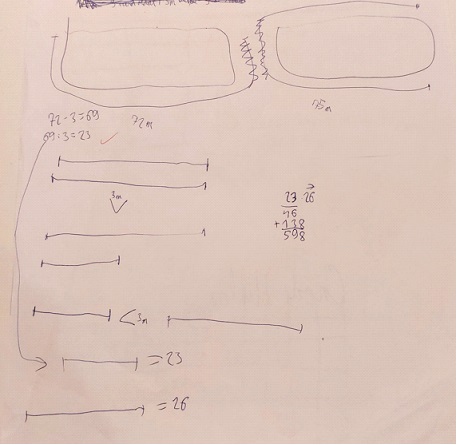
Ebből a leírásból ez a gondolatmenet olvasható ki:
A téglalap két oldala és :
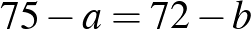
a) Ebből látható, hogy az oldal méterrel nagyobb -nél.
b) Ezért a rövidebb oldal háromszorosa, azaz (m).
c) A hosszabb oldal . A kerület (m)
d) A terület m
Sokan használtak betűket az összefüggések leírására. Néhányan eljutottak az egyenletrendszer megoldásáig is.
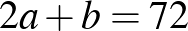
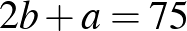
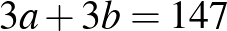
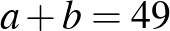
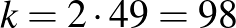
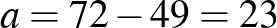
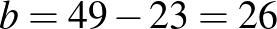
Kicsit „bonyolultabban”:
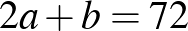
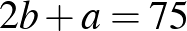
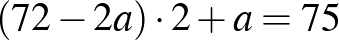
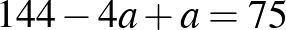
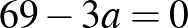
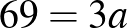
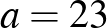
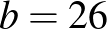
2 . (2020. január 18. – 8. feladat)
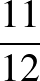
Ezt a megoldást így írhatjuk le a felnőttek nyelvén:
Hétfőn és kedden Hajni 66 feladatot oldott meg helyesen. Ez a feladatok $” height=”” /> része. Ekkor $” height=”” /> rész 6 feladat. Összesen feladattal foglalkozott.
| Hétfő | Hétfőn hibás | Kedd | Kedden hibás | Összesen |
| 12 | 1 | 6 | 0,5 | 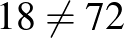 |
| 24 | 2 | 12 | 1 | 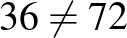 |
| 36 | 3 | 18 | 1,5 | 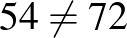 |
| 48 | 4 | 24 | 2 | 72 jó |
Ebből megadható a válasz a kérdésekre.
Következtethetünk
a) Hétfőn a feladatok $” height=”” /> részét megoldotta, $” height=”” /> részét pedig nem.
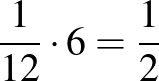
b) A 66 feladatot 2:1 arányban kell felosztani: , tehát 44 feladatot oldott meg helyesen hétfőn.
c) Kedden 22 feladatot oldott meg helyesen. Ez a feladatok $” height=”” /> része. Az $” height=”” /> rész , tehát kedden feladatot nem oldott meg helyesen.
Egyenlettel így dolgozhatunk:
Hétfőn feladat. Megoldva x, $” height=”” /> hibás x$” height=”” />.
Kedden x=\dfracx$” height=”” />. Megoldva \cdot \dfracx=\dfracx$” height=”” />.
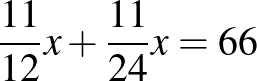
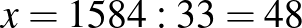
Ebből könnyen megkapjuk a feltett kérdésekre a válaszokat
Két ismeretlennel így jutunk eredményre:
hétfő: 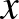 |
helyes 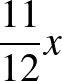 helytelen helytelen 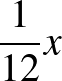 |
kedd: 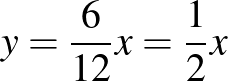 helyes helyes 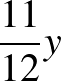 helytelen helytelen 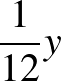 |
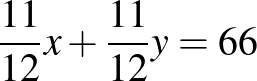
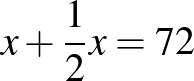
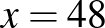
3. (2020. január 23. – 10. feladat)
Az osztály tanulói közül 12-en járnak matematika-szakkörre. 5-tel több fiú nem jár matematika-szakkörre, mint ahány lány jár. Ugyanannyi fiú jár matematika-szakkörre, mint ahány lány nem jár. A lányok közül 2-vel többen járnak matematika-szakkörre, mint ahányan nem járnak.
a) Hány lány jár az osztályba?
b) Hány fiú jár az osztályba?
c) Hány lány jár matematika-szakkörre?
Több jó megoldást találtunk a megoldások között minden indoklás nélkül. Azt tételezzük fel, hogy a gyerekek agyában a megoldáshoz vezető út összetettebb, mint amit ebben a korban meg tudnak fogalmazni. Ha ilyenkor például szakkörön rákérdezünk, akkor szóban körül tudják írni a gondolatmenetüket.
Ilyen gondolkodásra utal, amit ez a gyerek írt:

Láttunk egyenletrendszeres megoldást is:
fiú jár szakkörre, nem jár. Jár szakkörre, nem jár.
A feladat feltételei:
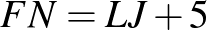
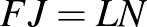
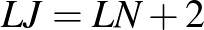
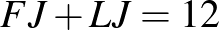
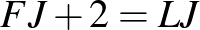
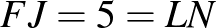
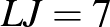
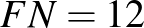
Ilyesmit mutat ez a munka:
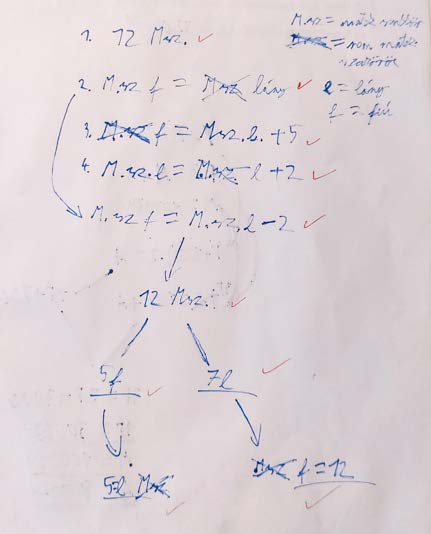
Van, aki találgat:
12 szakkörös van. Tudjuk, hogy több lány jár mint fiú. Ez ilyen felosztásban lehetséges:
| LJ | FJ |
| 11 | 1 |
| 10 | 2 |
| 9 | 3 |
| 8 | 4 |
| 7 | 5 |
Csak az utolsó sor adataival nem jutunk ellentmondásra:
; .
…és találkoztunk a felnőttes megoldással is (otthon született), feltételezzük, hogy szülői segítség van mögötte. Táblázatban foglaljuk össze, amit tudunk:
| Jár | Nem jár | |
| L | 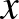 |
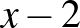 |
| F | 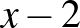 |
 |
| Össz | 12 |
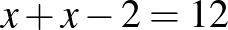
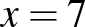
4. (2019. január 24. – 10. feladat)
Peti és az öccse, Marci egy könyvet vásároltak édesanyjuk születésnapjára az édesapjukkal közösen. A két gyerek együtt feleannyit fizetett, mint az édesapa. Peti harmadannyit fizetett, mint az öccse és az édesapja együtt. Marci 1000 Ft-ot fizetett.
a) Az édesapa hányadrészét fizette a könyv árának?
b) Peti hányadrészét fizette a könyv árának?
c) Hány forintot fizetett Peti?
d) Hány forintot fizetett az apa?
e) Hány forintba került a könyv?
A faladatot megoldhatjuk arányos következtetéssel:

A fenti megoldásban ez a gondolat:
Az apa $” height=”” /> -át, Peti $” height=”” /> -ét fizette a könyvnek.
Ha 60 Ft lenne a könyv ára, akkor Peti 15-öt, apa 40-et, Marci 5-öt fizetne. Marci 200-szor annyit, 1000 Ft-ot fizet, ezért Peti Ft-ot, apa Ft-ot fizetett.
A könyv ára így 12 000 Ft.
Van olyan diák, aki betűket használ és egyenletet old meg:
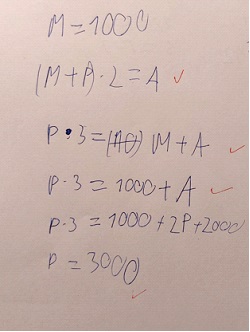
Petinek forintja, Marcinak forintja, édesapjuknak forintja volt: .
Tehát a könyv ára 12 000 Ft.
5. (2016. január 16. – 7. feladat)
Az ábrán négy egyforma céltábla látható. A céltáblákon a lövések helyét pöttyök jelölik. A céltáblák alá odaírtuk, hogy hány pontot érnek összesen a céltáblára érkezett lövések (lásd ábra).
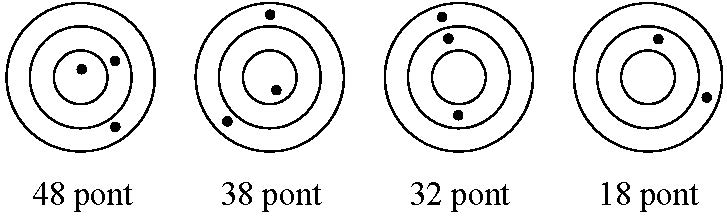
a) Hány pontot ér egy lövés, ha a legbelső körbe esik?
b) Hány pontot ér egy lövés, ha a legkülső sávba esik?
Következtetéssel:
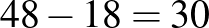
A harmadik és az utolsó ábra alapján a belső tartomány értéke pont.
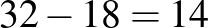
A harmadik és a negyedik ábra alapján a középső tartomány értéke pont.
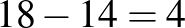
A negyedik ábra alapján a külső tartomány értéke pont.
Ezt a gondolatmenetet egyenletekkel is leírhatjuk:
A belső tartomány pont, a középső pont, a külső tartomány pont.
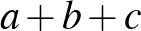 |
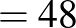 |
( 1 ) |
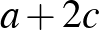 |
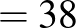 |
( 2 ) |
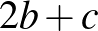 |
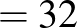 |
( 3 ) |
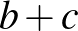 |
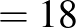 |
( 4 ) |
| (1) – (4) | 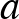 |
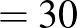 |
| (3) – (4) | 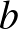 |
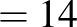 |
| (4) | 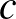 |
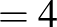 |
Ehhez hasonló gondolatmenetet találtunk ebben a megoldásban is:
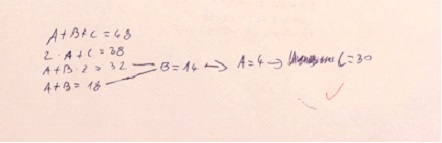
6. (2015. január 17. – 8. feladat)
Jancsi egy tábla csokoládét szeretne venni, de ehhez 60 Ft-ja hiányzik. Ezt a tábla csokit Sanyi sem tudja megvenni, mert 45 Ft-ja hiányzik hozzá. Együtt annyi pénzük van, hogy vehetnek egy ilyen tábla csokoládét, és még marad 10 Ft-juk.
a) Kinek van több pénze és mennyivel?
b) Hány forintba kerül egy tábla csokoládé?
c) Hány forintja van Sanyinak?
A diákok általában egyenletet használtak a megoldáshoz:
A csoki cs forintba kerül:
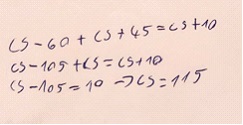
a) Sanyinak 15 forinttal több pénze van.
b) Egy csoki 115 forintba kerül.
c) Sanyinak 70 forintja van.
Ábrával és következtetéssel:
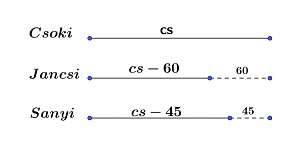
Jancsi pénzéhez Ft-ot kell adnunk, hogy a csoki áránál forinttal többet kapjunk, ezért Sanyinak Ft-ja van. Sanyi pénzéhez forintot kell adni, hogy a csoki áránál Ft-tal többet kapjuk, ezért Jancsinak 55 forintja van. A csoki forintba kerül.
7 . (2014. január 18. –10. feladat)
Dóri, Sári és Anna a legutóbbi, matematikából írt dolgozatukról beszélgettek. A dolgozatukra kapott pontszámaikról a következőket mondták:
Dóri: Hármunk pontjainak összege 258, és nem az enyém lett a legrosszabb hármunk közül.
Anna: Nem az enyém a legjobb, de három ponttal magasabb hármunk pontszámának átlagánál.
Sári: Kettőtök pontjainak összege 30-cal több az én pontszámom kétszeresénél.
a) Kinek lett legkevesebb pontja hármuk közül?
b) Hány pontot kapott a dolgozatára Anna?
c) Hány pontot kapott a dolgozatára Sári?
Hogyan értsük, ha ezt írja egy diák:
 lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” /> lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” /> |
 lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” /> lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” /> |
nem A |
| nem A |  lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” /> lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” /> |
 lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” /> lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” /> |
 lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” /> lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” /> |
 lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” /> lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” /> |
nem S |
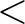
A nagyságrendet úgy írjuk le, hogy írunk két lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” /> jelet, és beillesztjük a megfelelő információt a megfelelő helyre.
A nem a legnagyobb: … $” height=”” /> … $” height=”” /> nem A (Mert Anna ezt állítja.)
A nem a legkisebb (Mert nagyobb az átlagnál.): nem A $” height=”” /> … $” height=”” /> … (Ebből már következik, hogy A a középső.)
S nem a legnagyobb: … $” height=”” /> … $” height=”” /> nem S (Mert S kisebb, mint A és D átlaga. Ebből már következik, hogy D a legnagyobb.)
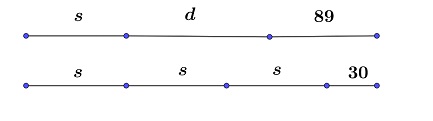
Ez alapján . Innen , .
8. (2014. január 23. – 7. feladat)
A könyvesbolt két egyforma hosszúságú polcára egyforma vastagságú mesekönyveket és egyforma vastagságú tankönyveket állítottunk egymás mellé. Az egyik polcot 20 mesekönyvvel és 15 tankönyvvel töltöttük ki, a másikat 12 mesekönyvvel és 27 tankönyvvel.
a) Hány tankönyv vastagsága egyenlő két mesekönyv vastagságával?
b) Hány mesekönyvvel tölthető ki a polc teljesen?
c) Hány centiméter vastag egy tankönyv, ha a polc hossza 90 cm?
Egy gondolat arra, hogy a mesekönyv a vastagabb:

Egy teljes, jó megoldás a gyerekek megoldásaiból összeállítható. De ez így együtt nem szerepelt a dolgozatokban:
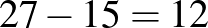
A második polcon tankönyvvel van több.
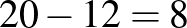
Az első polcon mesekönyvvel van több.
Ezért 12 tankönyv olyan vastag, mint 8 mesekönyv, tehát 3 tankönyv vastagsága egyenlő 2 mesekönyv vastagságával.
Az első polcon a tankönyvet mesekönyvre válthatjuk, ezért a polc szélessége mesekönyvvel vastagságával egyezik meg, egy mesekönyv 3 cm vastag. 2 mesekönyv 6 cm, tehát 1 tankönyv 2 cm vastag.
Comments are closed, but trackbacks and pingbacks are open.