Matematika felvételi 2022: ezek voltak a feladatok és megoldások

felét, kedden a maradék harmadát, szerdán a megmaradt pénze negyedét, és így 300 Ft-ja maradt. a) Mennyi pénze maradt keddről szerdára? . b) Mennyi pénze maradt hétfőről keddre? . c) Mennyi pénze volt eredetileg? . a b c 8. évfolyam – M–2 feladatlap / 4 7. A következő diagramon a XX. század utolsó négy olimpiáján szerzett magyar érmek számát ábrázoltuk (A: arany, E: ezüst, B: bronz). db Szöul 1988 Barcelona 1992 Atlanta 1996 Sydney 2000 A E B A E B A E B A E B 8 6 4 2 a) A négy közül melyik olimpián szereztük a legkevesebb ezüstérmet? . b) Összesen hány aranyérmet szereztünk ezen a négy olimpián? . c) Átlagosan hány ezüstérmet szereztünk ezen a négy olimpián? . d) Melyik fajta éremből szereztük összesen a legtöbbet ezen a négy olimpián? . a b c d 8. évfolyam – M–2 feladatlap / 5 8. Az ábrán látható háromszor hármas táblára olyan kockákat helyeztünk, amelyeknek a lapjai egybevágóak a

Központi felvételi 2022 megoldókulcs – hasznos infok itt!

A 9. évfolyamra történő beiskolázás központi írásbeli felvételi vizsgáinak feladatsorai és javítási-értékelési útmutatói a 2021/2022. tanévben.

Feladatlapok a 8. osztályosok számára (9. évfolyamra történő beiskolázás)

2022. január 22.

Feladatsor	Javítási-értékelési útmutató
Magyar nyelv	Magyar nyelv
Matematika	Matematika

Pótló írásbeli felvételi vizsga – 2022. január 27.

Feladatsor	Javítási-értékelési útmutató
Magyar nyelv	Magyar nyelv
Matematika	Matematika

Pótló írásbeli felvételi vizsga 2. nap – 2022. február 04.

Feladatsor	Javítási-értékelési útmutató
Magyar nyelv	Magyar nyelv
Matematika	Matematika

A dokumentumokat PDF állományok tartalmazzák, amelyek tartalomhű megjelenítést és nyomtatást tesznek lehetővé.

A PDF állományokban tárolt adatok megjelenítéséhez és nyomtatásához PDF olvasó program szükséges (pl. Adobe Reader, Sumatra PDF, Foxit Reader stb.).

Felvételi feladatsorok a 6 és 8 osztályos gimnáziumba – 2022

A 6 és 8 évfolyamos gimnáziumok központi írásbeli felvételi vizsgáinak feladatsorai és javítási-értékelési útmutatói a 2021/2022. tanévben.

Felvételi feladatsorok – 6 osztályos gimnáziumba

2022. január 22.

Feladatsor	Javítási-értékelési útmutató
Magyar nyelv	Magyar nyelv
Matematika	Matematika

Pótló írásbeli felvételi vizsga – 2022. január 27.

Feladatsor	Javítási-értékelési útmutató
Magyar nyelv	Magyar nyelv
Matematika	Matematika

Pótló írásbeli felvételi vizsga 2. nap – 2022. február 04.

Feladatsor	Javítási-értékelési útmutató
Magyar nyelv	Magyar nyelv
Matematika	Matematika

Felvételi feladatsorok – 8 osztályos gimnáziumba

2022. január 22.

Feladatsor	Javítási-értékelési útmutató
Magyar nyelv	Magyar nyelv
Matematika	Matematika

Pótló írásbeli felvételi vizsga – 2022. január 27.

Feladatsor	Javítási-értékelési útmutató
Magyar nyelv	Magyar nyelv
Matematika	Matematika

Pótló írásbeli felvételi vizsga 2. nap – 2022. február 04.

Feladatsor	Javítási-értékelési útmutató
Magyar nyelv	Magyar nyelv
Matematika	Matematika

A dokumentumokat PDF állományok tartalmazzák, amelyek tartalomhű megjelenítést és nyomtatást tesznek lehetővé. A PDF állományokban tárolt adatok megjelenítéséhez és nyomtatásához PDF olvasó program szükséges (pl. Adobe Reader, Sumatra PDF, Foxit Reader stb.).

Matematika felvételi 2022: ezek voltak a feladatok és megoldások!

Dancsó Imre, 2022. augusztus 17.

8. osztály: milyen feladatok voltak?

A nyolcadik osztályosok központi írásbeli felvételije senkinek nem okozott meglepetést. Ugyanazok a típusfeladatok voltak, mint az elmúlt években. Ezek ellenére még mindig nem könnyű jól teljesíteni, hiszen az idővel való versenyfutás is megmaradt az elmúlt évekből. Nézzük milyen típusok kerültek be a feladatsorba, mire kaptak a gyerekek 45 percet!

1. feladat: Könnyű számolási feladatok (az utolsónál le kellett írni a számolás menetét is)
2. feladat: Mértékegységváltás (idén tömeg, térfogat, hosszúság)
3. feladat: Logika puzzle (minden évben nehézség, hogy nem tudja a vizsgázó, hány megoldás van)
4. feladat: Grafikon elemzés
5. feladat: Szögek meghatározása ábra alapján (egyenlőszárú háromszögek)
6. feladat: Átlaghoz kapcsolódó nehezebb szöveges
7. feladat: Feleletválasztós feladatok (oszthatóság, százalék, szögek)
8. feladat: Táblázatkitöltés közepesen nehéz számolásokkal (egyenletmegoldás)
9. feladat:Térgeometria (felszínszámolás)
10. feladat: Nehéz szöveges feladat (százalékszámítással és törtekkel, egyenletmegoldás)

Nézzük részletesen a feladatokat megoldásokkal együtt!

Itt megtalálod a 2022-es matematika felvételi első 6 feladatát interaktív megoldásokkal, amikből rengeteget tanulhatsz
(Az interaktív megoldásokhoz jelentkezz be! Ha még nincs fiókod, akkor regisztrálj!

Hasonló interaktív videókon átnézhetsz minden matek felvételi témakört, és begyakorolhatod az felvételi feladatok megoldását!

Jöhet a többi feladat? Csináld meg velünk a 2022-es matematika felvételi 7-10. feladatát!

Nézd meg a videót és közben válaszolj a kérdésekre! (Lépj be, vagy regisztrálj.)

Hihetetlenül gyorsan tudsz készülni matekból a felvételire az egyedi módszereknek és a jól felépített tananyagnak köszönhetően:

Ezek voltak a 8.-os felvételi feladatok:

1. Határozd meg az A, B, C és D érékét!

a) A = 36 : (5 · 4)

b) B = 24 és 9 legkisebb közös többszöröse

c) C-nek a kétharmada 32

d-e) D = −
Írd le a számolás menetét is!

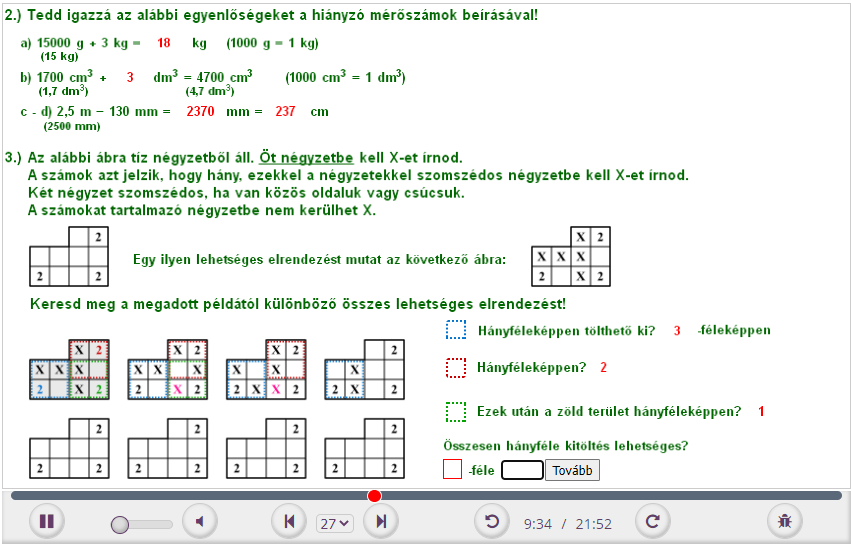
2. Tedd igazzá az alábbi egyenlőségeket a hiányzó mérőszámok beírásával!

a) 15 000 g + 3 kg = __________ kg

b) 1700 cm 3 + __________ dm 3 = 4700 cm 3

c-d) 2,5 m − 130 mm = __________ mm = __________ cm

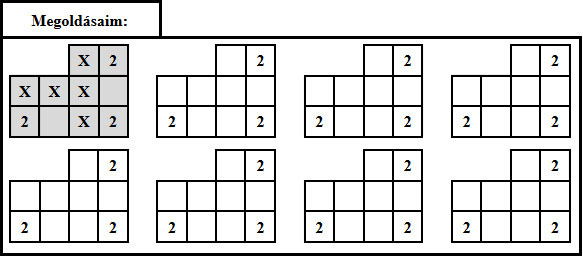
3. Az alábbi ábra tíz négyzetből áll. Öt négyzetbe kell X-et írnod.
A számok azt jelzik, hogy hány, ezekkel a négyzetekkel szomszédos négyzetbe kell X-et írnod.
Két négyzet szomszédos, ha van közös oldaluk vagy csúcsuk.
A számokat tartalmazó négyzetbe nem kerülhet X.

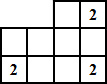
Egy ilyen lehetséges elrendezést mutat az alábbi ábra:

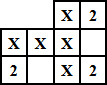
a) Keresd meg a megadott példától különböző összes lehetséges elrendezést!
Megoldásaidat a vastag vonallal körülvett részbe kell beírnod, mert csak ezt értékeljük. Lehet, hogy több üres ábrát adtunk, mint ahány megoldás van. A példaként megadott ábrát már beírtuk. A bekeretezett rész alatti területen próbálkozhatsz, de az oda beírt megoldásokat NEM értékeljük!
Vigyázz! Ha a megoldásaid közé hibás elrendezést is beírsz, pontot vonunk le.

4. Egy vasútmodell két mozdonya (A és B) két, egymással párhuzamosan lerakott sínen mozgott előre és hátra.

A két mozdony mozgását az alábbi grafikonon ábrázoltuk:

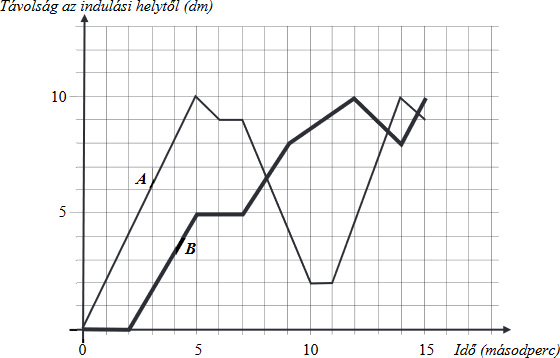
a) Hány alkalommal haladtak el egymás mellett a mozdonyok, ha az A mozdony elindulását nem tekintjük annak?

b) Hány másodpercig állt a B mozdony az ábrázolt időszak alatt?

c) Hány dm utat futott be összesen az A mozdony az ábrázolt időszak alatt?

d) Hány másodpercig közeledett az indulási ponthoz az A mozdony?

5. Az alábbi ábrán vázolt ABCD négyszög AD oldalán lévő P pont úgy helyezkedik el, hogy a CP
szakasz felezi a C csúcsnál lévő szöget, valamint CD = CP és PB = AB.
Az ábrán megadtuk két szög nagyságát.
(Az ábra csak tájékoztató jellegű vázlat, nem pontos méretű.)

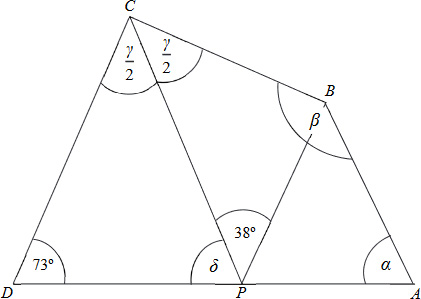
a) Mekkora a CDP háromszögben a P csúcsnál lévő δ szög nagysága?

b) Mekkora az ABP háromszögben az A csúcsnál lévő α szög nagysága?

c) Mekkora az ABCD négyszögben a C csúcsnál lévő γ szög nagysága?

d) Mekkora az ABCD négyszögben a B csúcsnál lévő β szög nagysága?

6. Tibi az első félévben összesen 15 érdemjegyet szerzett matematikából. Az érdemjegyek közül négy darab hármas volt, a többi négyes vagy ötös. Tibi 15 érdemjegyének átlaga 4,2 lett.

a) Hány ötöst kapott Tibi matematikából az első félévben?
Írd le a számolás menetét is!

7. Minden kérdés után karikázd be az egyetlen helyes válasz betűjelét!

a) Hány 0-ra végződik az 1 · 2 · 3 · 4 · 5 · 6 · 7 · 8 · 9 · 10 · 11 · 12 szorzat?
(A) 1 (B) 2 (C) 3 (D) 4

b) Melyik az a legnagyobb szám az alábbiak közül, amivel a 7428 osztható?
(A) 4 (B) 6 (C) 12 (D) 24

c) Hány százaléka az 50-nek a 75?
(A) 66%-a (B) 125%-a (C) 75%-a (D) 150%-a

d) Hány hegyesszöge lehet legfeljebb egy konvex négyszögnek?
(A) 1 (B) 2 (C) 3 (D) 4

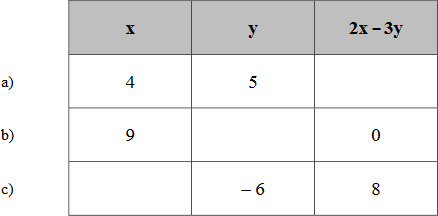
8. Írd be a táblázatba a hiányzó számokat!
Írd le a számolás menetét is!

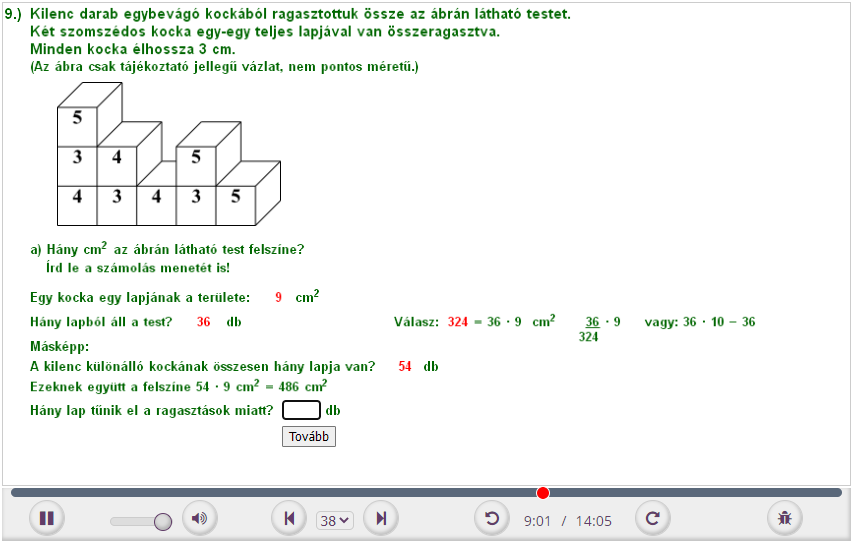
9. Kilenc darab egybevágó kockából ragasztottuk össze az ábrán látható testet.
Két szomszédos kocka egy-egy teljes lapjával van összeragasztva.
Minden kocka élhossza 3 cm.
(Az ábra csak tájékoztató jellegű vázlat, nem pontos méretű.)

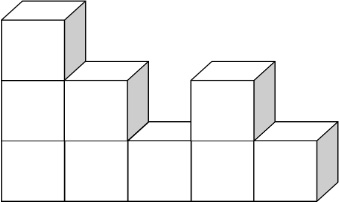
a) Hány cm 2 az ábrán látható test felszíne?
Írd le a számolás menetét is!

10. A városi labdarúgóklub toborzót rendezett, amelyre előzetesen kellett jelentkezni. Az előzetesen jelentkezők része nem jelent meg a toborzón. A megjelentek része teljesítette a fizikai felmérés követelményeit, a többiektől elbúcsúztak az edzők.
A fizikai elmérést eredményesen teljesítőknek labdás gyakorlatokat kellett végezniük, amelyeket 40%-uk teljesített hibátlanul, őket leigazolta a klub.
A városi labdarúgóklubnak 28 új igazolt játékosa lett.

a) Hányan jelentkeztek előzetesen a toborzóra?
Írd le a számolás menetét is!

Hihetetlenül gyorsan tudsz készülni matekból a felvételire az egyedi módszereknek és a jól felépített tananyagnak köszönhetően:

6. osztály: milyen feladatok voltak?

Nem túlzás azt mondani, hogy a hatodikosok számára készített felvételi a legnehezebb a 3 közül. 45 perc jut 10 feladatra, amik nagyon nehezek a tanulók számára. Minden évben van olyan feladat, aminek megoldásához egyenlet kell, amit sok diák még nem tanult megoldani. Ezen kívül bonyolult algebrai kifejezésekkel is meg kell küzdeni. Nézzük típusok szerint mi várta a felvételizőket!

1. feladat: Műveletek elvégzése (átlagos 1. feladat. Fókuszban van a műveleti sorrend alkalmazása)
2. feladat: Táblázat adataira vonatkozó kérdések (ez a típus is jellemző a hatodikos felvételire)
3. feladat: Mértékegységátváltás (ugyanazok a mennyiségek szinte minden évben)
4. feladat: Nehéz szöveges feladat (2021-ben és 2020-ban könnyebb volt, 2019-ben hasonló)
5. feladat: Nehéz igaz-hamis (időigényes feladat)
6. feladat: Összeszámlálás (a feladat nehézsége, hogy nem tudja a diák, hogy hány megoldás van)
7. feladat: Térlátás (gondolkodtató feladat)
8. feladat: Közepes nehézségű szöveges feladat (egyenletmegoldás)
9. feladat: Közepesen nehéz szöveges kerületszámítással
10. feladat: Szöveges feladat (hosszú, de összességében nem nehéz)

Nézzük részletesen a feladatokat, megoldásokkal együtt!

Csináld velünk a 2022-es matematika felvételi első 6 feladatát interaktív megoldásokkal, amikből rengeteget tanulhatsz:

Megtetszettek az interaktív tananyagok? Rengeteg videót találsz még az oldalunkon, ami segít felkészülni, és elérni a céljaid!

Készen állsz még négy feladatra? Csatlakozz hozzánk, és oldd meg velünk a 2022-es matematika felvételi 7-10. feladatát!

Az interaktív megoldásokhoz be kell jelentkezned! Ha még nincs fiókod, akkor regisztrálj!

Ezek voltak a feladatok:

1. Végezd el a kijelölt műveleteket!

a) 15 − (5 − 3) =

b) 168,2 − 8,2 : 2 =

c) ((−3) − 7) − (−17) =

d) 6 ∙ 2,5 : 3 =

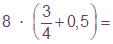
e)

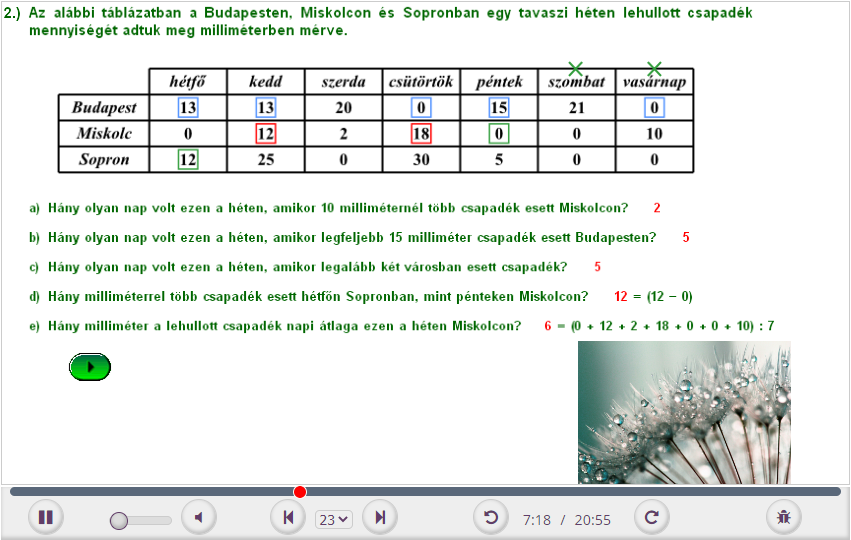
2.) Az alábbi táblázatban a Budapesten, Miskolcon és Sopronban egy tavaszi héten lehullott csapadék mennyiségét adtuk meg milliméterben mérve.

a) Hány olyan nap volt ezen a héten, amikor 10 milliméternél több csapadék esett Miskolcon?

b) Hány olyan nap volt ezen a héten, amikor legfeljebb 15 milliméter csapadék esett Budapesten?

c) Hány olyan nap volt ezen a héten, amikor legalább két városban esett csapadék?

d) Hány milliméterrel több csapadék esett hétfőn Sopronban, mint pénteken Miskolcon?

e) Hány milliméter a lehullott csapadék napi átlaga ezen a héten Miskolcon?

3. Pótold a hiányzó mérőszámokat!

a) 1,23 m = __________ cm

b) 1,2 liter + 3 dl = __________ dl

c) 0,5 kg + 75 dkg + __________ g = 150 dkg

d) 75 perc = __________ óra

e) 1 m 2 − __________ dm 2 = 2 dm 2

4. Gombóc Artúr fogyókúrába kezdett. A fogyókúra 2. napjától kezdődően minden nap feleannyi csokit evett meg, mint az azt megelőző napon úgy, hogy a 4. nap végére még 1000 gramm csokoládéja megmaradt. A harmadik nap végén 1500 gramm csokija volt.

a) Hány gramm csokit evett meg a 4. napon?

b) Hány gramm csokija lesz az 5. nap végére?

c) Hány gramm csokit evett meg az 1. napon?

d) Hány gramm csokija volt a fogyókúra kezdetén?

5. Az ábrán egy négyzetrács kilenc rácspontja látható. A négyzetrács egy rácsnégyzetének oldala 1 cm hosszú. A kilenc pont közül kiválasztunk három pontot, amelyek egy háromszög három csúcsát alkotják. Az alábbi eseményekről döntsd el, hogy biztos vagy lehetséges, de nem biztos vagy lehetetlen! Írj X-et a táblázat megfelelő oszlopába!

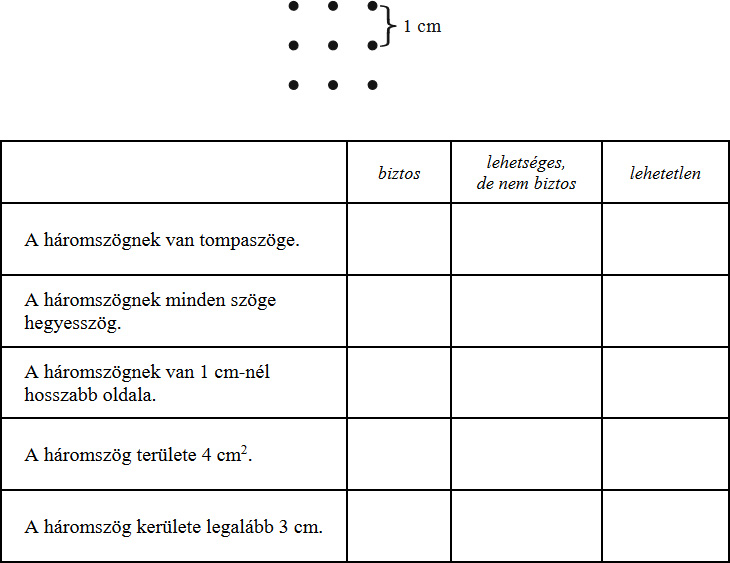
6. Sorold fel az összes olyan páratlan négyjegyű természetes számot, amelynek minden számjegye kisebb 3-nál és van legalább három egyforma számjegye!

7. Egy kocka lapjait a következőképpen számoztuk meg. Az egyik lapjára felírtuk az 1-es, majd az ezzel szemközti lapjára a 3-as számot. Ezután a kocka többi lapjára 2-es számot írtunk.

a) Hány olyan lap van a kockán, amelyre a 2-es számot írtuk?

b) Mennyi a kocka lapjaira írt számok összege?

c) Hány olyan 2-essel számozott lap van a kockán, amellyel szemben lévő lapon is 2-es szám van?

d) Hány olyan éle van a kockának, amely egy páros és egy páratlan számot tartalmazó lapot határol?

e) A kocka minden csúcsába beírtuk az abban a csúcsban találkozó lapokra írt számok összegét. Mennyi a kocka csúcsaiba írt számok összege?

8. Bálintéknak három kutyájuk van: Morzsi, Panír és Zsömi. Bálint megmérte a három kutya tömegét. Megállapította, hogy Zsömi 25 kg-mal nehezebb Morzsinál, és Zsömi 17 kg-mal nehezebb Panírnál. A három kutya tömege együtt 54 kg.

a) Mi a neve a legnagyobb tömegű kutyának?

b) Hány kilogrammal nehezebb Panír Morzsinál?

c) Hány kilogramm a kutyák tömege?
Morzsi: _____ kg
Panír: _____ kg
Zsömi: _____ kg

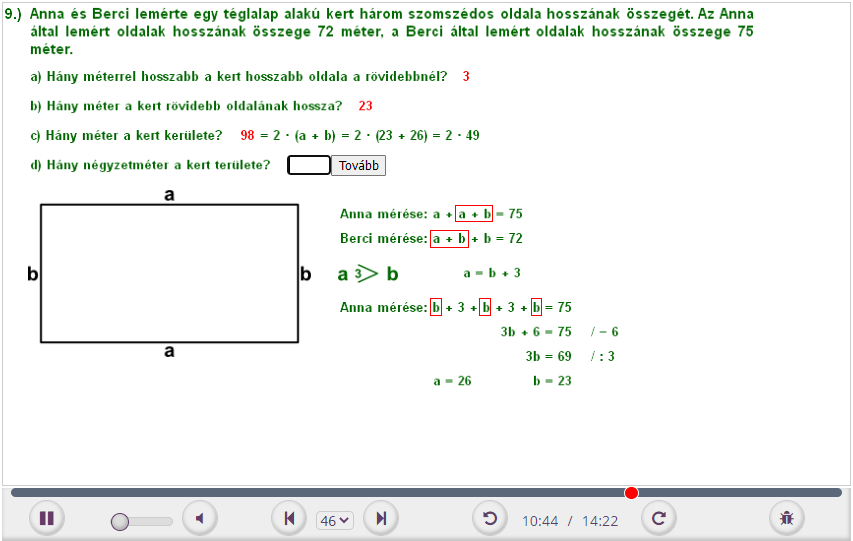
9. Anna és Berci lemérte egy téglalap alakú kert három szomszédos oldala hosszának összegét. Az Anna által lemért oldalak hosszának összege 72 méter, a Berci által lemért oldalak hosszának összege 75 méter.

a) Hány méterrel hosszabb a kert hosszabb oldala a rövidebbnél?

b) Hány méter a kert rövidebb oldalának hossza?

c) Hány méter a kert kerülete?

d) Hány négyzetméter a kert területe?

10. Egy fagyizóban a vásárlók tölcsérbe vagy kehelybe kérhetik a fagylaltot. A fagylaltjukat kérhetik csokiöntettel vagy anélkül. Egy nyári vasárnapon 213-an kérték kehelybe a fagylaltjukat. Tölcsérbe 362-vel többen kérték a fagylaltot, mint kehelybe. Ezen a napon a tölcsérbe kért fagylaltjukra 540-en nem kértek csokiöntetet, a kehelybe kért fagylaltjukra 85-en nem kértek csokiöntetet. (Egy vásárló egyféle fagylaltot kért.)

a) Hányan kérték a fagylaltjukat tölcsérbe?

b) Hányan kértek csokiöntetet a kehelybe kért fagylaltjukra?

c) Összesen hányan kértek csokiöntetet a fagylaltjukra?

d) Hányan vásároltak fagylaltot ezen a vasárnapon?

Megtetszettek az interaktív videók? Képzeld minden felvételihez szükséges témakörhöz készítettünk tananyagot. Fejlődj velünk gyorsan, és írj sikeres felvételit!

4. osztály: milyen feladatok voltak?

A negyedik osztályos felvételizőknek sincsen könnyebb dolguk, mint hatodikos és nyolcadikos társaiknak. Nagyon fiatalon, sokan talán először kerülnek versenyhelyzetbe matematikából. Fontos rutint szerezni a fiataloknak mire eljutnak a felvételi megírásáig. A feladatok hasonlóak voltak 2022-ben is, mint az előző években. Mutatjuk, hogy épült fel ebben az évben a negyedikes központi matematika felvételi!

1. feladat: Feladatok számokkal (számkártyák, kerekítés, helyiérték – nehézség a több megoldás)
2. feladat: Hányféle színezés lehetséges? – (minden évben nehézség, hogy nem tudja a vizsgázó hány megoldás van)
3. feladat: Mértékegységváltás (műveletekkel fűszerezve)
4. feladat: Diagram elemzés
5. feladat: Nehéz térgeometria feladat (szinte minden évben előfordul hasonló)
6. feladat: Logikai feladat (következtetéssel, esetkizárással)
7. feladat: Hányféle kitöltés lehetséges? (számolásokkal)
8. feladat: Szöveges + lehetőségek kiválasztása (jó sok számolásssal)
9. feladat: Négyzet kerülete (+ 2 könnyű kérdés)
10. feladat: Sorozatos feladat (sok számolással)

Nézzük részletesen a feladatokat, megoldásokkal együtt!

Készítettünk egy színes interaktív videót, amiben meg tudod velünk oldani a 2022-es matematika felvételi első 6 feladatát. Ezekből nagyon sokat tudsz tanulni, és rutint szerezhetsz a feladatmegoldásban:

Tanulj velünk interaktívan! Mi kérdezünk, te válaszolsz. Talán te is meglepődsz majd, hogy milyen gyorsan fejlődsz!

Nincs más hátra, nézzük meg a maradék négy feladatot! Tarts velünk, oldjuk meg együtt a 2022-es matematika felvételi 7-10. feladatát!

Az interaktív megoldásokhoz be kell jelentkezned! Ha még nincs fiókod, akkor regisztrálj!

Ezek voltak a feladatok:

1. Oldd meg a következő feladatokat!

a) Melyik az a szám, amely kerek százas, nagyobb, mint 700, de kisebb, mint 1000?
Írd le az összes megoldást! Vigyázz, a rossz válaszért pontlevonás jár!

b) Panni perselyében 7 db 50 Ft-os és 4 db 20 Ft-os van.
Mennyi pénz van összesen a perselyben?

c) Karikázd be azokat a kártyákat, amelyeknek az eredménye nem 750!

d) Alkoss olyan háromjegyű számokat az számkártyákból, amelyeknek százasokra kerekített értéke 200! Vigyázz, a rossz válaszért pontlevonás jár!

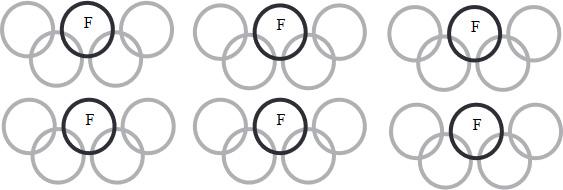
2. Számkirály saját olimpiai kitűzőt tervez. Hányféleképpen színezheti ki az 5 karikát, ha ezt tudja róluk:

• az olimpiai 5 karika fekete (F), sárga (S), piros (P), zöld (Z) és kék (K) színekből áll;
• a felső sorban a fekete van középen;
• a sárga nem érintkezik a pirossal;
• a sárga egy sorban van a zölddel?

Írd be a lehetséges eseteket az ábrába! Használd a színek kezdőbetűjét!
Vigyázz, több ábra van, mint lehetőség! A hibás megoldásért pontlevonás jár.

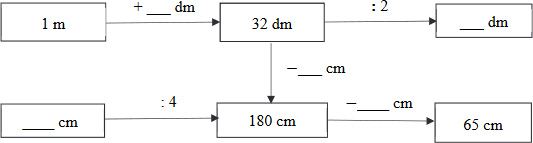
3. Írd be a műveleteknek megfelelő mérőszámokat az ábrába! Figyeld a nyilak irányát!

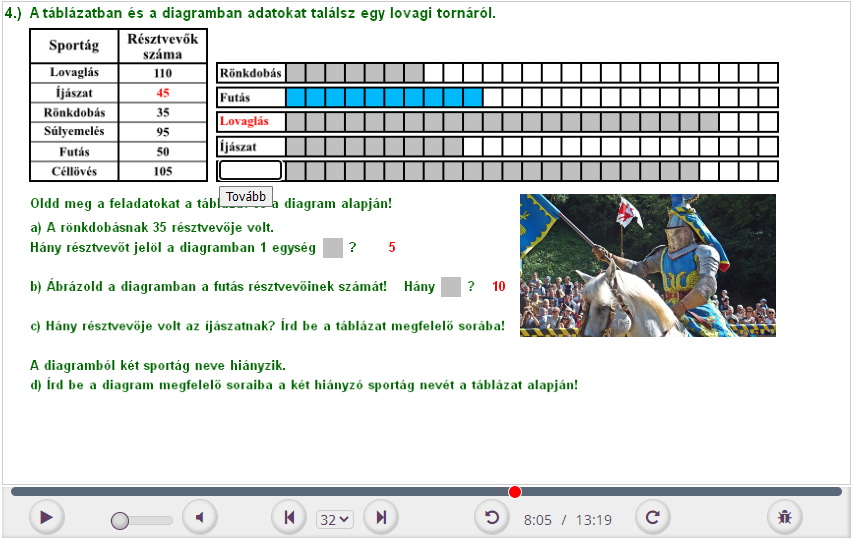
4. A táblázatban és a diagramban adatokat találsz egy lovagi tornáról.

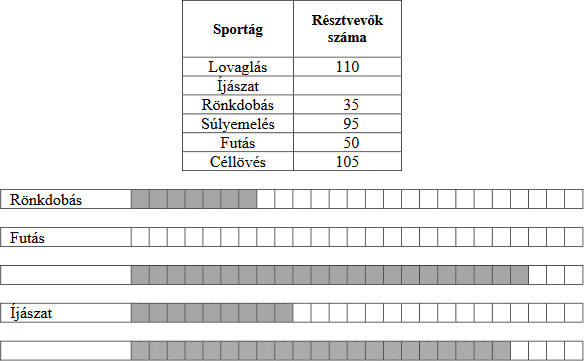
Oldd meg a feladatokat a táblázat és a diagram alapján!

a) A rönkdobásnak 35 résztvevője volt.
Hány résztvevőt jelöl a diagramban 1 egység ?

b) Ábrázold a diagramban a futás résztvevőinek számát!

c) Hány résztvevője volt az íjászatnak? Írd be a táblázat megfelelő sorába!

A diagramból két sportág neve hiányzik.

d) Írd be a diagram megfelelő soraiba a két hiányzó sportág nevét a táblázat alapján!

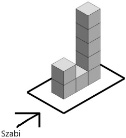
5. Szabi 1 cm élű kiskockákból egy J betűt épített.
A szomszédos kockákat összeragasztotta.
Ezután Szabi leült az asztalhoz.
A nyíl mutatja, honnan nézi az építményt.

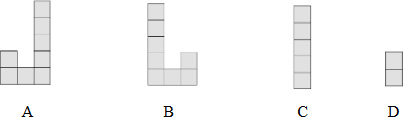
a) Melyik ábrát látja Szabi az alábbiak közül? Karikázd be a megoldás betűjelét!

Szabi a J betűt belemártotta egy vödör sárga festékbe úgy, hogy nem látszott ki egy darabja sem.

b) Hány olyan kiskocka alkotja a J betűt, amelynek 5 lapja lett sárga?
Összesen hány lapja lett sárga a J betűt alkotó kiskockáknak?

c) Szabi 8 ugyanilyen kiskockából egy nagyobb kockát épített. Hány centiméter hosszú a nagyobb kocka egy éle?

6. Gergőről, Marciról és Ádámról a következőket tudjuk:

• Gergő a legidősebb.
• Marci barna hajú.
• A szőke hajú fiút nem Ádámnak hívják.
• Nem a fekete hajú fiú a legfiatalabb.

Az állítások alapján töltsd ki a táblázatot!

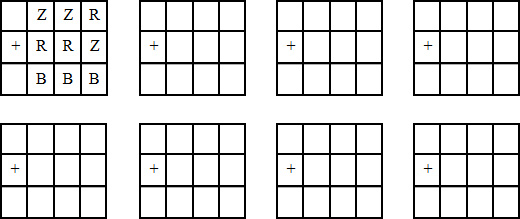
7. Egy betűkkel megadott összeadásban az azonos betűk azonos számjegyeket jelölnek.
Az alábbi betűk csak a következő számok lehetnek:

Z = 1, 2, 3, 4 ; R = 1, 2, 3 ; B =3, 5

Add meg az összes lehetőséget úgy, hogy a műveletek eredménye helyes legyen!
Vigyázz, több hely van, mint lehetőség! A hibás megoldásért pontlevonás jár.

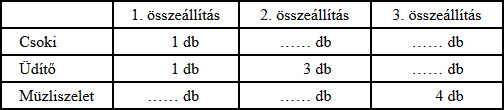
8. Panni 900 tallérral megy a büfébe, ahol 3-féle áru közül válogathat:

1 csoki: 210 tallér
1 üdítő: 130 tallér
1 müzliszelet: 100 tallér

a) Legfeljebb hány darab árut vehet Panni?
b) Hány tallérja marad, ha mindenből egy darabot vásárol?
c) Hány tallért fizetett, ha 3 csokit és 1 üdítőt vásárol?
d) Ha mind a háromféle áruból vesz legalább egy darabot és összesen 7 darab árut vásárol, akkor ezt milyen összeállításban teheti meg? Írd be a hiányzó adatokat a táblázatba!

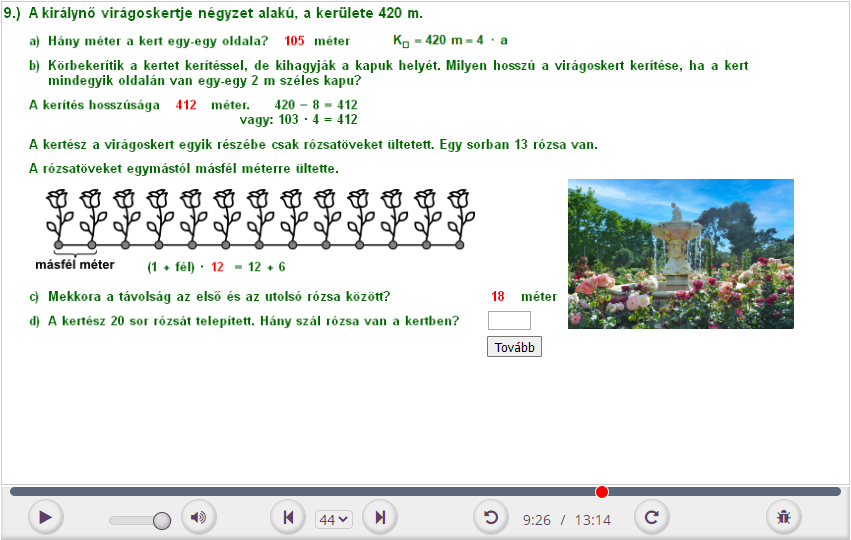
9. A királynő virágoskertje négyzet alakú, a kerülete 420 m.

a) Hány méter a kert egy-egy oldala
b) Körbekerítik a kertet kerítéssel, de kihagyják a kapuk helyét. Milyen hosszú a virágoskert kerítése, ha a kert mindegyik oldalán van egy-egy 2 m széles kapu?

A kertész a virágoskert egyik részébe csak rózsatöveket ültetett. Egy sorban 13 rózsa van.
A rózsatöveket egymástól másfél méterre ültette.

c) Mekkora a távolság az első és az utolsó rózsa között?
d) A kertész 20 sor rózsát telepített. Hány szál rózsa van a kertben?

10. Panni egy 320 oldalas könyvet olvas.

Az első napon 9 oldalt olvasott. Folyamatosan, minden nap három oldallal többet olvas, mint amennyit az előző napon elolvasott.

a) Hány oldalt olvasott el összesen az első három nap alatt?
b) Hány oldalt olvas a 8. napon?
c) Hányadik napon olvas pontosan 36 oldalt?
d) A 13. napon, vasárnap olvasta ki a könyvet. A hétnek melyik napján kezdte el az olvasást?

Készítettünk egy egész tréninget, amivel felkészülhetsz egy sikeres felvételire! A tréning különleges felépítésének köszönhetően gyorsan tudsz fejlődni a felvételi feladatok megoldásában. Nézz bele ezekbe a tananyagokba is!

Így segíthetsz gyermekednek matekból (rádió riport)

Hogyan segíthetjük gyermekeinket, hogy minél gördülékenyebben vegyék az új tanévben az új matekos akadályokat?