C feladatgyűjtemény

Kedves 10. osztályos diákok! Szakaszvizsgára gyakorló feladatok 10. évfolyam Közeleg a szakaszvizsga időpontja, amelyre 019. április 1-én kerül sor. A könnyebb felkészülés érdekében adjuk közre ezt a feladatsort,

Egységes Érettségi Feladatgyűjtemény Matematika Megoldások Letöltése, Egységes Érettségi Feladatgyűjtemény. Matematika, Megoldások I.

A feladatok megoldásához atlasz nem használható. Page 2. 2. Page 3. 3. Page 4. 4. Page 5. 5. Page 6. 6. Page 7. Page 8. 8. Mérnöki Fizika Feladatgyűjtemény – BME ELoSZo. A Mérnöki Fizíka c. tantárgy oktatása a BME Közlekedésmérnöki Karán az. I978-ban életbe lépett kari tanterv bevezetésével kezdődött meg. Az 199I-. Fizikai feladatgyűjtemény – KMKSZ R 58 Fizikai feladatgyűjtemény a középiskolák 9–11. osztálya számára. 4., bővített kiadás. – K. — U. : Oszvita Tankönyvkiadó, 1992. – 224 old. illusztr. Mérnöki Fizika Feladatgyűjtemény Feladatgyűjtemény – Pécsi Tudományegyetem önmegbecsülés, mely a feladatok teljesítéséből, illetve a kompetencia. A csoportot foglalkoztató időszerű problémák összegyűjtése, mely orientálja a nevelőt a. feladatgyűjtemény kerékpáros fókusszal Térkép, repülős-, katonai-, erdész-, tájfutós-, turista-, autós-, kerékpáros térkép, a lakóhely tér- képe, térképvázlat. Célok: bemelegítés, ráhangolódás. SZERVES KÉMIAI FELADATGYŰJTEMÉNY Jelen szerves kémiai feladatgyűjtemény II.

Egységes matematika feladatgyűjtemény megoldások pdf – Pdf dokumentumok és e-könyvek ingyenes letöltés

(nik E N; k sn). n! (n kỳ. Teljes indukcióval bizonyítsuk be, hogy a következő állítások igazak, ha az n pozitív egész szám nagyobb. FELADATGYŰJTEMÉNY Konfárné Nagy Klára. Kovács István. Trembeczki Csaba. Urbán János. Mozaik Kiadó – Szeged, 2010. FELADATGYŰJTEMÉNY sokszínű. MEGOLDÁSOK. feladatgyűjtemény – MatHelp FELADATGYŰJTEMÉNY sokszínű. MEGOLDÁSOK. oldali ábrán láthatók. b) A B C = (sárga körcikk a jobb oldali ábrán);. Számelméleti feladatgyűjtemény 2015. márc. 2. Az számelméleti feladatok és megoldási módszereik nagyon sokfélék, változatosak. Az egyszerű feladatok szinte játékos módon megoldhatók. Statisztika feladatgyűjtemény I. 1. ALAPFOGALMAK; VISZONYSZÁMOK; GRAFIKUS ÁBRÁZOLÁS 9. Fogalmak. 7. A GYAKORLÓ FELADATOK MEGOLDÁSA 287. 1. Feladatgyűjtemény – easyMaths Egy vékony, körív alakú szigetelő fonal λ homogén lineáris töltéssűrűséggel. R sugarú tömör fémhenger felületén egyenletes σ felületi töltéssűrűség van. Topográfiai feladatgyűjtemény Topográfiai feladatgyűjtemény.

A bosszú csapdájában 2 évad 57 rész magyarul videa 2 resz magyarul videa teljes

Egységes érettségi feladatgyűjtemény. Matematika, Megoldások I.

éves gyógyszerészhallgatók részére készült, a főkollégiumi. szerkezete zárja, tekintettel arra, hogy a szerves kémia a gyógyszerészi kémia alapozó. ELNEVEZÉSE ÉS SZERKEZETI KÉPLETE. C. Feladatgyűjtemény tevékenység- és termelésmenedzsment. termelésmenedzsment témaköréhez kapcsolódó számítási feladatokat fokozatosan elsajátíthatóvá tenni. segítik az eligazodást a feladatok megoldása és a levezetések értelmezése során. Raktározási költség: 200 Ft/tonna. VI. 20. 120. robotika feladatgyűjtemény – H-Didakt A feladatgyűjtemény alapvetően a MINDSTORMS robotok programozását helyezi a. figyelő blokkokat (sárga színűek és a Sensor csoportban találhatók). Feladatgyűjtemény – Hidrodinamikai Rendszerek Tanszék 2019. máj. 28. szivattyú járókeréknek a dimenziótlan elméleti ψ(φ) jelleggörbe egyenletét. a) A sebesség, majd abból a térfogatáram számítása: s m. Egy vizet szállító szivattyú H=40m, Q=20m3/h munkapontban dolgozik egy keringető.

OOP-előkészítő C feladatok

A dinamikus tömböt és a hosszat mindenhol együtt kezeld! C-s sztringkezelő függvényeket ( strcpy , strlen ) használni lehet.

3 . Sztringből kiszedi a megadott karaktereket

Egészítsd ki az előző programot egy olyan függvénnyel, amelyik egy megadott sztringből kiszedi a paraméterként kapott karakter összes előfordulását! A dinamikus tömb a szűrés után is pont akkora legyen, amekkora kell!

4 . Memóriakezeléses elvi hibás verem

Alább egy C-ben megírt verem adatszerkezet. A verem_init() függvény inicializálja az addig memóriaszemetet tartalmazó struktúrát. A verem_berak() függvény betesz egy számot a verembe. Ha kell, átméretezi a dinamikus memóriaterületet. A verem_free() egy feleslegessé vált verem dinamikus területét szabadítja fel.

A program memóriakezelési hibát tartalmaz. Hol? Hogyan lehet javítani?

A fenti kódban az elvi hiba a v1=v2 értékadásnál van. Itt ugyanis minden egyes adattag átmásolódik v1 -be v2 -ből; ez a darabnál például nem lenne gond, a pointernél viszont nagyon is az. Ugyanis innentől kezdve v1 és v2 pointere ugyanoda mutat, és a vermek nem működnek majd helyesen. Például az egyik verembe berakott adat a másikban is lehet, hogy meg fog jelenni. A v1.adat pointer ilyen módon történő felülírása memóriaszivárgást is okoz.

A struktúrák közötti értékadás maga egyébként működik, lefordul, már a sima C is ismeri! Nem az a hiba, hogy ilyen nincs, hanem amit csinál, az nem jó nekünk itt. (Gyakorlatilag a struktúra értékadásával megsértjük azt a szabályt, hogy nem nyúlunk a struktúra belsejébe – ugyanis kívülről nem tudhatjuk, hogy le szabad-e egyesével másolni az adattagjait. Ezt csak az tudja, aki a struktúrát kezelő függvényeket megírja.) Írni egy másolós függvényt, amelyik egyesével átmásolja a struktúra adattagjait, az ugyanúgy rossz, mintha egy sima értékadással lerendezzük, mert akkor a memóriaszivárgás és a rossz pointerek ugyanúgy meglesznek. Ezen kívül, az egymásra mutató pointerek mindenképpen rosszak, nem csak akkor, ha a két verem darabszáma vagy kapacitása épp eltérő.

A memória felszabadítása lesz az, ahol a program lefagy; egészen pontosan v2 felszabadítása. v1.adat és v2.adat ugyanoda mutat, ezért a felszabadító függvény kétszer próbálja meg majd azt a memóriaterületet felszabadítani ( free() vagy delete[] , attól függ, hogyan vannak megírva).

Javítani úgy lehet, ha az értékadás helyett másoló függvényt írunk, és a v1=v2 értékadást egy verem_masol(&v1, &v2); sorra cseréljük.

5 . Melyik változó hova kerül?

Rajzold le az alábbi program változóinak elhelyezkedését a memóriában, amikor a végrehajtás a *-gal jelölt résznél tart! Melyik változó hova kerül (globális, verem, dinamikus memóriaterületre)? Az egyes pointereket nyíllal jelöld, hova mutatnak. Van egy hiba a programban. Hol? Hogyan lehet javítani?

A program változói a lenti ábrán láthatóak. Az s globális területre kerül, mivel függvényen kívül van. Az m a verembe, mivel az a main() függvény globális változója. Ezeken kívül pedig a heapre kerül a két malloc() -olt tömb.

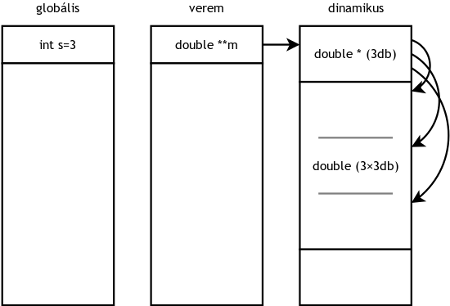
Az első foglalt tömb pointereket tartalmaz, mégpedig hármat. Ennek a tömbnek az első elemébe egy pointert teszünk, amelyet a malloc() függvény ad; ez kilenc darab double változónak hely. A többi pointert úgy inicializáljuk, hogy ennek a tömbnek a belsejébe mutat, 3 és 6 elemmel arrébb.

A kódban a hiba az, hogy a main() függvényben csak az első, pointereket tartalmazó tömb kerül felszabadításra. A második, double elemeket tartalmazó nem. (Egy malloc → egy free!) Javítani legegyszerűbben úgy lehet, hogy a free(m) sor elé egy free(m[0]) hívást írunk.

KOMPETENCIA ALAPÚ FELADATGYÛJTEMÉNY MATEMATIKÁBÓL 8. ÉVFOLYAM MEGOLDÁSOK

1 KOMPETENCIA ALAPÚ FELADATGYÛJTEMÉNY MATEMATIKÁBÓL 8. ÉVFOLYAM MEGOLDÁSOK Algebra és számelmélet 1. a) 0, 45; b)0, 5, 5, 40, 50, 55; c) 0, 1, 4, 5, 7, 0,, 5, 9, 40, 4, 45, 48, 50, 51, 54, 55, 57; d),, 6, 8, 9, 1, 4, 7, 8, 41, 4, 44, 46, 47, 49, 5, 5, 56, 58, 59.. a) ; b) < 10; 8; 6; 4; ; 0; 1; ; ; 4; 5; 6; 7; 8; 9>; c) ; d)< 9; 7; 5; ; 1>.. A B = , A B = , A \ B = , B \ A = . 4. Mind a két szakkörbe 5-en járnak. 5. Legalább egy táborban 1 tanuló volt. Csak egy táborban 14 tanuló volt. Mindkét táborban 7-en voltak. 8 S 7 B 6 6. A B = , A B = , A \ B = , B \ A = . A tengelyesen és középpontosan szimmetrikus négyszögek sorszámai. 7., 8. 1

2 7. A = < 1; ; ; 4; 5; 6>, A \ B = < 1; ; 5>, (A B ) = , B = < 6; 4; ; 0; ; 4; 6; 8>, B = < 5; ; 1; 1; ; 5; 7; 9>. ALGEBRA ÉS SZÁMELMÉLET 8. Legalább egy szakkörre 8-an járnak. Az informatika szakkörre -en, a sportjátékok szakkörre 5-en jelentkeztek. 50 S I

3 Számok és mûveletek 1. a) 6 89; b) 6 416; c) 6 89; d) (4 + ) = = 18 4 (4 + ) = = (4 + ) + 4 = 0 4 ( 4) = = 0 (4 4) + = 1. a) ; b),; c) 5 ; d) a,5 0,7 8,9 4, ,4 b 1,9,01 1,01 0,0 0, c 44,65 1,467 8, ,7 Szabály: a b = c, c : a = b, c : b = a. 5. a) 175 4; b) 715,89498; ; d) = 44 c) 84 = = = = 47 ( ) 7 = 6 7 = 19 ( + ) 7 = = 6 7 = a) ; b) 0 75 ; c) ; d) : 17 = 460, 1,975 : = 0,059, 5,64 : 87 = 0, a) 59; b) : 1 = 890; c) d) 1. 0 ;

4 10. (18 54) : = 4 18 (54 : ) = 4 18 : 54 = 4 SZÁMOK ÉS MÛVELETEK 54 : 18 : = 1 (54 : ) 18 = 4 54 (18 : ) = a) 1; b) ; c) ; d) 1; e) 81; f) b) c) d) e) a) f) a) 1 1 ; b) ; c) ; d) , 9, 5, 1, 16 84, 768, a) 5 7 ; b) 9 ; c) 4 9 ; d) 6 5 ; e) a 1 ; f) y x + z + t. 16. a) 5 ; b) 5 ; c) 8 ; d) 6 ; e) ; f) x. 17. a) ; b) 1 ; c) a) ; b) ; c) 65; d) a) >; b) >; c) =; d) =; e) =; f) > a) 1 ; b) ; 19 c) ; a) 4 096; b) ; c) ; d) 1968 ; 187 e ) ; f ) a) 8, 6,, 4; b) 9, 7, 1, 7; c) 4, 6, 5, 6; d) 8, 6, 4,. 79 d) ; 4 e) 045,. 4

5 SZÁMOK ÉS MÛVELETEK Osztó, többszörös, oszthatóság. a b K Annak a téglalapnak a legkisebb a kerülete, amelynek oldalai egyenlõek.. 4 = 4. A 4-nek 15 osztója van: 1. 4, 6, 9, 1, 18, 4, 7, 6, 81, 108, 16, A = , B = . A B Közös osztók: 1. 6, 9, 18; (6;54) = A két szám: 10 és = = 1, 60 = 5 7, = (16; 646) = 16, [16; 646] = vel -mal 4-gyel 5-tel 6-tal 10-zel 5-tel 697 I I I N I N N I I N I I I I 541 N I N N N N N 000 I N I I N I I 0. -vel -mal 6-tal 4-gyel 1-vel 15-tel 4-gyel 9 7 igen lehet lehet igen lehet nem lehet 64 lehet lehet lehet lehet lehet lehet lehet 4 1 nem lehet nem nem nem nem nem 0 igen lehet lehet lehet lehet lehet lehet 5

6 SZÁMOK ÉS MÛVELETEK 1. a) 4; b) 18; c) 10; d) 10.. A:, 5, 8; B: 0,, 6. A + B =, A + B = 8, A + B = 14.. Az ismeretlen osztó: 6. ( ) : 6 = 70 : 6 = a) Az összeg osztható, mert páros és számjegyeinek összege osztható kilenccel. b) Az összeg osztható, mert páros és számjegyeinek összege osztható hárommal. c) Az összeg osztható, mert osztható néggyel és a számjegyeinek összege osztható kilenccel. 5. a) = 9 1 = 1 = ; b) : 048 = 18 : 11 = 7 = 18; c) = 5 8 = 1 = ; d) : = 1 : 10 = = 9; e) = 6 9 = 15 = ; f) : = 6 7 : 6 5 = 6 = 6; g) = = 0 = 4 15 = ; h) : 8 19 = 0 : 1 = 7 = < 18 14, 5000 >5 000, < a) 5; b) -1; c) 8; d) -7; e) 1; f) 9. Számok normálalakja 8. a), ; b) 4,8 10 ; c), ; d) 4,0 10 ; e) ; f), 10; g) 4, ; h), ; i), ; j), ; k) 1, 10 1 ; l) a) 1 000; b) 0,000 5; c) 5 410; d) 0, ; e) ; f) 0, ; g) ; h) 0, K = 56 dm, T = dm. 41. a = 16 dm, T = 56 dm. 4. a = 8 dm, k = dm. Számok négyzete, négyzetgyöke 6

8 SZÁMOK ÉS MÛVELETEK 49. a) 54 = 916 = 9,16 10 ; b) 14 = = 1, ; c) 0 = = 9, ; d) = = 1, ; e) = = 76, ; f) = = 49, ; g) 0,6 = 0,969 = 9,69 10 ; h) 0,04 = 0, = 5, ; i) 0,00 6 = 0, = 1, ; j) 0, = 0, = 9, ; k) 0, = 0, = 60, ; l) 0, = 0, = 8, , 69 = 1, 64, 1, 4 =, 66, 45, 56 = 6, 75, 8, 7 = 9, 15, 1 = 1, 5 =, 4, 10 =, 16, 7 =, 65, 8 =, 8, 18 = 4, 4,, 5 = 4, 74, 0 = 5, 48. 1, 988 = 1, 41, 19, 88 = 4, 46,, 5 = 1, 8,, 5 = 5, = 4, 4, 180 = 1, 4, = 4, 4, = 14, 1, 8 = 1, 4, 0, 18 = 0, 44, 0, 018 = 0, 14, 0, 0018 = 0, = 1, 7, 1 40 = 6, 6, = 70,, =, 0, 7 = 0, 87, 0, 046 = 0, 14, 0, = 0, 068, 0, = 0, K = 1 dm, T = 10,565 dm. 55. K = 191, cm, T = 84,84 dm. 56. a = 44,5 m, T = 1980,5 m. 57. a = 1,8 dm, K = 7, dm. 58. a = 74,9 m, K = 99,6 m. 59. a = 0,005 km, K = 0,08 km. 8

9 Pitagorasz-tétel 1. a) c = 1 cm; b) y = 1 cm; c) m = 1 cm; d) c = 5,6 dm; e) y = 1,9 m; f) m = 8,57 cm.. A derékszögû háromszög átfogója 1, cm hosszú.. A derékszögû háromszög átfogója 65 dm hosszú, K = 157 dm, T = 1058 dm. 4. A derékszögû háromszög hiányzó befogója 8,1 m hosszú, K =,41 m, T = 19,11 m. 5. A négyzet átlója 16,97 cm hosszú, K = 48 cm, T = 144 cm. 6. A négyzet átlója 4,4 cm hosszú, a = cm, T = 9 cm. 7. Az egyenlõ szárú háromszög K = 4, cm, T = 7,9 cm. 8. Az egyenlõ szárú háromszög K = 6 cm, T = 8,6 cm. 9. Az egyenlõ szárú háromszög K = 46, dm, T = 46,9 dm. 10. Az egyenlõ szárú háromszög K = 6 cm, T = 60 cm. 11. A szabályos háromszög K = 54 cm, T = 140,1 cm. 1. A téglalap hiányzó oldala 15, cm hosszú, K = 56,4 cm, T = 197, cm. 1. A téglalap köré írható kör sugara 5,045 dm. 14. K = 4,4 cm, T = 70 cm. 15. K = 100 mm, T = 6, mm. 16. K = dm, T = 5,8 dm. 17. K = 80 cm, T = 10 cm. 18. K = cm, T = 44 cm. 19. A húr hossza 11, cm. 0. h 1 =,6 cm, h = 17 cm. 9

10 PITAGORASZ-TÉTEL 1. e. AO = 5, BO = 5,9, CO = 1,9.. AB = 5,8, CD = 6,7. 4. K = 6, A lapátló 11, cm, a testátló 1,86 cm. 6. A kocka felszíne 178 cm. 7. A téglatest testátlója 17 cm hosszú. 8. A leghosszabb lapátló 14,4 cm, a leghosszabb és a legrövidebb lapátló közötti különbség 4,97 cm, a téglatest testátlója 15,6 cm hosszú. 9. a) 0 cm; b),5 cm; c) 6,4 cm; d) 5,76 cm. b) < d) < c) < a) 0. Szögei szerint Pitagorasz tételének a megfordítása derékszög tompaszög derékszög hegyesszög derékszög hegyesszög tompaszög Kerület 1 cm cm 0 m 5 cm 0 dm 5 mm 7,6 dm Terület 6 cm cm 0 m 104 cm 7,5 dm 54 mm,6 dm 10

11 Algebrai kifejezések 1. a) b = a 6; b) a + b = ; c) 5a + b; d) (a b) ; e) (a + b) c; f) a 0,7 b; g) x y ; h) (x y) 5 x y ; i) c d ; j) c : 7 6; k) 1, ab ; ab ; x y ; 1,0 xyz; 1ab; xy. 6. Együttható,7 4, Változó c b x c x e x f xy 4. a-val egynemû: 0,9a, 8a; 5. ab -tel egynemû: 7ab ; 7ab 1,ab-vel egynemû: ab,, 4, ab, ba; 9 a b-vel egynemû: 7a b, 1a b. 7ab ab ; ; ab ab; 5ba; a; a b. 6. ab 5ab ; ab a b b ; ab; 5 ba a. 7. a) b) c) d) y, 7y, y, 6y, 11y ; 4 15 x, x, 8x, 17x, x ; xy, xy, xy, 1xy, xy; ab, ab,, ab, 9ab, ab. 17 ab 1 7 xy 8. 7ab, a b. ab, a,, x y. ab ab 5xy 4 11

12 ALGEBRAI KIFEJEZÉSEK ab, ab a a b, 5, ab, ab, xy ab, a,, 4x y. 5xy a ) 1+ y; b ) x; c ) x + xy+ y ; d ) y x + 5x y + y. a ) ab+ ab; b ) x y xy; c ) 8x + ; d ) x + x y. a ) y 1; b ) 7x + 17y z; c ) 4, 5xy 5xz 19, yz; d ) 0, 85y + z + 0 a ) 6, 45; b ) 0; c) 0; d) a ) 5; b ) ; c ) ; d ) a ) 10; b ) ; c ) 1; d ) a ) 17; b ) ; c ) 0; d ) a ) 6a ; b ) 4a ; c ) 6x y; d ) x y. 6 5x y 4x 6x y 8x y 105x 4 y x.,5x y 4,x 4 6,x y,8x 4 y 10,5x 5 y 5 4 xy x y x y 5 xy 5x 4 y a ) a ; b ) a; c ) 4x ; d ) 0, 4yz. y 0,6x 10x x 06, y x y y x y 4x y xy 15x 40x 4 y y x 4x y 1

13 ALGEBRAI KIFEJEZÉSEK 1. a ) a ; b ) x ; c ) x ; d ) y ; e ) a ; f ) a b ; g ) a b ; h ) ab Szorzat összeggé alakítása 4. a) 6x 10x ; b) 1x 8x ; c) 1y 8y ; d) 18x 1x. 5. a) 1x 8x ; b) 1x 5 8x 4 + 4x ; c) 6x 9x + 1x; d) 6x 7x a ) 5x 19y; b ) 4x+ 10; c ) 7y 4xy+ 8y 6x; d ) 4c 6cd 8c d. 4 ab b 4,5a b 15ab 4 4 0,6a 0,6a 0,6a b a b 1 4 ab 1 5 ab 0,75a b a ) 6xya; b ) 9x 6x; c ) xy y+ x 6; d ) x x. 5 5 a ) 8( a b); b ) 5ab( 1 ab); c ) 4x ( x x + 1); d ) xy ( 1+ y 5x + xy). a ) ( ); b ) ( 6 ); c ) 7( b a + a+ b a ab+ b x xy+ y ); d ) z( 9x + 6xy+ y ). a ) 7a( 7a b+ ab ); b ) xy( 9x+ 6+ y); c ) 4( 16x 8x+ 1); d ) 17ab( ab + b). a ) E = ; b ) F = a; c ) G = xy ; d ) H = xz. a ) x+ y, alaphalmaz: és x y; b ) x y, alaphalmaz: és x y; c) x+ y, alaphalmaz: és x y; d ) x y, alaphalmaz: és x y. a a( a+ 9b). a ) x 7; b ) ; c ) ; d ). b ( a+ b) 4 9 ab 1 ab a b 5 ab 1 a 15 5 b 5 ab a 1

14 1. a) x = ; b) x = ; c) x = 1. Egyenletek, egyenlõtlenségek. a) x = 0; b) y = 0; c) azonosság; d) azonosság.. a) x = 1; b) x = 1; c) y = a) a = 9; b) b = 5; c) c = a) a = 4; b) b = ; c) x = a) a 1 = 0, a = 7; b) b 1 =, b = 5; c) c 1 = 0, c =, c = a) a1 =, a =, a = ; b) 1 b1 =, b =, b =. 8. > x. 9. x x x. 1. a ) 6 x; b ) x. 1. Azonosságok: a), c), f), g), h). 14. a) 4; b) x ; c) ; d) 4, a) a = ; b) a = 9; c) a =

15 Egyenlettel megoldható Szöveges feladatok 1. Jutkának 810 Ft-ja, Mártának 1040 Ft-ja van.. Az egyik polcon 56 befõtt, a másik polcon 74 befõtt van.. Az egyik szám 5, a másik szám Lolának 1640 Ft-ja, Balázsnak 10 Ft-ja volt eredetileg. 5. Az elsõ polcon 108, a második polcon 6, a harmadik polcon 7 könyv van. 6. Egy menü 840 Ft-ba került. 7. α = 45, β = 60, γ = α = 84, β = 60, γ = A ketrecben eredetileg 7 nyúl volt. 10. A matematikadolgozat átlaga,48 volt. 11. Laci 10 éves, édesanyja 8 éves, édesapja 40 éves. 1. Panni 9 éves, apukája 9 éves. 1. Az egyik szám 95, a másik szám A teremben 14 háromlábú és 178 négylábú szék van. 15. A parkolóban 7 motor és 15 autó van. 16. a) 11, 5 < x; b) x 64. 1, 5 15

16 17. x 10. EGYENLETTEL MEGOLDHATÓ a (cm) x 7 6 b (cm) x c (cm) x 10 9 K (cm) 9 Számok helyi értékével kapcsolatos feladatok 18. Ez a kétjegyû szám az Ezek a kétjegyû számok a 1, 4, 5, 46, 57, 68, Az eredeti kétjegyû szám a Az eredeti kétjegyû szám a 6.. Az eredeti kétjegyû szám a 8.. Az eredeti kétjegyû szám a Az eredeti kétjegyû szám a Az eredeti kétjegyû szám a Az eredeti kétjegyû szám a Az eredeti kétjegyû szám a Ez a háromjegyû szám a A betonozási munkák 4 napig tartanak Ede és Máté együtt 5 órát dolgozott Ede 8 órát dolgozott összesen. 4. Gábor összesen 7,5 napot dolgozott.. Gábor összesen 7 napot dolgozott. 9 Munkavégzéssel kapcsolatos feladatok 16

17 4. Még munkást kell beállítani. EGYENLETTEL MEGOLDHATÓ Mozgásos feladatok 5. A motor Pécstõl 8,5 km távolságra éri utol a teherautót, 5,5 óra múlva. 6. A város a falutól 6 km távolságra van. 7. Szegedtõl a kiskert 6 km távolságra van. 8. A személygépkocsi és a teherautó 9 óra 5 perckor találkozott Kistelektõl 7 km távolságra. 9. A személygépkocsi 1 óra 57 perckor Szegedtõl 57,6 km távolságra éri utol a teherautót. 40. Lolka Bolkát 70 másodperc alatt körözi le. 41. Bence és Gergõ 150 másodperc múlva találkoznak. Keveréses feladatok 4. A 80%-os oldatból 5,45 grammra van szükség. 4. A 5%-os oldatból,5 kg-ra, a 45%-os oldatból 1,75 kg-ra van szükség. 44. A 10%-os ecetsavból 0 grammra, a 0%-os ecetsavból 90 grammra van szükség. 45. A 80%-os oldatból 0 grammra, a 50%-os oldatból 50 grammra van szükség. 46. A keverék elkészítésével 56 százalékos oldatot kapunk. 47. A szükséges töménység eléréséhez 600 gramm vizet öntsünk a sóoldathoz. 48. A keverék hõmérséklete 50 C lesz. 49. A közös hõmérséklet 60 C lesz. 50. A 90 C-os vízbõl 4,15 kilogrammra van szükség. 51. A 0 C-osból 8 kilogramm, a 80 C-osból 0 kilogramm víz szükséges. 17

18 Geometriai ismétlés Alapfogalmak, alapszerkesztések

19 GEOMETRIAI ISMÉTLÉS. a) b) c) d) 19

20 GEOMETRIAI ISMÉTLÉS 4. Ha az egyenes érinti a körvonalat, akkor ilyen pont van. Ha az egyenes és körvonal távolsága cm-nél kisebb, akkor p 4 ilyen pont van. Ha az egyenes és körvonal távolsága cm, akkor 1 ilyen pont van. Ha az egyenes és körvonal távolsága cm-nél nagyobb, akkor 0 ilyen pont van. 5. A sík azon pontjai, amelyek e-tõl cm-nél nem nagyobb és P-tõl 1 cm-nél nem kisebb távolságra vannak Két megoldás esetén a pont és egyenes távolsága: d(p, e) < 6 cm. Egy megoldás esetén a pont és egyenes távolsága: 6 cm. Nincs megoldása a feladatnak, ha a pont és egyenes távolsága: d >6 cm. 0

21 GEOMETRIAI ISMÉTLÉS 8. Ha a feladatnak nincs megoldása, akkor a három pont egy egyenesen van

22 GEOMETRIAI ISMÉTLÉS 1. Szerkeszd meg az adott szögeket! Mekkora a megszerkesztett szög mellékszöge? α =15 β =10 γ =157,5 δ =150 ϕ =45 μ =105 λ =15 ω = a) b) α = β α = γ c) d) α + δ = 180 α + ϕ = 180

23 GEOMETRIAI ISMÉTLÉS a) lehet; b) biztos, 1; c) lehet, 1; d) biztos. 16. nem; páros; és tengelyesen is; a tengelyek metszéspontja. 17. a) b)

25 4. Egyenlõ szakaszok: AF = FB, CE = EF, BE = EA, BC = BF. Egyenlõ szögek: CEB = 60, BEF = 60, FEA = 60, EAF = 0, β = ϕ = Vázlat: GEOMETRIAI ISMÉTLÉS A két magasságvonal által bezárt szög: δ = Szerkesztés: 5

26 8. a) T = 0 cm ; b) K = 0 cm; c) m a = 1 cm, m b = 5 cm, d)s a = 1,6 cm, s b = 7,81 cm; e) r = cm. GEOMETRIAI ISMÉTLÉS m c = cm; 9. Négyszögek 0. H, I, I, H, I, I, H, H, I, H, I. 1. Rombusz: β = 18, γ = 4, δ = 18 ; paralelogramma: α = 74, β = 106, γ = 74, δ = 106 ; trapéz: α = 44, β = 55, γ = 15 ; deltoid: α = 110, γ = 0, δ = α = 98, β = 89 ; α = 75, β = 11 ; α = 9,5, β = 9,5.. K = cm, T = 44 cm. 4. K = 66 cm, T = 5 cm. 5. K = 4 cm, T = 18 cm. 6. b = 5,66 cm, K = 5, cm, T = 8 cm. Szerkesztés menete: 1. 7 cm-es szakasz felvétele.. Egyik végpontjába 45 -os szög szerkesztése.. 7 cm-es oldallal 4 cm távolságra párhuzamos egyenes szerkesztése. 4. Ahol a 45 -os szög szára metszi a párhuzamost, onnan a 7 cm-es szakasz mérjük. 5. A kapott két végpont összekötése. 6

27 GEOMETRIAI ISMÉTLÉS 7. b = 8,54 cm, K = 7,08 cm, f = 1 cm, f** = 4 cm, T = 6 cm. Szerkesztés menete: 1. e átló felvétele.. a oldallal, mint szárral e alappal egyenlõszárú háromszög szerkesztése.. e felezõmerõlegesének megszerkesztése. 4. e felezõpontjából rámérem f*-ot. 5. A kapott pontot összekötöm e végpontjaival. Szerkesztés: 7

28 8. Egy csúcsból húzható átlók száma Az egy csúcsból húzott átlók ennyi háromszögre bontják a sokszöget GEOMETRIAI ISMÉTLÉS Sokszögek háromszög négyszög ötszög hatszög hétszög tízszög tizenhatszög n-szög n n Összes átlók száma ( n ) n Belsõ szögeinek összege (n ) 180 Külsõ szögeinek összege a) 65; b) 1980 ; c) a) 15; b) 880 ; c) a) A sokszög 6 oldalú. b) A sokszög 1 oldalú. c) A sokszög 4 oldalú. 4. a) A sokszög 7 oldalú. b) A sokszög 14 oldalú. c) A sokszög 0 oldalú. 4. a) A sokszög belsõ szögeinek összege 160. b) A sokszög belsõ szögeinek összege 060. c) A sokszög belsõ szögeinek összege a) A sokszög 8 oldalú. b) A sokszög 15 oldalú. c) A sokszög 17 oldalú. d) A sokszög 1 oldalú. 45. T 1 = 5 cm, T = 5 cm, T = 4 cm, T = 11 cm, a = 7,8 cm, b = 8,06 cm, K = 5,4 cm. 46. háromszög négyszög ötszög hatszög hétszög tízszög tizenhatszög n-szög 46. Középponti szögének nagysága Egy belsõ szögének nagysága Egy külsõ szögének nagysága Szimmetriatengelyeinek száma , ,5 6,5 60 n ( n ) 180 n 60 n n Középpontosan szimmetrikus-e? nem igen nem igen nem igen igen 8

29 47. a) 9; b) 140 ; c) 40 ; d) 9; e) nem. 48. a) 1; b) 150 ; c) 0 ; d) 1; e) igen. 49. a) A szabályos sokszög 18 oldalú. b) A szabályos sokszög 4 oldalú. c) A szabályos sokszög 6 oldalú. 50. a) A szabályos sokszög 18 oldalú b) A szabályos sokszög 5 oldalú. c) A szabályos sokszög 0 oldalú. GEOMETRIAI ISMÉTLÉS 51. K = 18 cm, m, 6 cm, T =, 9 cm, T =, 4 cm. a háromszög hatszög Szerkesztés: 5. a=, cm, K = 18, 4 cm, T =, 1855 cm, T = 5, háromszög nyolcszög 48 cm. Szerkesztés: 5. A kör 9

30 54. K = 7,68 cm, T = 11,04 cm. 55. A kerék átmérõje 0,64 m. 56. A körív hossza 75,6 cm, a körcikk kerülete 111,6 cm, a körcikk területe 60,88 cm. 57. A körív hossza 6,8 cm, a körcikk kerülete 5, cm, a körcikk területe 6,17 cm. 58. A pálya kerülete 57 m, a területe 696,5 m. 59. A keresett terület 40,19 cm A körszelet területe 41,04 dm. 6. A körszelet területe 45,5 cm. GEOMETRIAI ISMÉTLÉS R r d K T a) 7 cm cm 4 cm 6,8 cm 15,6 cm b) 9 cm 6 cm cm 94, cm 141, cm c) 10 cm 7 cm cm 106,76 cm 160,14 cm d) 8 cm 5 cm cm 81,64 cm 1,46 cm 6. A hulladék területe 4,05 cm, ez 1,5 százaléka a háromszög területének. 0

31 Térgeometria 1. A lapok száma 5, a csúcsok száma 6, az élek száma 9.. A hasábnak 9 lapja, 14 csúcsa és 1 éle van.. A hasábnak 1 lapja, 4 csúcsa és 6 éle van. 4. a) 7; b) 11; c) 10; d) a) 10; b) 8; c) 8; d) a) 0,7; b) 400; c) 56; d) m ; e) 80; f) mm ; g) 57; h) cm ; i) 8 000; j) dm. 7. a) 0,145; b) mm ; c),1 m ; d) cm ; e) 0,065; f) 0,46; g) 0, ; h) 1,; i) 750; j) 6,8. 8. A = 98 cm, V = 1080 (cm ). 9. A hasáb alapéle 4,5 dm, oldaléle 1,5 dm hosszú. A hasáb térfogata 7,75 dm. 10. A téglatest élei 1,8 dm,,7 dm, 4,5 dm hosszúak. Az edény térfogata 1,87 dm. Ebbe az edénybe 1,87 liter folyadék fér. 11. A hasáb felszíne 1 dm, térfogata 16 dm. 1. A hasáb felszíne 119,68 cm, térfogata 11cm. 1. A hasáb felszíne 148 cm, térfogata 10 cm. 14. Az edénybe 5,88 liter víz fér. 15. A tartály térfogata 156 dm, magassága 16 dm, a tartály felszíne 659,4 dm. 16. A henger felszíne 1507, dm, térfogata 617,8 dm. 17. A henger felszíne 1884 dm, térfogata 680 dm. 18. A két test felszínének aránya A 1 : A = 70,6 : 57,96, térfogatának aránya V 1 : V = 16 : A hulladék térfogata 1 85 cm, ez a rönk térfogatának 6, százaléka. 1

32 TÉRGEOMETRIA A gúla 0. A gúlának 8 lapja, 8 csúcsa és 14 éle van. 1. A gúlának 11 lapja, 11 csúcsa és 0 éle van.. A gúla éleinek a száma 5-nél nagyobb páros természetes szám lehet.. a) 10; b) 18; c) 9; d) a) 11; b) 15; c) 1; d) a) A gúla felszíne 96 cm, térfogata 48 cm. b) A gúla felszíne 1,96 dm, térfogata 1,78 dm. c) A gúla felszíne 84,56 cm, térfogata 1408 cm. 6. A gúla felszíne 110,4 cm. 7. A test felszíne 74 cm, térfogata 1 cm. 8. A test felszíne 194,88 cm, térfogata 188,16 cm. Az egyenes körkúp 9. a) A kúp felszíne 6,76 cm. b) A kúp felszíne 45,7184 dm. 0. a) A kúp felszíne 10,64 cm. b) A kúp térfogata 46 dm. 1. A kúp felszíne 565, cm, térfogata 401,9 cm.

33 . a) A = 1808,64 cm, V = 15,6 cm ; b) A = 105,76 cm, V = 411,5 cm.. A két kúp térfogatának aránya :. TÉRGEOMETRIA 4. A két kúp térfogatának aránya V 1 : V = 4 : A keletkezett test felszíne 149,464 cm, térfogata 18,5 cm. 6. A keletkezett test felszíne 8,6 mm, térfogata 14 mm. 7. A = 01,44 cm, V = 01,44 cm, a keletkezett hulladék térfogata 60,88 cm. 8. A keletkezett test felszíne ,5 cm, térfogata cm. 9. a) A test felszíne 44,9 cm, térfogata 9,0 cm. b) A test felszíne 0,8 cm, térfogata 9,7 cm.

34 Felvételire készülünk 1. x = 8, y = 10, z = 0,, w = 9.. 6,5, 19,5, 15, 1, 10, feladatsor. a) 0,0544; b) 500; c) 7; d) 0,44; e) a) Paliék 400 forintot fizettek. b) A eset = B eset. c) A esetben: 17,8 Ft, B esetben: 14 Ft. 5. a) Lekváros; b) db; c) 0%; d) 7 ; e) 167 db. 6. a) A boltba kötet érkezett. b) Az elsõ nap 576 kötetet adtak el. c) A második nap az eredeti készlet 4 százaléka fogyott el. 1 d) A negyedik napra a készlet része maradt meg a) 8-féle háromszög készíthetõ. b) 8-féle egyenlõ szárú háromszög készíthetõ. c) Az egyenlõ szárú háromszög készítésének nagyobb a valószínûsége. d) Annak, hogy a készített háromszög különbözõ oldalú, a valószínûsége a) Lehet, hogy igaz; b) lehetetlen; c) biztosan igaz; d) lehet, hogy igaz; e) biztosan igaz. 9. a) A háromszög oldalainak hossza a = 1 cm, b = 10 cm. b) Az alaphoz tartozó magasság 8 centiméter. c) A háromszög területe 48 cm. 10. V = 88 cm, A = 15 cm. 5 lapja piros:, 4 lapja piros:, lapja piros: 4, lapja piros:. 4

36 6. a) 1970 és 1980 között volt a legnagyobb változás. b) A lakóinak száma kb. 8%-kal csökkent. c) Átlagosan 107 lakója volt a településnek. 7. α = 0. FELVÉTELIRE KÉSZÜLÜNK 8. a) Az ötödik nap percig tornázott Ede. b) A napi maximális edzésidõ 40 perc. c) Az egy hónap során 105 percet, azaz 17,5 órát edzett. 9. a) Az üzlet 17,5 kg barackot kapott. b) Az elsõ nap 9,5 kg, a második nap 7 kg barack volt az eladott mennyiség. c) A barack eredeti ára 80 Ft/kg. d) A barack eladásából az üzlet bevétele 7 40 forint volt. 10. a) A kocka éle 14 centiméter. b) A kocka : A téglatest = 1176 : 60 = 94 : 565 c) A kisebb téglatest élei 6 cm, 14 cm hosszúak. A nagyobb téglatest élei 11 cm, 14 cm, 0 cm hosszúak. d) V kocka = 744 cm, V kisebb téglatest = cm. A két térfogat közötti eltérés cm. 6

37 Függvények, sorozatok Hozzárendelések 1. I) Nyíldiagrammal: II) Táblázattal: III) Szabállyal: x x IV) Grafikonnal: V) Egyenlettel: x = y. Az A elemei A K elemei Szabály: x x + 7

38 FÜGGVÉNYEK, SOROZATOK. A elemei (x) K elemei (y = x + ) A elemei (x) K elemei (y) Szabály: x x 5. a) Ez a hozzárendelés függvény, mert minden számhoz egy számot rendelünk. b) Ez a hozzárendelés függvény, mert minden sokszögnek egyetlen kerülete van. c) Ez a hozzárendelés nem függvény, mert lehet valakinek több testvére is. d) Ez a hozzárendelés nem függvény, mert egy számhoz több számot rendelünk. 8

39 e) Ez a hozzárendelés függvény, mert egy természetes számhoz egy természetes számot rendelünk. f) Ez a hozzárendelés függvény, mert egy ponthoz egyetlen pontot rendelünk. 6. Szabály: x x 1 FÜGGVÉNYEK, SOROZATOK 7. a) Z N, x x, y = x, g(x) = x ; b) Z Z, x x, y = x, f(x) = x; c) Z Z, x x +, y = x +, f(x) = x + ; d) Q Q, x x, y = x, f(x) = x; e) Q Q, x x, y = x, f(x) = x ; f) Q + 0 Q, x x, y = x, f(x) = x ; g) Z Z, x x, y = x, f(x) = x. 8. x g(x)

40 FÜGGVÉNYEK, SOROZATOK x f (x) x g(x) f( x)= x+ g(x) = x 1, y = x a) b) c) x 1 y =, ax ( ) = x; 1 1 y x, b( x) x; y< 1 1 x, c( x) < x. y 1 x y = 1 x y< 1 x 40

41 FÜGGVÉNYEK, SOROZATOK 5 1. a) y(x) < x + 5; b) yx ( )< x+ ; c) y(x) >x x f(x) x g(x) x h(x) x x x f(x) g(x) h(x)

42 FÜGGVÉNYEK, SOROZATOK 15. x x x f(x) g(x) h(x) A három grafikon egymással párhuzamos. Megegyeznek az együtthatóikban, különböznek a konstansokban m f =, m g =, m h = 4, m i = 6, m k = =, m l =. f(x) grafikonja a k(x) grafikonjával, g(x) grafikonja a l(x) grafikonjával a 1 (x) = 4x, a (x) = 4x + 5, a (x) = 4x +1, b 1 (x) = x, b (x) = x + 7, b (x) = x, c1 ( x)= x, c( x)= x, c( x)= x+. 4 4

43 FÜGGVÉNYEK, SOROZATOK 18. x f(x) 1 1 x g(x) 0 4 x h(x) A g(x) és h(x) függvények grafikonjai egymást metszik. A g(x) és f(x) függvények grafikonjai egymásra merõlegesek. A h(x) és g(x) függvények grafikonjai egymást metszik. 19. x x x f(x) g(x) h(x) A három grafikon az y tengelyt a 1 pontban metszi. A h(x) függvény grafikonja zár be nagyobb szöget az x tengellyel. A g(x) függvénynek nagyobb a meredeksége. 4

44 FÜGGVÉNYEK, SOROZATOK 0. P f (0; 4) Q f (1; 1), P g (0; 0) Q g (1; 4). 1.. Pe(;), 0 Qe 1;, Pf(; 0 -), Qf 1;

45 FÜGGVÉNYEK, SOROZATOK. 1 1 a ) ex ( ) = x ; b ) f( x) = x+ 1 ; c ) gx ( ) = x+ ; d ) hx ( ) =. 4. ax ( ) = x+ 5, bx ( ) = x, cx ( ) =, 1 dx ( ) = x, ex ( ) = x 5,, f( x) = 5 x +, 4 gx ( ) = x, hx ( ) = e(x) = x +, f(x) = x +, g(x) = x, h(x) = x, ix ( )= x 1. 45

46 FÜGGVÉNYEK, SOROZATOK 6. x f(x) g(x) h(x) A g(x)-et megkaphatjuk, ha az f(x)-et eltoljuk az y tengely mentén egységgel fölfelé. A h(x)-et megkaphatjuk, ha az f(x)-et eltoljuk az x tengely mentén 1 egységgel balra. g(x): a függvény értéket növelem -vel. h(x): a változót növelem 1-gyel. 7. x f(x) g(x) h(x) A g(x)-et megkaphatjuk, ha az f(x)-et eltoljuk az y tengely mentén egységgel lefelé. A h(x)-et megkaphatjuk, ha az f(x)-et eltoljuk az x tengely mentén egységgel jobbra. g(x): a függvény értéket csökkentem -vel. h(x): a változót csökkentem -vel. 8. x e(x) f(x) g(x) e(x) minimumhely: x = 0, minimumérték: y = 0, f(x) minimumhely: x =, minimumérték: y = 0, g(x) minimumhely: x =, minimumérték: y =. 46

47 FÜGGVÉNYEK, SOROZATOK 9. x f(x) g(x) h(x) Az f(x) grafikonjából a g(x) grafikonját megkaphatjuk, ha az f(x) grafikont eltoljuk az y tengely mentén 1 egységgel fölfelé. Az f(x) grafikonjából a h(x) grafikonját megkaphatjuk, ha az f(x) grafikont eltoljuk az x tengely mentén egységgel balra. 0. x a(x) b(x) c(x) a(x) grafikonjából b(x) grafikonját megkaphatjuk, ha a(x) grafikont eltoljuk az y tengely mentén egységgel lefelé. a(x) grafikonjából c(x) grafikonját megkaphatjuk, ha a(x)grafikont eltoljuk az x tengely mentén 1 egységgel jobbra. 1. x e(x) f(x) g(x) e(x)= x, f(x)= (x +), g(x)= (x + ). 47

48 FÜGGVÉNYEK, SOROZATOK e(x) minimumhely: x = 0, minimumérték: y = 0, f(x) minimumhely: x =, minimumérték: y = 0, g(x) minimumhely: x =, minimumérték: y =.. x e(x) f(x) g(x) h(x) e(x): minimumhely: x =, minimumérték: y = 0, f(x): maximumhely: x = 0, maximumérték: y = 1, g(x): maximumhely: x = 0, maximumérték: y =, h(x): maximumhely: x =, maximumérték: y = 0. 48

49 FÜGGVÉNYEK, SOROZATOK. Értelmezési tartomány: R. Értékkészlet: y [ 4; [; R. Minimumhely: x = 0. Minimumérték: y = 4. Menete: csökkenõ, x ] ; 0], növekvõ, x [0; [. Az f(x) függvény grafikonja az x = 4; 4 pontban metszi az x tengelyt. 4. Értelmezési tartomány: R. Értékkészlet: y. Minimumhely: x =. Minimumérték: y =. Menete: csökkenõ, ] ; ], növekvõ, [ ; [. Zérushely(ek): x = 5; Értelmezési tartomány: R. Értékkészlet: y 4. Minimumhely: x =. Minimumérték: y = 4. Menete: csökkenõ, ] ; ]. növekvõ, [; [. Zérushely(ek): x = 1; 5. 49

50 FÜGGVÉNYEK, SOROZATOK Egyenletek grafikus megoldása 6. x =, y = 1, M (;1) 7. Megoldások: M 1 ( 1; 0); M (; 8) f( x) = x+, g( x) = x. Megoldások: M 1 (0; ); M (6; 4). 50

51 9. Megoldások: M 1 ( ; 0); M (; 4). FÜGGVÉNYEK, SOROZATOK 40. A két kerékpáros 9 órakor találkozott, az A településtõl 0 kilométer távolságra. Szöveges feladatok megoldása grafikusan 41. Az elsõ órában 4 km-t tettek meg; pihentek, játszottak órát; hazaindultak 14 órakor; hazaértek 17 órakor; a túra km hosszú volt; összesen 9 órán át túráztak. 51

52 FÜGGVÉNYEK, SOROZATOK 4. A két társaság 10,6 órakor találkozott órakor indultak. A B jármû tartott pihenõt. A B jármûnek volt nagyobb az átlagsebessége. 10 óra 7,5 perckor találkoztak. Az A jármû 17,5 km, a B jármû 11,5 km utat tett meg a találkozásig. Az A-nak 4 óra; B-nek,5 óra volt az útja. 5

53 Sorozatok 1. a) 11, 14, 17. ; b). ; c) 11, 15, 0. ; d) 1, 15, 18. A kapott sorozat: 0, 1. 4, 5, 0, 1. a ) a = 1, a = 1, 1 a = 5, a 4 = 7; b ) b 1 =, b = 6, b = 11, b 4 = 18; c ) c 1 = 0, c = 1, c =, c 4 = 6; d ) d 1 = 4, d = 1, d = 1, d 4 = a) a n = a 1 + (n 1) 5; b) b n = b 1 ( ) n 1 ; c) c n = c 1 + (n 1) ; d) d n = d 1 + (n 1) ( ). Számtani sorozatok: a), c), d). 5. a 0 = 11, S 0 = Mindenkit le tudtak ültetni. Az utolsó sorba 4 szék került. 7. a 4 = 504, S 4 = a 0 = 1571,1, S 0 =

54 SOROZATOK 9. a a a a a a a a a = 8, = 7, = 6, = 5, = 4, =, =, = 1, = 0, a a = 6d, 9 0 6= 6d d = A keresett összeg a) 108,5 kg; b) 80 kg; c) 6 kg. Elemérnek ezek alapján a c) fogyókúrás receptet ajánlom. 1. Az 1. év végére Ft-ja, a. év végére Ft-ja, a. év végére Ft-ja, a 4. év végére Ft-ja lesz. Minden hányados azonos, 1,1 értékû. 1. Az elsõ év végén Ft volt az értéke. A második év végére Ft volt az értéke. Most Ft az értéke. Minden hányados azonos, 0,8 értékû a 7 = a 1 =, a = 6, a = 18, a 4 = 54, a 5 = 16, a 6 = 486. Összegük: Számtani sorozat lehet: c), f), e). Mértani sorozat lehet: a), d) a ). ; b) 5, 4, 8. ; c ) 1, 6. ; d ),, a) = ; b) = ; c) a 1 = 84; d) a 1 = 1. a 1 9 a 1 54

55 SOROZATOK 18. a = 9, illetve a = a) nem eleme; b) nem eleme. 0. Húsz év múlva a település lakóinak a száma 11 1 lesz. A település lakóinak a száma 4 év múlva lesz kevesebb nél. 55

56 Geometriai transzformáció, hasonlóság 1. H, I, I, I, H, I.. a) b). a) deltoid b) I, H, I, H, I, I. 4. a) b) A keletkezett síkidom deltoid. Szimmetriatengelye AC egyenese. A keletkezett síkidom egyenlõ szárú háromszög. Szimmetriatengelye AB egyenese. 56

57 GEOMETRIAI TRANSZFORMÁCIÓ, HASONLÓSÁG 5. Vázlat: 6. a) Ez a négyszög egyenlõ szárú trapéz. b) I, H, I, H, I, I. 7. Vázlat: Szerkesztés: Szerkesztés menete: 1. a alap felvétele.. a felezõmerõlegesének megszerkesztése.. m rámérése a felezõmerõlegesre. 4. A kapott pontban párhuzamost szerkesztek a-val. 5. A párhuzamos egyenesre rámérem a felezõmerõlegestõl jobbra és balra a c felét. 6. A kapott pontokat összekötöm a végpontjaival. 57

58 GEOMETRIAI TRANSZFORMÁCIÓ, HASONLÓSÁG 8. Három megoldás. Középpontos tükrözés 9. a) I; b) I; c) H; d) I A négyszög paralelogramma. Eltolás 1. Párhuzamosak: d, e, f; Egyenlõk: e; a ellentett vektora: d. Adott pont eltolása adott vektorral 1. egyenlõ, párhuzamos, egyenlõ, azonos, egybevágó 58

59 GEOMETRIAI TRANSZFORMÁCIÓ, HASONLÓSÁG Az eltolás vektora egyenlõ az A-ból A -be mutató irányított szakasszal. 59

60 GEOMETRIAI TRANSZFORMÁCIÓ, HASONLÓSÁG Hasonlósági transzformáció 19. a) I; b) H; c) I; d) I. Háromszögek hasonlósága 0. A B C λ a b c a b c = = a b c 4 4, ,75 10, ,5 1,5 10,5 1,5 60

61 GEOMETRIAI TRANSZFORMÁCIÓ, HASONLÓSÁG 1. Szakasz adott részekre osztása 4. 61

62 GEOMETRIAI TRANSZFORMÁCIÓ, HASONLÓSÁG 5. A középpontos hasonlóság transzformációja 6. a) b) 7. a) b) 6

63 GEOMETRIAI TRANSZFORMÁCIÓ, HASONLÓSÁG 8. a) b) 9. a) b) 6

64 GEOMETRIAI TRANSZFORMÁCIÓ, HASONLÓSÁG 0. a) b) 1. 64

65 GEOMETRIAI TRANSZFORMÁCIÓ, HASONLÓSÁG.. a) b) 4. 65

66 GEOMETRIAI TRANSZFORMÁCIÓ, HASONLÓSÁG 5. 66

67 Kombinatorika, valószínûség 1. A lehetséges sorrendek száma: JAD, JDA, ADJ, AJD, DAJ, DJA.. Péter 4 1 = 4-féle sorrendben készülhet fel a másnapi órákra.. Összesen 10 ötjegyû számot készíthetünk. a) 4; b) 48; c) 4; d) Összesen 600 hatjegyû számot készíthetünk. a) 96; b) 19; c)10; d)7. 5. A hat golyót 60-féleképpen állíthatjuk sorba héten keresztül tarthat a kártyacsata az adott feltételek mellett. 7. Az origóból A-ba 79-féle módon juthatunk el. 8. a) 5-féle módon; b) 1-féle módon; c) 5-féle módon; d) 18-féle módon. 9. A maratoni versenyen féle befutási sorrend lehetséges. 10. A megadott feltételnek 70 szám felel meg. Kiválasztási feladatok (a sorrend is számít) 11. A szigetnek legfeljebb lakosa lehet. 1. Az utakon különbözõ rendszámú autó futhat. 1. Az adott feltételnek 90 ötjegyû szám felel meg , 6 4, 6 5, Az elsõ három helyezés 6-féleképpen lehetséges. Kiválasztási feladatok (a sorrend nem számít) 16. Zsófinak 105-ször kell fagylaltot vennie a nyáron. 17. Az osztály tanulói közül a diáktanács tagjait 19-féle módon választhatták ki. 67

68 KOMBINATORIKA, VALÓSZÍNÛSÉG 18. Az a) esetben 495, a b) esetben 10-féle választási lehetõség van. 19. A buszjegyen 84-féle különbözõ lyukasztás lehetséges. 0. a) 150 módon; b) 100 módon; c) 15 módon; d) 65 módon lehetséges. 1. Tíz csoki vásárlása 1001-féleképpen lehetséges. 68

69 Valószínûség a) ; b) a) ; b) ; c) a ) ; b) ;. c) a ) ; 6 5 b) ; 6 1 c) a) ; b) ; c) A kiválasztott három szakaszból valószínûséggel szerkeszthetünk háromszöget a) ; b) ; c) 0; d) ; e) a) ; b) ; c) ; d) ; e) a) ; b) ; c) ; d) ; e) a) ; b) a) ; b) ; c) ; d) ; e) ; f)

70 VALÓSZÍNÛSÉG 1. Az öt piros golyóhoz 0 fehéret kell tenni, hogy a feltétel teljesüljön Annak a valószínûsége, hogy a légy a csempe fehér színû részére száll:. 4 Statisztika 14. a) b),7; c) ; d). 15. a) x = 8; b) x =. 16. a) 199; b) 1998; c) 16,9; d) 000 elõtt. 17. a) 148,4; b) 157,; c) 15,85; d) egyenlõ; e) a) 17; b) 19,; c) 17; d) 4; e) igen. 19. a) b) 5; c) ; d) 4,5. 70

71 Év végi tudáspróba 1. feladatsor 1. a) ; b); c) ; d).. a) 5,48; b) 1.. a) gx ( )= x 4; b) hx ( )= x x = Az alaphoz tartozó magassága 4 cm. A háromszög területe 168 cm. 6. a) 85; b) 5; c) A keverék hõmérséklete C lesz. A víz magassága 5 cm órakor találkoznak. A motorosnak még 79, km-t kell megtenni, hogy Dunaföldvárra érjen Együtt,6 óra alatt lesznek kész a) számtani; b) a 6 = 80; d = ; n = 69; c) 0; d)

72 1. a (b c) a b + c (a + b) c ÉV VÉGI TUDÁSPRÓBA = 4 7. feladatsor 18 7 a b = 4 7 1,4 1,4 74,65, = 9, 1 9 = a) X Y = ; b)y \ Z = ; c) Y X = ; d)(x Y) \ Z = = x 7

73 4. a) Menete: csökkenõ függvény. É. t.: R. É. k.: R. b) Menete: csökkenõ x [0; [; növekvõ x ] ; 0]. É. t.: R. É. k.: y. c) Menete: csökkenõ x ] ; ]; növekvõ x [; [. É. t.: R. É. k.: y 0. ÉV VÉGI TUDÁSPRÓBA 5. Az egyenlõ szárú háromszög területe 6 cm. 6. a) A 10%-os ecetbõl 4 liter %-os ecet készíthetõ. b) A 0%-os ecetbõl 9 liter %-os ecet készíthetõ. A 0%-os ecet vétele a gazdaságosabb, mert az abból készített %-os ecetbõl 1 liter 1 Ftba kerül. 7. Jenõ 9 éves és Benõ éves. 8. A két brigád együtt 5 napot dolgozott. 9. Pápától 144,5 km távolságra, 11 óra 40 perckor. 10. a) A szabályos sokszög 14 oldalú. b) Egy belsõ szöge 154, fokos. 7

74 ÉV VÉGI TUDÁSPRÓBA. feladatsor 1. a) 4 650,68; b) 4,696.. x.. Nóri most 4 éves. 4. Péter onnan tudta, hogy rossz a végösszeg, hogy a 545 nem osztható hárommal. 5. Milán a 9-es számra gondolt. 6. É. t.: R, É. k.: y 8. Menete: csökkenõ: x [1; [, növekvõ: x ] ; 1]. Szélsõérték: maximuma van, hely: x = 1, érték: y = Az számítógép eredeti ára Ft. 8. Az elsõ sorban 8 ülõhely van. A huszonegyedik sorban 108 ülõhely van. A nézõtéren 148 ülõhely van. 9. Még munkást kell beállítani, hogy kész legyenek 10 nap alatt a festéssel. 10. A belsõ tárolótér 18,4 dm. A bevonásra 87,6 dm anyag szükséges. 74

Gyakorló feladatok javítóvizsgára szakközépiskola matematika 9. évfolyam

Gyakorló feladatok javítóvizsgára szakközépiskola matematika 9. évfolyam Halmazok:. Adott két halmaz: A = kétjegyű pozitív, 4-gyel osztható számok B = 0-nél nagyobb, de 0-nál nem nagyobb pozitív egész

Hatvány, gyök, normálalak

Hatvány, gyök, normálalak 1. Számítsd ki a következő hatványok pontos értékét! 3 5 3 3 1 4 3 3 4 1 7 3 3 75 100 3 0,8 ( ) 6 3 1 3 5 3 1 3 0 999. 3. Számológép használata nélkül számítsd ki a következő

Egyenes mert nincs se kezdő se végpontja

Szakasz mert van két végpontja Egyenes mert nincs se kezdő se végpontja Tört vonal Szög mert van két szára és csúcsa Félegyenes mert van egy kezdőpontja 5 1 1 Két egyenes egymásra merőleges ha egymással

Add meg az összeadásban szereplő számok elnevezéseit!

1. 2. 3. 4. Add meg az összeadásban szereplő számok elnevezéseit! Add meg a kivonásban szereplő számok elnevezéseit! Add meg a szorzásban szereplő számok elnevezéseit! Add meg az osztásban szereplő számok

I. A gyökvonás. cd c) 6 d) 2 xx. 2 c) Szakaszvizsgára gyakorló feladatok 10. évfolyam. Kedves 10. osztályos diákok!

Kedves 10. osztályos diákok! Szakaszvizsgára gyakorló feladatok 10. évfolyam Közeleg a szakaszvizsga időpontja, amelyre 019. április 1-én kerül sor. A könnyebb felkészülés érdekében adjuk közre ezt a feladatsort,

Osztályozóvizsga-tematika 8. évfolyam Matematika

Osztályozóvizsga-tematika 8. évfolyam Matematika 1. félév 1. Gondolkozz és számolj! A természetes szám fogalma, műveleti tulajdonságok Helyiértékek rendszere a tízes számrendszerben: alakiérték, tényleges

Érettségi feladatok: Síkgeometria 1/6

Érettségi feladatok: Síkgeometria 1/6 2005. május 10. 4. Döntse el, hogy a következő állítások közül melyik igaz és melyik hamis! A: A háromszög köré írható kör középpontja mindig valamelyik súlyvonalra

Geometriai feladatok, 9. évfolyam

Geometriai feladatok, 9. évfolyam Szögek 1. Nevezzük meg az ábrán látható szögpárokat. Mekkora a nagyságuk, ha α =52 o fok? 2. Mekkora az a szög, amelyik a, az egyenesszög 1/3-ad része b, pótszögénél 32

ÍRÁSBELI BELSŐ VIZSGA MATEMATIKA 8. évfolyam reál tagozat Az írásbeli vizsga gyakorlati és elméleti feladatai a következő témakörökből származnak.

ÍRÁSBELI BELSŐ VIZSGA MATEMATIKA 8. évfolyam reál tagozat Az írásbeli vizsga gyakorlati és elméleti feladatai a következő témakörökből származnak. Időtartam: 60 perc 1. Halmazműveletek konkrét halmazokkal.

Lehet hogy igaz, de nem biztos. Biztosan igaz. Lehetetlen. A paralelogrammának van szimmetria-középpontja. b) A trapéznak két szimmetriatengelye van.

Geometria, sokszögek, szögek, -, 2004_01/5 Lili rajzolt néhány síkidomot: egy háromszöget, egy deltoidot, egy paralelogrammát és egy trapézt. A következő állítások ezekre vonatkoznak. Tegyél * jelet a

MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉP SZINT Síkgeometria

MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉP SZINT Síkgeometria 1) Döntse el, hogy a következő állítások közül melyik igaz és melyik hamis! a) A háromszög köré írható kör középpontja mindig valamelyik súlyvonalra

Racionális számok: Azok a számok, amelyek felírhatók két egész szám hányadosaként ( p q

Szóbeli tételek matematikából 1. tétel 1/a Számhalmazok definíciója, jele (természetes számok, egész számok, racionális számok, valós számok) Természetes számok: A pozitív egész számok és a 0. Jele: N

Matematika pótvizsga témakörök 9. V

Matematika pótvizsga témakörök 9. V 1. Halmazok, műveletek halmazokkal halmaz, halmaz eleme halmazok egyenlősége véges, végtelen halmaz halmazok jelölése, megadása természetes számok egész számok racionális

Matematika szóbeli érettségi témakörök 2016/2017-es tanév őszi vizsgaidőszak

Matematika szóbeli érettségi témakörök 2016/2017-es tanév őszi vizsgaidőszak Halmazok Halmazok egyenlősége Részhalmaz, valódi részhalmaz Üres halmaz Véges és végtelen halmaz Halmazműveletek (unió, metszet,

Az egyenes egyenlete: 2 pont. Az összevont alak: 1 pont. Melyik ábrán látható e függvény grafikonjának egy részlete?

1. Írja fel annak az egyenesnek az egyenletét, amely áthalad az (1; 3) ponton, és egyik normálvektora a (8; 1) vektor! Az egyenes egyenlete: 2. Végezze el a következő műveleteket, és vonja össze az egynemű

1. GONDOLKODÁSI MÓDSZEREK, HALMAZOK, KOMBINATORIKA, GRÁFOK

MATEMATIKA TÉMAKÖRÖK 11. évfolyam 1. GONDOLKODÁSI MÓDSZEREK, HALMAZOK, KOMBINATORIKA, GRÁFOK 1.1. HALMAZOK 1.1.1. Halmazok megadásának módjai 1.1.2. Halmazok egyenlősége, részhalmaz, üres halmaz, véges,

Geometria 1 összefoglalás o konvex szögek

Geometria 1 összefoglalás Alapfogalmak: a pont, az egyenes és a sík Axiómák: 1. Bármely 2 pontra illeszkedik egy és csak egy egyenes. 2. Három nem egy egyenesre eső pontra illeszkedik egy és csak egy sík.

8. feladatsor. Kisérettségi feladatsorok matematikából. 8. feladatsor. I. rész

Kisérettségi feladatsorok matematikából I. rész. Egy deltoid két szomszédos szöge 7 és 0. Mekkora lehet a hiányzó két szög? pont. Hozza egyszerűbb alakra a kifejezést, majd számolja ki az értékét, ha a=

Matematika osztályozó vizsga témakörei 9. évfolyam II. félév:

Matematika osztályozó vizsga témakörei 9. évfolyam II. félév: 7. Függvények: – függvények fogalma, megadása, ábrázolás koordináta- rendszerben – az elsőfokú függvény, lineáris függvény – a másodfokú függvény

Feladatok MATEMATIKÁBÓL II.

Feladatok MATEMATIKÁBÓL a 12. évfolyam számára II. 1. Alakítsuk át a következő kifejezéseket úgy, hogy teljes négyzetek jelenjenek meg: a) x 2 2x + b) x 2 6x + 10 c) x 2 + x + 1 d) x 2 12x + 11 e) 2x 2

Osztályozó- és javítóvizsga témakörei MATEMATIKA tantárgyból 2016 / tanév

9. évfolyam I. Halmazok Osztályozó- és javítóvizsga témakörei MATEMATIKA tantárgyból 2016 / 2017. tanév 1. Halmaz, részhalmaz fogalma, részhalmazok száma, jelölések 2. Intervallumok 3. Halmazműveletek

Osztályozó- és javítóvizsga. Matematika tantárgyból

Osztályozó- és javítóvizsga Matematika tantárgyból 2018-2019 A vizsga 60 perces írásbeli vizsga (feladatlap) a megadott témakörökből. A megjelölt százalék (50%) nem teljesítése esetén szóbeli vizsga is,

HASONLÓSÁGGAL KAPCSOLATOS FELADATOK. 5 cm 3 cm. 2,4 cm

HASONLÓSÁGGAL KAPCSOLATOS FELADATOK Egyszerű, hasonlósággal kapcsolatos feladatok 1. Határozd meg az x, y és z szakaszok hosszát! y cm cm z x 2, cm 2. Határozd meg az x, y, z és u szakaszok hosszát! x

Gyökvonás. Másodfokú egyenlet. 3. Az egyenlet megoldása nélkül határozd meg, hogy a következő egyenleteknek mennyi gyöke van!

1. Melyik a nagyobb? a) 6 5 vagy 5 7 b) vagy 11 10 vagy Gyökvonás 5 11 vagy 6 8 55 e) 7 vagy 60 16 1. Hozd egyszerűbb alakra a következő kifejezéseket! a) 7 18 b) 1 5 75 8 160 810 650 8a 5 a 7a e) 15a

NULLADIK MATEMATIKA ZÁRTHELYI

A NULLADIK MATEMATIKA ZÁRTHELYI 20-09-2 Terem: Munkaidő: 0 perc. A dolgozat megírásához íróeszközön kívül semmilyen segédeszköz nem használható! Csak és kizárólag tollal tölthető ki a feladatlap, a ceruzával

2. tétel Egész számok – Műveletek egész számokkal. feleletvázlat

1. tétel Természetes számok tízes számrendszer műveletek és tulajdonságaik Természetes számok, jele, jelölések, ábrázolása számegyenesen műveletek a természetes számok halmazán belül Tízes számrendszer

Fényi Gyula Jezsuita Gimnázium és Kollégium Miskolc, Fényi Gyula tér Tel.: (+36-46) , , , Fax: (+36-46)

Fényi Gyula Jezsuita Gimnázium és Kollégium 529 Miskolc, Fényi Gyula tér 2-12. Tel.: (+6-46) 560-458, 560-459, 560-58, Fax: (+6-46) 560-582 E-mail: fenyi@jezsuita.hu Honlap: www.jezsu.hu A JECSE Jesuit

Síkgeometria 12. évfolyam. Szögek, szögpárok és fajtáik

Szögek, szögpárok és fajtáik Szögfajták: Jelölés: Mindkét esetben: α + β = 180 Pótszögek: Olyan szögek, amelyeknek összege 90. Oldalak szerint csoportosítva A háromszögek Általános háromszög: Minden oldala

3 függvény. Számítsd ki az f 4 f 3 f 3 f 4. egyenlet valós megoldásait! 3 1, 3 és 5 3 1

Érettségi, M, I-es feladatsor, természettudomány.. Számítsd ki a C! összeget! log 4. Határozd meg a. Számítsd ki az egyenlet valós megoldásait! összeg értékét, ha és az 4. Adott az f : 0,, f. Adottak az

Feladatok MATEMATIKÁBÓL II.

Feladatok MATEMATIKÁBÓL a 12. évfolyam számára II. 1. Alakítsuk át a következő kifejezéseket úgy, hogy teljes négyzetek jelenjenek meg: a) x 2 2x + b) x 2 6x + 10 c) x 2 + x + 1 d) x 2 12x + 11 e) 2x 2

MATEMATIKA TANMENET SZAKKÖZÉPISKOLA 9.A, 9.D. OSZTÁLY HETI 4 ÓRA 37 HÉT ÖSSZ: 148 ÓRA

MINŐSÉGIRÁNYÍTÁSI ELJÁRÁS MELLÉKLET Tanmenetborító ME-III.1./1 2 Azonosító: Változatszám : Érvényesség kezdete: Oldal/összes: 1/6 Fájlnév: ME- III.1.1.Tanmenetborító SZK-DC-2013 2013. 09. 01. MATEMATIKA

Követelmény a 7. évfolyamon félévkor matematikából

Követelmény a 7. évfolyamon félévkor matematikából Gondolkodási és megismerési módszerek Elemek halmazba rendezése több szempont alapján. Halmazok ábrázolása. A nyelv logikai elemeinek helyes használata.

Osztályozóvizsga és javítóvizsga témakörei Matematika 9. évfolyam

Osztályozóvizsga és javítóvizsga témakörei Matematika 9. évfolyam 1. félév Gondolkozás, számolás – halmazok, műveletek halmazokkal, intervallumok – racionális számok, műveletek racionális számokkal, zárójel

Koordináta-geometria feladatok (középszint)

Koordináta-geometria feladatok (középszint) 1. (KSZÉV Minta (1) 2004.05/I/4) Adott az A(2; 5) és B(1; 3) pont. Adja meg az AB szakasz felezőpontjának koordinátáit! 2. (KSZÉV Minta (2) 2004.05/I/7) Egy

Az osztályozóvizsgák követelményrendszere 9. évfolyam

Az osztályozóvizsgák követelményrendszere 9. évfolyam Kombinatorika, halmazok Összeszámlálási feladatok Halmazok, halmazműveletek, halmazok elemszáma Logikai szita Számegyenesek intervallumok Algebra és

Pótvizsga matematika 7. osztály (Iskola honlapján is megtalálható!) Tételek

Pótvizsga matematika 7. osztály (Iskola honlapján is megtalálható!) Tételek 1. Hatványozás 2. Normálalak. Mértékegységek. Műveletek racionális számokkal (tört, tizedes tört) 5. Középpontos tükrözés 6.

Osztályozó és Javító vizsga témakörei matematikából 9. osztály

Osztályozó és Javító vizsga témakörei matematikából 9. osztály 1. félév 1. Kombinatorika, halmazok Számoljuk össze! Összeszámlálási feladatok Matematikai logika Halmazok Halmazműveletek Halmazok elemszáma,

Kisérettségi feladatgyűjtemény

Kisérettségi feladatgyűjtemény Halmazok 1. Egy fordítóiroda angol és német fordítást vállal. Az irodában 50 fordító dolgozik, akiknek 70%-a angol nyelven, 50%-a német nyelven fordít. Hány fordító dolgozik

Háromszögek, négyszögek, sokszögek 9. évfolyam

Háromszögek, négyszögek, sokszögek 9. évfolyam I. Pontok, egyenesek, síkok és ezek kölcsönös helyzetet 1) a pont, az egyenes, a sík és az illeszkedés alapfogalmak 2) két egyenes metsző, ha van közös pontjuk

1. Mit nevezünk egész számok-nak? Válaszd ki a következő számok közül az egész számokat: 3 ; 3,1 ; 1,2 ; -2 ; -0,7 ; 0 ; 1500

1. Mit nevezünk egész számok-nak? Válaszd ki a következő számok közül az egész számokat: 3 ; 3,1 ; 1,2 ; -2 ; -0,7 ; 0 ; 1500 2. Mit nevezünk ellentett számok-nak? Ábrázold számegyenesen a következő számokat

Matematika szóbeli érettségi témakörök 2017/2018-as tanév

Matematika szóbeli érettségi témakörök 2017/2018-as tanév 1. GONDOLKODÁSI MÓDSZEREK, HALMAZOK, LOGIKA, KOMBINATORIKA, GRÁFOK 1.1. HALMAZOK 1.1.1. Halmazok megadásának módjai 1.1.2. Halmazok egyenlősége,

Javítóvizsga témakörök, gyakorló feladatok 13. i osztály Témakörök

Javítóvizsga témakörök, gyakorló feladatok 13. i osztály Témakörök I. Gondolkodási módszerek, halmazok, logika, kombinatorika, gráfok Állítás (igazságérték), állítás tagadása, állítás megfordítása Halmazok

54. Mit nevezünk rombusznak? A rombusz olyan négyszög,

52. Sorold fel a deltoid tulajdonságait! 53. Hogy számoljuk ki a deltoid területét? A deltoid egyik átlója a deltoid Átlói. A szimmetriaátló a másik átlót és a deltoid szögét. A szimmetriatengely két ellentétes

EGYBEVÁGÓSÁGI TRANSZFORMÁCIÓK TENGELYES TÜKRÖZÉS

GEOMETRIA 1. Az A, B, C egy egyenes pontjai (ebben a sorrendben), AB szakasz 5 cm, BC szakasz 17 cm. F 1 az AB szakasz, F 2 a BC szakasz felezőpontja. Mekkora az F 1 F 2 szakasz? 2. Az AB és CD szakaszok

Függvény fogalma, jelölések 15

DOLGO[Z]ZATOK 9.. 1. Függvény fogalma, jelölések 1 1. Az alábbi hozzárendelések közül melyek függvények? a) A magyarországi megyékhez hozzárendeljük a székhelyüket. b) Az egész számokhoz hozzárendeljük

MATEMATIKA ÉRETTSÉGI május 10. KÖZÉP SZINT I.

1) Adott két pont: A ; 1 felezőpontjának koordinátáit! AB felezőpontja legyen F. MATEMATIKA ÉRETTSÉGI 005. május 10. KÖZÉP SZINT I. és B 1; Írja fel az AB szakasz 1 1 F ; F ;1 ) Az ábrán egy ; intervallumon

Elméleti kérdés minták (3 x 5 pont) 1. Definiálja két halmaz unióját! Készítsen hozzá Venn-diagramot!

Elméleti kérdés minták (3 x 5 pont) 1. Deiniálja két halmaz unióját! Készítsen hozzá Venn-diagramot!. Csoportosítsa a négyszögeket az oldalak párhuzamossága, és egyenlősége alapján! 3. Határozza meg a

MATEMATIKA TANMENET SZAKKÖZÉPISKOLA 12.E ÉS 13.A OSZTÁLY HETI 4 ÓRA 31 HÉT/ ÖSSZ 124 ÓRA

MINŐSÉGIRÁNYÍTÁSI ELJÁRÁS MELLÉKLET Tanmenetborító Azonosító: ME-III.1./1 Változatszám: 2 Érvényesség 2013. 09. 01. kezdete: Oldal/összes: 1/6 Fájlnév: ME- III.1.1.Tanmenetborító SZK- DC-2013 MATEMATIKA

Matematika 6. osztály Osztályozó vizsga

Matematika 6. osztály Osztályozó vizsga 1. Számok és műveletek 1. A tízes számrendszer Számok írása, olvasása, ábrázolása Az egymilliónál nagyobb természetes számok írása, olvasása. Számok tizedestört

1. Mit nevezünk egész számok-nak? Válaszd ki a következő számok közül az egész számokat: 3 ; 3,1 ; 1,2 ; -2 ; -0,7 ; 0 ; 1500

1. Mit nevezünk egész számok-nak? Válaszd ki a következő számok közül az egész számokat: 3 ; 3,1 ; 1,2 ; -2 ; -0,7 ; 0 ; 1500 2. Mit nevezünk ellentett számok-nak? Ábrázold számegyenesen a következő számokat

Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma) Megoldások

Megoldások 1. Határozd meg a szakasz hosszát, ha a végpontok koordinátái: A ( 1; ) és B (5; )! A szakasz hosszához számítsuk ki a két pont távolságát: d AB = AB = (5 ( 1)) + ( ) = 6 + 1 = 7 6,08.. Határozd

Osztályozóvizsga követelményei

Osztályozóvizsga követelményei Képzés típusa: Tantárgy: Nyolcosztályos gimnázium Matematika Évfolyam: 7 Emelt óraszámú csoport Emelt szintű csoport Vizsga típusa: Írásbeli Követelmények, témakörök: Gondolkodási

NULLADIK MATEMATIKA ZÁRTHELYI

NULLADIK MATEMATIKA ZÁRTHELYI 08-09-07 Terem: Munkaidő: 0 perc. A dolgozat megírásához íróeszközön kívül semmilyen segédeszköz nem használható! A feladatlap kizárólag kék vagy fekete tollal tölthető ki.

I. A négyzetgyökvonás

Definíció: Négyzetgyök a ( a : a a 0 I. A négyzetgyökvonás a ) jelenti azt a nem negatív számot, amelynek a négyzete a. a 0 b : b b R A négyzetgyök-függvény értéke is csak nem negatív lehet. Ha a b-t abszolút

Koordináta-geometria feladatok (emelt szint)

Koordináta-geometria feladatok (emelt szint) 1. (ESZÉV Minta (2) 2004.05/7) Egy ABC háromszögben CAB = 30, az ACB = 45. A háromszög két csúcsának koordinátái: A(2; 2) és C(4; 2). Határozza meg a harmadik

Matematika felső tagozat

Matematika felső tagozat 5. évfolyam Témakör 1. Gondolkodási módszerek 2. Számtan, algebra 3. Összefüggések, függvények, sorozatok 4. Geometria, mérés I. félév Követelmény A gondolkodási módszerek követelményei

SZAKKÖZÉPISKOLA ÉRETTSÉGI VIZSGRA FELKÉSZÍTŐ KK/12. ÉVFOLYAM

SZAKKÖZÉPISKOLA ÉRETTSÉGI VIZSGRA FELKÉSZÍTŐ KK/12. ÉVFOLYAM A vizsga szerkezete: A vizsga írásbeli és szóbeli vizsgarészből áll. 1.) Írásbeli vizsga Időtartama: 45 perc Elérhető pontszám: 65 pont Feladattípusok:

(d) a = 5; c b = 16 3 (e) b = 13; c b = 12 (f) c a = 2; c b = 5. Számítsuk ki minden esteben a háromszög kerületét és területét.

Euklidész tételei megoldások c = c a + c b a = c c a b = c c b m c = c a c b 1. Számítsuk ki az derékszögű ABC háromszög hiányzó oldalainak nagyságát, ha adottak: (a) c a = 1,8; c b =, (b) c = 10; c a

MATEMATIKA TANMENET SZAKKÖZÉPISKOLA 11B OSZTÁLY HETI 4 ÓRA 37 HÉT/ ÖSSZ 148 ÓRA

MINŐSÉGIRÁNYÍTÁSI ELJÁRÁS MELLÉKLET Tanmenetborító Azonosító: ME-III.1./1 Változatszám: 2 Érvényesség 2013. 09. 01. kezdete: Oldal/összes: 1/5 Fájlnév: ME- III.1.1.Tanmenetborító SZK- DC-2013 MATEMATIKA

3. a) 64; b) 32; c) 81; d) 1854; e) 8; f) 8; g) 1; h) 1; i) 1; j) 81 5 ; k) 1

KOMPETENCIA ALAPÚ FELADATGYÛJTEMÉNY MATEMATIKÁBÓL. ÉVFOLYAM MEGOLDÁSOK Számok és mûveletek Hatványozás. a) 6 ; b),4 4 ; c) (0,6) ; d) () ; e) ;f) 9 9 ;g)b 8 ; h) (y) ;i) c ;j) x.. a) ; b). ; c) 8; d)

Feladatok a szinusz- és koszinusztétel témaköréhez 11. osztály, középszint

TÁMOP-3.1.4-08/-009-0011 A kompetencia alapú oktatás feltételeinek megteremtése Vas megye közoktatási intézményeiben Feladatok a szinusz- és koszinusztétel témaköréhez 11. osztály, középszint Vasvár, 010.

MATEMATIKA TANMENET SZAKKÖZÉPISKOLA 10.B OSZTÁLY HETI 4 ÓRA 37 HÉT/ ÖSSZ 148 ÓRA

MINŐSÉGIRÁNYÍTÁSI ELJÁRÁS MELLÉKLET Tanmenetborító Azonosító: ME-III.1./1 Változatszám: 2 Érvényesség 2013. 09. 01. kezdete: Oldal/összes: 1/7 Fájlnév: ME- III.1.1.Tanmenetborító SZK- DC-2013 MATEMATIKA

Gyakorló feladatok 9.évf. halmaznak, írd fel az öt elemű részhalmazokat!. Add meg a következő halmazokat és ábrázold Venn-diagrammal:

Gyakorló feladatok 9.évf.. Mennyi az összes részhalmaza az A a c; d; e; f halmaznak, írd fel az öt elemű részhalmazokat!. Legyen U ;;;;;6;7;8;9, A ;;6;7; és B ;;8. Add meg a következő halmazokat és ábrázold

Hasonlóság. kísérleti feladatgyűjtemény POKG 2015. 10. osztályos matematika

Hasonlóság kísérleti feladatgyűjtemény 10. osztályos matematika POKG 2015. Hasonló háromszögek oldalaránya 0. Keressük meg az alábbi háromszögek összetartozó oldalpárjait és arányossággal számítsuk ki

MATEMATIKA PRÓBAÉRETTSÉGI 2013 I. rész

MATEMATIKA PRÓBAÉRETTSÉGI 203 I. rész. Oldja meg a következő egyenletet: x 2 25. Az egyenlet megoldása: 2. Egy vállalat 280 000 Ft-ért vásárol egy számítógépet. A számítógép évente 5%-ot veszít az értékéből.

MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT. Koordináta-geometria

MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT 1) Adott két pont: A 4; 1 felezőpontjának koordinátáit! AB felezőpontja legyen F. Koordináta-geometria és B 3 1; Írja fel az AB szakasz 1 3 4

Próbaérettségi feladatsor_a NÉV: osztály Elért pont:

Próbaérettségi feladatsor_a NÉV: osztály Elért pont: I. rész A feladatsor 1 példából áll, a megoldásokkal maximum 30 pont szerezhető. A kidolgozásra 45 perc fordítható. 1. feladat Egy osztály tanulói a

Pitagorasz-tétel. A háromszög derékszögű, ezért írjuk fel a Pitagorasz-tételt! 2 2 2

1. a) Mekkora egy 5 cm oldalú négyzet átlója? Pitagorasz-tétel A háromszög derékszögű, ezért írjuk fel a Pitagorasz-tételt! e 5 5 50 e 50 7,07 cm b) Mekkora egy a oldalú négyzet átlója? e a a a e a. Egy

Osztályozó- és javítóvizsga témakörei MATEMATIKA tantárgyból

Osztályozó- és javítóvizsga témakörei MATEMATIKA tantárgyból 9. évfolyam I. Halmazok 1. Alapfogalmak, jelölések 2. Halmaz, részhalmaz fogalma, részhalmazok száma, jelölések 3. Nevezetes számhalmazok (N,

4. A kézfogások száma pont Összesen: 2 pont

I. 1. A páros számokat tartalmazó részhalmazok: 6 ; 8 ; 6 ; 8. < > < >< >. 5 ( a ) 17 Összesen: t = = a a Összesen: ot kaphat a vizsgázó, ha csak két helyes részhalmazt ír fel. Szintén jár, ha a helyes

Hasonlósági transzformációk II. (Befogó -, magasság tétel; hasonló alakzatok)

Hasonlósági transzformációk II. (Befogó -, magasság tétel; hasonló alakzatok) DEFINÍCIÓ: (Hasonló alakzatok) Két alakzat hasonló, ha van olyan hasonlósági transzformáció, amely az egyik alakzatot a másikba

MATEMATIKA TANMENET. 9. osztály. 4 óra/hét. Budapest, 2014. szeptember

MATEMATIKA TANMENET 9. osztály 4 óra/hét Budapest, 2014. szeptember 2 Évi óraszám: 144 óra Heti óraszám: 4 óra Ismerkedés, év elejei feladatok, szintfelmérő írása 2 óra I. Kombinatorika, halmazok 13 óra

OSZTÁLYOZÓVIZSGA TÉMAKÖRÖK 9. OSZTÁLY

OSZTÁLYOZÓVIZSGA TÉMAKÖRÖK 9. OSZTÁLY ALGEBRA ÉS SZÁMELMÉLET Halmazok Halmazműveletek Halmazok elemszáma Logikai szita Számegyenesek intervallumok Gráfok Betűk használata a matematikában Hatványozás. A

Az osztályozóvizsgák követelményrendszere MATEMATIKA

Az osztályozóvizsgák követelményrendszere MATEMATIKA 1. Számok, számhalmazok A 9. évfolyam során feldolgozásra kerülő témakörök: A nyelvi előkészítő és a két tanítási nyelvű osztályok tananyaga: A számfogalom

5. osztály. Matematika

5. osztály A természetes számok értelmezése 100 000-ig. A tízes számrendszer helyértékes írásmódja. A A természetes számok írásbeli összeadása, kivonása. A műveleti eredmények becslése. Ellenőrzés 3. A

TANMENET. a matematika tantárgy tanításához a 12. E osztályok számára

Az iskola fejbélyegzője TANMENET a matematika tantárgy tanításához a 12. E osztályok számára Készítette: Természettudományi Munkaközösség matematikát tanító tanárai Készült: a gimnáziumi tanterv alapján

Függvények Megoldások

Függvények Megoldások ) Az ábrán egy ; intervallumon értelmezett függvény grafikonja látható. Válassza ki a felsoroltakból a függvény hozzárendelési szabályát! a) x x b) x x + c) x ( x + ) b) Az x függvény

Megyei matematikaverseny évfolyam 2. forduló

Megyei matematikaverseny 0. 9. évfolyam. forduló. különbözı pozitív egész szám átlaga. Legfeljebb mekkora lehet ezen számok közül a legnagyobb? (A) (B) 8 (C) 9 (D) 78 (E) 44. 00 009 + 008 007 +. + 4

Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma) Megoldások

Megoldások 1. Tekintsük az alábbi szabályos hatszögben a következő vektorokat: a = AB és b = AF. Add meg az FO, DC, AO, AC, BE, FB, CE, DF vektorok koordinátáit az (a ; b ) koordinátarendszerben! Alkalmazzuk

MATEMATIKA TANMENET 9.B OSZTÁLY FIZIKA TAGOZAT HETI 6 ÓRA, ÖSSZESEN 216 ÓRA

MATEMATIKA TANMENET 9.B OSZTÁLY FIZIKA TAGOZAT HETI 6 ÓRA, ÖSSZESEN 216 ÓRA A TÁMOP 3.1.4. EU-s pályázat megvalósításához a matematika (9. b/fizika) tárgy tanmenete a matematika kompetenciaterület A típusú

Munkafüzet megoldások 7. osztályos tanulók számára. Makara Ágnes Bankáné Mező Katalin Argayné Magyar Bernadette Vépy-Benyhe Judit

Kalandtúra 7. unkafüzet megoldások 7. osztályos tanulók számára akara Ágnes Bankáné ező Katalin Argayné agyar Bernadette Vépy-Benyhe Judit BEELEGÍTŐ GONDOLKODÁS. SZÓRAKOZTATÓ FELADVÁNYOK. oldal. 6. 6.

352 Nevezetes egyenlôtlenségek. , az átfogó hossza 81 cm

5 Nevezetes egyenlôtlenségek a b 775 Legyenek a befogók: a, b Ekkor 9 + $ ab A maimális ab terület 0, 5cm, az átfogó hossza 8 cm a b a b 776 + # +, azaz a + b $ 88, tehát a keresett minimális érték: 88

MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Koordináta-geometria

MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Koordináta-geometria A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett

Feladatok. 1. a) Mekkora egy 5 cm oldalú négyzet átlója?

Feladatok 1. a) Mekkora egy 5 cm oldalú négyzet átlója? A háromszög derékszögű, ezért írjuk fel a Pitagorasz-tételt! e 5 5 50 e 50 7,07 cm b) Mekkora egy a oldalú négyzet átlója? e a a a e a. Egy négyzet

Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma) Megoldások

Megoldások 1. Írd fel a K (0; 2) középpontú 7 sugarú kör egyenletét! A keresett kör egyenletét felírhatjuk a képletbe való behelyettesítéssel: x 2 + (y + 2) 2 = 49. 2. Írd fel annak a körnek az egyenletét,

Skaláris szorzat: a b cos, ahol α a két vektor által bezárt szög.

1 Összeadás: Legyen a (7; 3) és b (- 2; 4), akkor az összegük a + b (7 + (-2); 3 + 4) = (5; 7) Kivonás: Legyen a (7; 3) és b (- 2; 4), akkor a különbségük a b (7 – (-2); 3-4)=(9; – 1) Valós számmal való

törtet, ha a 1. Az egyszerűsített alak: 2 pont

1. Egyszerűsítse az 3 2 a + a a + 1 törtet, ha a 1. Az egyszerűsített alak: 2. Milyen számjegy állhat az X helyén, ha a négyjegyű 361 X szám 6-tal osztható? X = 3. Minden szekrény barna. Válassza ki az

Az egyes feladatok részkérdéseinek a száma az osztály felkészültségének és teherbírásának megfelelően (a feladat tartalmához igazodva) csökkenthető!

1 Az egyes feladatok részkérdéseinek a száma az osztály felkészültségének és teherbírásának megfelelően (a feladat tartalmához igazodva) csökkenthető! Szerkesztette: Huszka Jenő 2 A változat 1. Az ABCDEFGH

Síkgeometria. Ponthalmazok

Síkgeometria http://zanza.tv/matematika/geometria Ponthalmazok Alapfogalmak: pont egyenes sík (nincs kiterjedése; általában nagy betűvel jelöljük) (végtelen hosszú; általában kis betűvel jelöljük) (végtelen

9. Írjuk fel annak a síknak az egyenletét, amely átmegy az M 0(1, 2, 3) ponton és. egyenessel;

Síkok és egyenesek FELADATLAP Írjuk fel annak az egyenesnek az egyenletét, amely átmegy az M 0(,, ) ponton és a) az M(,, 0) ponton; b) párhuzamos a d(,, 5) vektorral; c) merőleges a x y + z 0 = 0 síkra;

SULINOVA PROGRAMTANTERVÉHEZ ILLESZKEDŐ TANMENET 9. ÉVFOLYAM SZÁMÁRA

1 SULINOVA PROGRAMTANTERVÉHEZ ILLESZKEDŐ TANMENET 9. ÉVFOLYAM SZÁMÁRA Heti óraszám: 3 Éves óraszám: 37 x 3 = 111 A tanmenet 101 óra beosztását tartalmazza. A dolgozatok írása és javítása 10 órát foglal

TARTALOM. Előszó 9 HALMAZOK

TARTALOM Előszó 9 HALMAZOK Halmazokkal kapcsolatos fogalmak, részhalmazok 10 Műveletek halmazokkal 11 Számhalmazok 12 Nevezetes ponthalmazok 13 Összeszámlálás, komplementer-szabály 14 Összeszámlálás, összeadási

, D(-1; 1). A B csúcs koordinátáit az y = + -. A trapéz BD

Kör és egyenes kölcsönös helyzete Kör érintôje 7 9 A húr hossza: egység 9 A ( ) ponton átmenô legrövidebb húr merôleges a K szakaszra, ahol K az adott kör középpontja, feltéve, hogy a kör belsejében van

Kisérettségi feladatsorok matematikából

Kisérettségi feladatsorok matematikából. feladatsor I. rész. Döntse el, hogy a következő állítások közül melyik igaz és melyik hamis! a) Ha két egész szám összege páratlan, akkor a szorzatuk páros. b)

egyenletrendszert. Az egyenlő együtthatók módszerét alkalmazhatjuk. sin 2 x = 1 és cosy = 0.

Magyar Ifjúság. X. TRIGONOMETRIKUS FÜGGVÉNYEK A trigonometrikus egyenletrendszerek megoldása során kísérletezhetünk új változók bevezetésével, azonosságok alkalmazásával, helyettesítő módszerrel vagy más,

A GEOMETRIA TÉMAKÖR FELOSZTÁSA. Síkgeometria Térgeometria Geometriai mérések Geometriai transzformációk Trigonometria Koordináta-geometria

GEOMETRIA A GEOMETRIA TÉMAKÖR FELOSZTÁSA Síkgeometria Térgeometria Geometriai mérések Geometriai transzformációk Trigonometria Koordináta-geometria A SÍKGEOMETRIA TANÍTÁSA 5-10. OSZTÁLY Síkgeometriai fogalmak

MATEMATIKA KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 1I. PRÓBAÉRETTSÉGI FELADATSOR

MATEMATIKA KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 1I PRÓBAÉRETTSÉGI FELADATSOR EGYENES ÚT AZ EGYETEMRE 11 FELADATSOR 11 FELADATSOR I rész Felhasználható idő: 45 perc 6x 1 111) Melyik állítás igaz az alábbi egyenlet

1. Tekintsük a következő két halmazt: G = és H = . Elemeik felsorolásával adja meg a G H és a H \ G halmazokat!

Bevezető matematika kémikusoknak., 04. ősz. feladatlap. Ábrázoljuk számegyenesen a következő egyenlőtlenségek megoldáshalmazát! (a) x 5 < 3 5 x < 3 x 5 < (d) 5 x

Az Országos Középiskolai Tanulmányi Verseny tanévi második fordulójának feladatmegoldásai. x 2 sin x cos (2x) < 1 x.

Az Országos Középiskolai Tanulmányi Verseny 2005-2006. tanévi második fordulójának feladatmegoldásai matematikából, a II. kategória számára 1. Oldja meg a következő egyenlőtlenséget, ha x > 0: x 2 sin