Egyenletek Feladatok Megoldással 9 Osztály
x+\dfracy=6 $” height=”” />
Úton az egyenletek használata felé
Január a középiskolai írásbeli felvételik ideje. Gyermekünk, unokánk, távolabbi rokonunk vagy ismerőseink egyike-másika felvételizik. Hallunk azokról a feladatokról, amelyek kihívást jelentettek számukra.
Előfordulhat, hogy megkérnek, segítsünk a vizsgára való felkészülésben. Az első, hogy megismerkedjünk az elmúlt évek felvételi követelményeivel. Szerencsére 2001 óta a feladatsorok elérhetőek az Oktatási Hivatal honlapján:
Az Érintő 2021. márciusi számában olvashatunk a tavalyi nyolcosztályos, hatosztályos és négyosztályos gimnáziumi felvételik általános értékeléséről.
A hatosztályos gimnáziumok felvételi anyagait tanulmányozva láthatjuk, hogy minden évben előfordulnak olyan szöveges feladatok, amelyeket felnőttként ösztönösen egyenlettel oldanánk meg. Milyen eszközei vannak a hatodik osztályos gyerekeknek ilyen problémák megoldására? A korábbi években a betűs kifejezések használata, nyitott mondatok, egyszerű egyenletek megoldása a hatodik évfolyam második felében szerepelt, tehát már akkor is a felvételi időszak után. Az új NAT bevezetésével ezek a módszerek későbbi évfolyamokra kerültek. Tehát ma az egyenletmegoldás nem a 12 éves diákoktól elvárt rutin. Ők vajon hogyan birkóznak meg a szöveges feladatokkal, mennyire tudnak betűket használni az összefüggések leírására? Logikai következtetéseket használnak? Esetleg egyenletmegoldási módszerekhez hasonlót alkalmaznak? Megfogalmazva a fő kérdést: Tanítsuk meg nekik az egyenletek megoldásának néhány szokásos módszerét a felvételire készülve?
A Kempelen Farkas Gimnázium hatodikos diákjainak feladtunk 8 olyan példát, amelyek az előző 10 év valamelyikében felvételi feladatok voltak. Bizonyos feladatokat órán, másokat otthon oldottak meg szorgalmi feladatként. Az órán egyénileg dolgoztak, otthon több idejük volt a megoldásra, esetleg szülői segítséget is kaphattak. Azt kértük tőlük, hogy megoldásaikat indokolják is, ellentétben a központi írásbeli feladatok követelményeivel, ahol csak a végeredményt kell megadniuk, a javítási útmutató általában ezt értékeli.
Az alábbiakban bemutatunk néhány megoldást a diákok munkáiból. Elemezzük gondolkodásmódjuk sajátosságait, értékeit. Javaslatokat teszünk arra, hogy a felvételi rendszerétől függetlenül a mindennapi tanítási gyakorlatban milyen módszerek megismertetését ajánljuk ebben az életkorban.
Ezeket a feladatokat tanárszakos hallgatók is megoldották, – természetesen egyenlettel – de kérésre adtak más típusú megoldásokat is. Erről is beszámolunk a cikk végén.
A tankönyvek is változatos módszereket kínálnak a szöveges feladatok megoldására, ezekre a tankönyvekre is utalunk a befejezésben.
A feladatokra a kitűzés dátumával és a feladatsorban elfoglalt sorszámukkal fogunk hivatkozni. A megoldásokat nem szó szerint idézzük. A 12 éves gyerek megoldásában sokszor meg kell érezni a mögötte lévő gondolatot, amit esetleg még nem tud korrekt módon szavakba önteni. A cikk olvasója számára érthető formára hoztuk, eközben figyeltünk arra, hogy ne hamisítsuk meg a benne lévő eredeti gondolatot – több feladat esetében a diákmunka fotóját is megadtuk. Többféle megoldás született mindegyik feladat, feladatrész esetében. Megadtuk a feladat megoldását egyenlet alkalmazása nélkül és egyenlet használatával is.
1. (2022. január 22. – 9. feladat)
Anna és Berci lemérte egy téglalap alakú kert három szomszédos oldala hosszának összegét. Az Anna által lemért oldalak hosszának összege 72 méter, a Berci által lemért oldalak hosszának összege 75 méter.
a) Hány méterrel hosszabb a kert hosszabb oldala a rövidebbnél?
b) Hány méter a kert rövidebb oldalának hossza?
c) Hány méter a kert kerülete?
d) Hány négyzetméter a kert területe?
Egy megoldás következtetéssel:
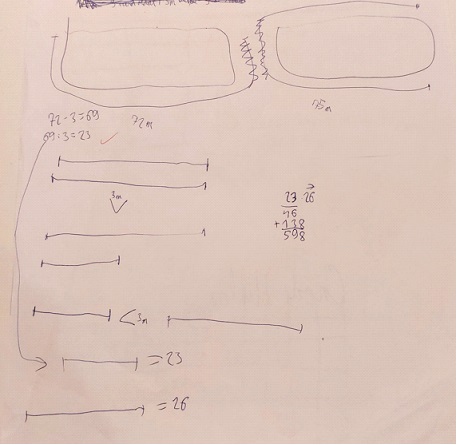
Ebből a leírásból ez a gondolatmenet olvasható ki:
A téglalap két oldala és :
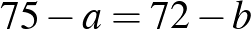
a) Ebből látható, hogy az oldal méterrel nagyobb -nél.
b) Ezért a rövidebb oldal háromszorosa, azaz (m).
c) A hosszabb oldal . A kerület (m)
d) A terület m
Sokan használtak betűket az összefüggések leírására. Néhányan eljutottak az egyenletrendszer megoldásáig is.
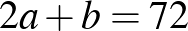
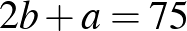
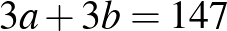
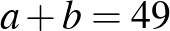
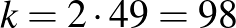
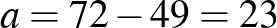
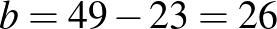
Kicsit „bonyolultabban”:
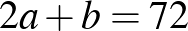
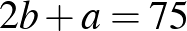
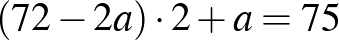
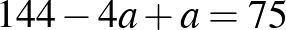
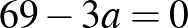
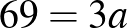
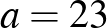
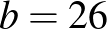
2 . (2020. január 18. – 8. feladat)
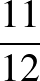
Ezt a megoldást így írhatjuk le a felnőttek nyelvén:
Hétfőn és kedden Hajni 66 feladatot oldott meg helyesen. Ez a feladatok $” height=”” /> része. Ekkor $” height=”” /> rész 6 feladat. Összesen feladattal foglalkozott.
| Hétfő | Hétfőn hibás | Kedd | Kedden hibás | Összesen |
| 12 | 1 | 6 | 0,5 | 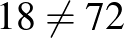 |
| 24 | 2 | 12 | 1 | 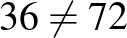 |
| 36 | 3 | 18 | 1,5 | 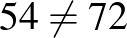 |
| 48 | 4 | 24 | 2 | 72 jó |
Ebből megadható a válasz a kérdésekre.
Következtethetünk
a) Hétfőn a feladatok $” height=”” /> részét megoldotta, $” height=”” /> részét pedig nem.
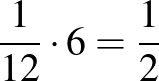
b) A 66 feladatot 2:1 arányban kell felosztani: , tehát 44 feladatot oldott meg helyesen hétfőn.
c) Kedden 22 feladatot oldott meg helyesen. Ez a feladatok $” height=”” /> része. Az $” height=”” /> rész , tehát kedden feladatot nem oldott meg helyesen.
Egyenlettel így dolgozhatunk:
Hétfőn feladat. Megoldva x, $” height=”” /> hibás x$” height=”” />.
Kedden x=\dfracx$” height=”” />. Megoldva \cdot \dfracx=\dfracx$” height=”” />.
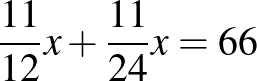
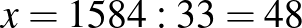
Ebből könnyen megkapjuk a feltett kérdésekre a válaszokat
Két ismeretlennel így jutunk eredményre:
hétfő: 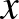 |
helyes 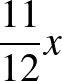 helytelen helytelen 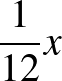 |
kedd: 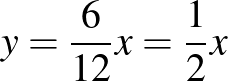 helyes helyes 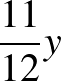 helytelen helytelen 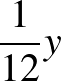 |
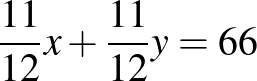
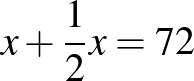
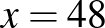
3. (2020. január 23. – 10. feladat)
Az osztály tanulói közül 12-en járnak matematika-szakkörre. 5-tel több fiú nem jár matematika-szakkörre, mint ahány lány jár. Ugyanannyi fiú jár matematika-szakkörre, mint ahány lány nem jár. A lányok közül 2-vel többen járnak matematika-szakkörre, mint ahányan nem járnak.
a) Hány lány jár az osztályba?
b) Hány fiú jár az osztályba?
c) Hány lány jár matematika-szakkörre?
Több jó megoldást találtunk a megoldások között minden indoklás nélkül. Azt tételezzük fel, hogy a gyerekek agyában a megoldáshoz vezető út összetettebb, mint amit ebben a korban meg tudnak fogalmazni. Ha ilyenkor például szakkörön rákérdezünk, akkor szóban körül tudják írni a gondolatmenetüket.
Ilyen gondolkodásra utal, amit ez a gyerek írt:

Láttunk egyenletrendszeres megoldást is:
fiú jár szakkörre, nem jár. Jár szakkörre, nem jár.
A feladat feltételei:
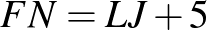
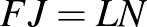
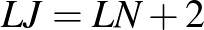
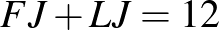
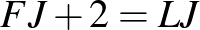
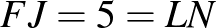
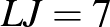
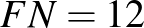
Ilyesmit mutat ez a munka:
Van, aki találgat:
12 szakkörös van. Tudjuk, hogy több lány jár mint fiú. Ez ilyen felosztásban lehetséges:
| LJ | FJ |
| 11 | 1 |
| 10 | 2 |
| 9 | 3 |
| 8 | 4 |
| 7 | 5 |
Csak az utolsó sor adataival nem jutunk ellentmondásra:
; .
…és találkoztunk a felnőttes megoldással is (otthon született), feltételezzük, hogy szülői segítség van mögötte. Táblázatban foglaljuk össze, amit tudunk:
| Jár | Nem jár | |
| L | 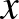 |
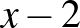 |
| F | 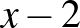 |
 |
| Össz | 12 |
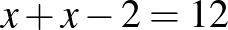
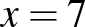
4. (2019. január 24. – 10. feladat)
Peti és az öccse, Marci egy könyvet vásároltak édesanyjuk születésnapjára az édesapjukkal közösen. A két gyerek együtt feleannyit fizetett, mint az édesapa. Peti harmadannyit fizetett, mint az öccse és az édesapja együtt. Marci 1000 Ft-ot fizetett.
a) Az édesapa hányadrészét fizette a könyv árának?
b) Peti hányadrészét fizette a könyv árának?
c) Hány forintot fizetett Peti?
d) Hány forintot fizetett az apa?
e) Hány forintba került a könyv?
A faladatot megoldhatjuk arányos következtetéssel:

A fenti megoldásban ez a gondolat:
Az apa $” height=”” /> -át, Peti $” height=”” /> -ét fizette a könyvnek.
Ha 60 Ft lenne a könyv ára, akkor Peti 15-öt, apa 40-et, Marci 5-öt fizetne. Marci 200-szor annyit, 1000 Ft-ot fizet, ezért Peti Ft-ot, apa Ft-ot fizetett.
A könyv ára így 12 000 Ft.
Van olyan diák, aki betűket használ és egyenletet old meg:
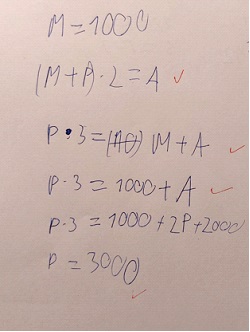
Petinek forintja, Marcinak forintja, édesapjuknak forintja volt: .
Tehát a könyv ára 12 000 Ft.
5. (2016. január 16. – 7. feladat)
Az ábrán négy egyforma céltábla látható. A céltáblákon a lövések helyét pöttyök jelölik. A céltáblák alá odaírtuk, hogy hány pontot érnek összesen a céltáblára érkezett lövések (lásd ábra).
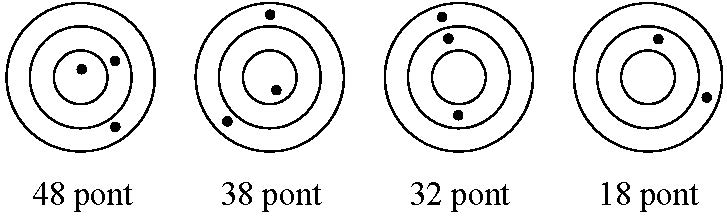
a) Hány pontot ér egy lövés, ha a legbelső körbe esik?
b) Hány pontot ér egy lövés, ha a legkülső sávba esik?
Következtetéssel:
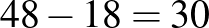
A harmadik és az utolsó ábra alapján a belső tartomány értéke pont.
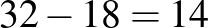
A harmadik és a negyedik ábra alapján a középső tartomány értéke pont.
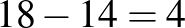
A negyedik ábra alapján a külső tartomány értéke pont.
Ezt a gondolatmenetet egyenletekkel is leírhatjuk:
A belső tartomány pont, a középső pont, a külső tartomány pont.
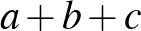 |
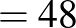 |
( 1 ) |
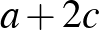 |
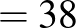 |
( 2 ) |
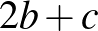 |
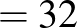 |
( 3 ) |
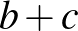 |
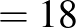 |
( 4 ) |
| (1) – (4) | 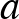 |
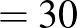 |
| (3) – (4) | 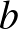 |
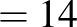 |
| (4) | 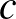 |
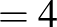 |
Ehhez hasonló gondolatmenetet találtunk ebben a megoldásban is:
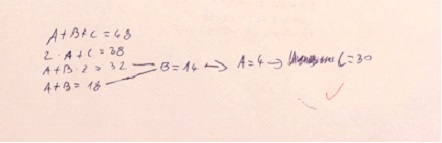
6. (2015. január 17. – 8. feladat)
Jancsi egy tábla csokoládét szeretne venni, de ehhez 60 Ft-ja hiányzik. Ezt a tábla csokit Sanyi sem tudja megvenni, mert 45 Ft-ja hiányzik hozzá. Együtt annyi pénzük van, hogy vehetnek egy ilyen tábla csokoládét, és még marad 10 Ft-juk.
a) Kinek van több pénze és mennyivel?
b) Hány forintba kerül egy tábla csokoládé?
c) Hány forintja van Sanyinak?
A diákok általában egyenletet használtak a megoldáshoz:
A csoki cs forintba kerül:
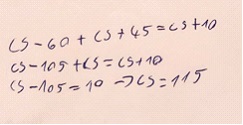
a) Sanyinak 15 forinttal több pénze van.
b) Egy csoki 115 forintba kerül.
c) Sanyinak 70 forintja van.
Ábrával és következtetéssel:
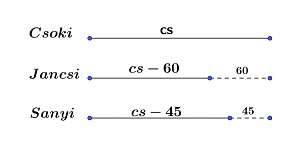
Jancsi pénzéhez Ft-ot kell adnunk, hogy a csoki áránál forinttal többet kapjunk, ezért Sanyinak Ft-ja van. Sanyi pénzéhez forintot kell adni, hogy a csoki áránál Ft-tal többet kapjuk, ezért Jancsinak 55 forintja van. A csoki forintba kerül.
7 . (2014. január 18. –10. feladat)
Dóri, Sári és Anna a legutóbbi, matematikából írt dolgozatukról beszélgettek. A dolgozatukra kapott pontszámaikról a következőket mondták:
Dóri: Hármunk pontjainak összege 258, és nem az enyém lett a legrosszabb hármunk közül.
Anna: Nem az enyém a legjobb, de három ponttal magasabb hármunk pontszámának átlagánál.
Sári: Kettőtök pontjainak összege 30-cal több az én pontszámom kétszeresénél.
a) Kinek lett legkevesebb pontja hármuk közül?
b) Hány pontot kapott a dolgozatára Anna?
c) Hány pontot kapott a dolgozatára Sári?
Hogyan értsük, ha ezt írja egy diák:
 lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” /> lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” /> |
 lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” /> lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” /> |
nem A |
| nem A |  lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” /> lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” /> |
 lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” /> lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” /> |
 lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” /> lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” /> |
 lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” /> lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” /> |
nem S |
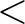
A nagyságrendet úgy írjuk le, hogy írunk két lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” />lt;$” height=”” /> jelet, és beillesztjük a megfelelő információt a megfelelő helyre.
A nem a legnagyobb: … $” height=”” /> … $” height=”” /> nem A (Mert Anna ezt állítja.)
A nem a legkisebb (Mert nagyobb az átlagnál.): nem A $” height=”” /> … $” height=”” /> … (Ebből már következik, hogy A a középső.)
S nem a legnagyobb: … $” height=”” /> … $” height=”” /> nem S (Mert S kisebb, mint A és D átlaga. Ebből már következik, hogy D a legnagyobb.)
Ez alapján . Innen , .
8. (2014. január 23. – 7. feladat)
A könyvesbolt két egyforma hosszúságú polcára egyforma vastagságú mesekönyveket és egyforma vastagságú tankönyveket állítottunk egymás mellé. Az egyik polcot 20 mesekönyvvel és 15 tankönyvvel töltöttük ki, a másikat 12 mesekönyvvel és 27 tankönyvvel.
a) Hány tankönyv vastagsága egyenlő két mesekönyv vastagságával?
b) Hány mesekönyvvel tölthető ki a polc teljesen?
c) Hány centiméter vastag egy tankönyv, ha a polc hossza 90 cm?
Egy gondolat arra, hogy a mesekönyv a vastagabb:

Egy teljes, jó megoldás a gyerekek megoldásaiból összeállítható. De ez így együtt nem szerepelt a dolgozatokban:
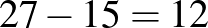
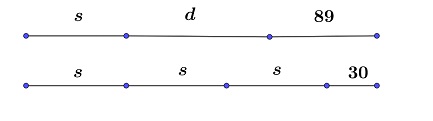
A második polcon tankönyvvel van több.
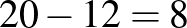
Az első polcon mesekönyvvel van több.
Ezért 12 tankönyv olyan vastag, mint 8 mesekönyv, tehát 3 tankönyv vastagsága egyenlő 2 mesekönyv vastagságával.
Az első polcon a tankönyvet mesekönyvre válthatjuk, ezért a polc szélessége mesekönyvvel vastagságával egyezik meg, egy mesekönyv 3 cm vastag. 2 mesekönyv 6 cm, tehát 1 tankönyv 2 cm vastag.
Egyenletek Feladatok Megoldással 9 Osztály
Elsőfokú egyenletek, megoldási módszereik 6 foglalkozás logikai érték Olyan kijelentő mondat, amelyről egyértelműen el tudjuk dönteni, hogy igaz, vagy hamis, állításnak vagy más néven kijelentésnek nevezzük. A mondattal kapcsolatban az “igaz” vagy “hamis” “tulajdonságot” a mondta logikai értékének nevezzük. Például a “2 prímszám. ” mondat logikai értéke igaz. Tananyag ehhez a fogalomhoz: Mit tanulhatok még a fogalom alapján? igazsághalmaz Egy egyenlet megoldásainak halmazát az egyenlet igazsághalmazának is szokták nevezni. További fogalmak. egyenletek megoldása grafikus úton Egyenlete megoldás egyik módszere. Az egyenlet két oldalát egy-egy függvényként értelmezzük, és közös koordinátarendszerben ábrázoljuk őket. Az egyenlet megoldásai a metszéspont (metszéspontok) x koordinátája (koordinátái). Ha ilyen metszéspont nem létezik, akkor az egyenlet a valós számok halmazán nem oldható meg. A módszer előnye, hogy számos algebrailag nehezen kezelhető egyenlet (pl. log 2 x = |x| – 2) megoldása egész egyszerűvé válik.
Matematika – 9. osztály | Sulinet Tudásbázis
21. századi közoktatás – fejlesztés, koordináció (TÁMOP-3. 1. 1-08/1-2008-0002)
Hátránya viszont, hogy nem egész megoldások esetén, nehéz (sokszor lehetetlen) leolvasni a pontos megoldást. egyenletek megoldása szorzattá alakítással Szorzat értéke akkor és csak lesz 0, ha valamelyik eleme nullával egyenlő. Ezt a törvényt használjuk fel egyenletek megoldásánál: az algebrai kifejezést nullára redukáljuk, szorzattá alakítjuk, és a fentiek szerint járunk el. hamis gyök Ha egy egyenleten nem ekvivalens átalakítást végzünk (például ismeretlent tartalmazók kifejezéssel szorzunk, vagy mindkét oldalát páros kitevőjű hatványra emeljük, stb. ) olyan megoldásokat kaphatunk, amelyek nem megoldásai az eredeti egyenletnek. Ezeket hamis gyököknek nevezzük. Hamis gyökök kiszűrésére a legjobb módszer, az eredeti egyenlet értelmezési tartományának vizsgálata, illetve, mivel ez sokszor egyszerűbb, a kapott eredmény visszahelyettesítéssel történő ellenőrzése. Például oldjuk meg a egyenletet a valós számok halmazán. Beszorozva x-szel beszorozva, majd elvéve x-et mindkét oldalból kapjuk, hogy x = 0.
Egyenletek megoldása feladatok
Az előzőekben adott egyenletek megoldásával foglalkoztunk. Az egyenletek megoldása azonban nem öncélú. Sokféle munkahely, a technika, a tudomány, a gazdasági élet olyan problémákat vet fel, amelyek megoldása először egyenletek felírását (matematikai modell felállítását), majd azok megoldását kívánja.
Feladat: szövegből egyenlet
11. példa: Laboratóriumban nagy mennyiségben van 28%-os és 63%-os oldat. Nekünk 14 liter 43%-os oldatra van szükségünk. Melyikből mennyit vegyünk ki, hogy azokat összeöntve 14 liter 43%-os oldatot kapjunk?
Megoldás: szövegből egyenlet
Jelöljük x-szel azt a mennyiséget, amit a 28%-os oldatból veszünk ki. Mivel 14 literre van szükségünk, a másikból (14 – x) liter kell. (Most előre tudjuk, hogy a 28%-os oldatból többet kell kivennünk, mint a 63%-osból, mert 43%-ost kell kapnunk, és az „közelebb” van a 28%-oshoz, mint a 63%-oshoz.)
Írjuk fel a számadatokat áttekinthetően:
A két oldat összeöntésekor az oldatokban levő feloldott anyagok, azaz a tömény részek összegződnek. Ezért az összeöntött két oldat tömény részének az összege azonos a kívánt keverék tömény részével:
A 28%-os oldatból 8, a 63%-os oldatból 6 litert kell kivennünk és összeöntenünk, ekkor kapunk 14 liter 43%-os oldatot.
Másodfokú egyenlet megoldóképlete, gyöktényezős alak, Viète-formulák

A másodfokú egyenletek a középiskolai tanulmányok szerves részét képezik. A közép- és az emelt szintű érettségin is rendszeresen szerepel olyan feladat, mely másodfokú egyenlet megoldását igényli. Ezért nagyon fontosak az ilyen tipusú egyenletekkel kapcsolatos ismeretek.
Ebben a cikkben definiáljuk a másodfokú egyenletet, levezetjük a megoldóképletét. Továbbiakban megadjuk a diszkrimináns fogalmát és megvizsgáljuk, hogy mitől függ a másodfokú egyenlet valós megoldásainak száma.
Megismerkedünk a másodfokú polinom gyöktényezős alakjával és Viète-formuláival. Ezek már az emelt szintű érettségi témaköreihez tartoznak.
Ha szeretnéd az elméletet gyakorlatban alkalmazni, akkor ajánljuk figyelmedbe a Feladatok másodfokú egyenletekre alapoktól az emelt szintig című cikkünket, melyet ITT lehet elérni.
Kinek hasznos az alábbi cikkünk?
Neked, ha érettségire készülsz, és át szeretnéd ismételni a másodfokú egyenletekkel kapcsolatos ismereteidet.
Neked, ha szeretnél jártasságot szerezni a másodfokú egyenletekkel kapcsolatos feladatok megoldása terén.
Neked, ha esetleg már régebben voltál iskolás, ugyanakkor valamiért most szükséged lenne a másodfokú egyenlet megoldásával kapcsolatos ismeretekre, és szeretnéd feleleveníteni azokat.
Mi segítünk! Olvasd el cikkünket, és megtalálod a választ kérdéseidre.
A másodfokú egyenlet definíciója
alakú egyenletet egyismeretlenes másodfokú egyenletnek nevezzük, ahol a, b, c valós számok és a nem lehet 0.
Az x az ismeretlen, az a, a b és a c pedig az együtthatók.
ahol az együtthatók
A másodfokú egyenlet megoldóképlete
Két példa a teljes négyzetté kiegészítésre
A másodfokú egyenleteket megoldhatjuk például teljes négyzetté kiegészítéssel. Erre lássunk most két példát!
Megoldás: Egészítsük ki teljes négyzetté a bal oldali kifejezést:
Alkalmazzuk a kapott kifejezésre a két tag négyzetének különbségére vonatkozó összefüggést, azaz az
egyenlethez jutottunk, melynek megoldásai
hisz egy szorzat pontosan akkkor 0, ha valamelyik tényezője 0. Ezzel az egyenletet megoldottuk.
Megoldás: Ebben az esetben is alakítsuk teljes négyzetté az egyenlet bal oldalát! Kezdjük azzal, hogy kiemeljük a másodfokú tag együtthatóját!
Megint alkalmazzuk a két tag négyzetének különbségére vonatkozó azonosságot:
egyenlet megololdásával megkapjuk az eredet egyenlet megoldásait.
Itt újfent kihasználtuk, hogy egy szorzat pontosan akkor 0, ha valamelyik tényezője 0.
A másodfokú egyenlet megoldóképlete
Az előző két példában tárgyalt teljes négyzetté kiegészítés módszerével mindig megoldhatjuk a másodfokú egyenleteket, ugyanakkor ez így nehézkes és hosszadalmas. Szerencsés lenne egy olyan eszközzel rendelkezni, mellyel egyszerűen és gördülékenyen megkaphatjuk a másodfokú egyenletek valós mgoldásait, feltéve, hogy léteznek.
Erre szolgál a másodfokú egyenlet megoldóképlete, amely összefüggést termet az egyenletben szereplő együtthatók és az egyenlet megoldásai között.
Tétel: Az
másodfokú egyenlet megoldásait az
képlettel számolhatjuk ki.
Ha a diszkrimináns, azaz a
kifejezés értéke pozitív, akkor két különböző valós megoldása van az egyenletnek, ha nullával egyenlő, akkor egy, ha negatív, akkor nincs valós megoldása a másodfokú egyenletnek.
Bizonyítás: A tétel bizonyítása a konkrét példában is látott teljes négyzetté kiegészítésen alapul. Ezért is foglalkoztunk ezzel a módszerrel az előző két feladatban. A részletes bizonyítást az alábbi videóban találja meg az érdeklődő olvasó.
A másodfokú egyenlet megoldóképletének levezetése
A másodfokú egyenlet gyöktényezős alakja és Viète-formulái
A másodfokú egyenlet gyöktényezős alakja
Az egyenletek, a számelméleti problémák, az algebrai kifejezések világában nagyon fontos, hogy minél hatékonyabban tudjunk szorzattá alakítani.
Ebben az alpontban megismerkedünk a
másodfokú polinomok szorzattáalakításának egy gyors és könnyen alkalmazható módszerével.
Megoldás: Ezt a feladatot lényegében már megoldottuk a 2. példában, hisz az ott szereplő egyenlet megoldásait szorzattá alakítással kerestük meg.
Most elevenítsük fel az ott látottakat:
Ezzel a feladatot megoldottuk.
A két zárójeles kifejezés második tagjában szereplő számok a 2 és a 2/3. Ezek a
Ez azt sugallja számunkra, hogy a
másodfokú polinom szorzattá alakításánál úgy is eljárhatunk, hogy megoldóképlettel meghatározzuk az
valós megoldásait, feltéve, hogy léteznek és behelyettesítjük azokat az
kifejezésbe. Ezt az alakot nevezzük a másodfokú polinom gyöktényezős alakjának.
Az erre vonatkozó bizonyítást lásd alább, a következő alfejezetben található videóban.
Viète-formulák
A másodfokú egyenlet megoldóképlete egy összefüggés az egyenletben szereplő együtthatók és az egyenlet megoldásai között. Az emelt szintű érettségire készülők találkozhatnak olyan problémákkal, melyek megoldásánál szükség van az egyenlet gyökei és együtthatói közötti összefüggésre, ugyanakkor a megoldóképlet használata túlságosan bonyolulttá teszi a megoldást.
Ilyenkor nyújtanak hatékony segítséget a Viète-formulák, vagy más néven a másodfokú egyenlet gyökei és együtthatói közötti összefüggések.
Tétel: Legyen adott a
másodfokú polinom, melyre teljesül, hogy
Ekkor a polinom gyökeire fennáll az
össszefüggés. Ezeket nevezzük a másodfokú polinom Viète-formuláinak.
A gyöktényezős alakra, illetve a Viète-formulákra vonatkozó tétel bizonyítása az alábbi videóban látható.
A másodfokú polinom gyöktényezős alakja és Viète-formulái
Összefoglalás
Az előző cikkben megismerkedtünk a másodfokú egyenlet definíciójával, majd levezettük az egyenlet megoldóképletét. Definiáltuk az egyenlet diszkriminánsát és megnéztük hogyan függ annak előjelétől az egyenlet valós megoldásainak száma.
Az emelt szintű témakörök közül foglalkoztunk a másodfokú polinom gyöktényezős alakjával és Viète-formuláival.
Ha valaki szetné elmélyíteni az elméleti ismereteket, akkor annak ajánlom figyelmébe a Feladatok másodfokú egyenletekre alapoktól az emelt szintig című cikkünket, melyet ITT lehet elérni.
Szeretnél még több, hasonló cikket olvasni? Akkor böngéssz a blogunkon Matekos blog!
Ha emelt szintű érettségire készülsz, vagy elsőéves egyetemista vagy? Ekkor ajánljuk figyelmedbe az online tanuló felületünket és a felkészülést segítő csomagjainkat. Az ezekkel kapcsolatos részletekről itt ÉrettségiPro+ olvashatsz.
Összegyűjtöttük az eddigi összes emelt szintű matematika érettségi feladatsort és a megoldásokat. Ezt a gyűjteményt, valamint az érettségire készüléssel kapcsolatos hasznos tanácsokat a Emelt szintű matematika feladatsorok linken érheted el.
A szerző további cikkei megtalálhatók a Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium matematika portálján ezen a linken.
Comments are closed, but trackbacks and pingbacks are open.