Függvény egyenletmegoldás

Ábrázoljuk az egyenlet bal és jobb oldalának a függvényeit ugyanabban a koordináta-rendszerben. A két grafikus kép közös pontjainak leolvassuk az x koordinátáit. Ezek az egyenlet gyökei, hiszen ezeknél az értékeknél a bal oldal és a jobb oldal függvényértékei egyenlőek.

Harmadfokú egyenlet megoldása

Elsősorban ez az oldal egyismeretlenes harmadfokú egyenlet megoldó kalkulátorát tartalmazza. A harmadfokú függvény ismertetése és a megoldó képlete a kalkulátor alatt található.

Első lépés, hogy a függvényt ilyen formába hozod: a·x³+b·x²+c·x+d=0

x1=

x2=

x3=

Mi a harmadfokú függvény?

Harmadfokú függvény egy harmadrendű polinom mely 4 együtthatóból áll (a, b, c, d), az összefüggés leírható következő általános képlettel:

`f(x) = a*x^3+b*x^2+c*x+d` , ahol a, b, c és d konstansok, x pedig a változó érték.

A fenti képletnek zérushelyeit keresve, meg kell határozni azt az x értéket (vagy értékeket), melyekkre f(x)=0.

Tehát az egyismeretlenes harmadfokú egyenlet általános képlete: `a*x^3+b*x^2+c*x+d=0` ahol `a!=0`, (mivel akkor nem lenne harmadfokú az egyenlet)

Harmadfokú egyenlet ábrázolva nagyon hétköznapi nyelvvel leírva egy görbe ami három irányba is haladhat (például nő, csökken, nő). Így a görbének lehetősége van akár 3x is átmetszeni a vízszintes tengelyt, ilyenkor 3 megoldás van az x-re.

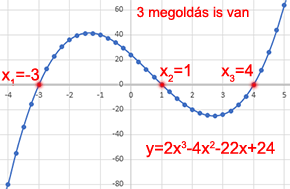
Kalkulátorban megnézhetik a fenti egyenletet, ha a=2, b=-4, c=-22, d=24 akkor x₁=-3, x₂=1, x₃=4 eredmények jönnek ki.

De néha kétszer is irányt vált, úgy hogy nem éri el az x tengelyt, akkor csak 1 megoldás van (valós számok tartományában):

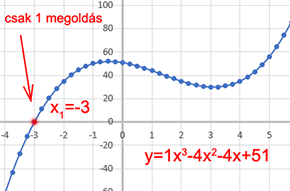
Ha a fenti képletet beírják a kalkulátorba: a=1, b=-4, c=-4, d=51, akkor x₁=-3 eredmény jön ki, csak egy megoldás van.

Harmadfokú egyenlet megoldó képlete

Huhh, ezt most nagyon lerövidítem, bár így is hosszúnak nézhet ki.

`a*x^3+b*x^2+c*x+d=0` általános alakú egyenletben következő helyettesítést alkalmazunk: `x=-b/(3*a)+X`

ekkor következő formára hozható a képlet:

ahol legyen A az X szorzója, B a konstans:

így a következő egyenletet kapjuk:

`X^3+A*X+B=0` és ennek az egyenletnek keressük a gyökeit (milyen X-re (nagy X) lesz nulla az egyenlet értéke).

. most itt átugrok pár sort a levezetésből, és a lényegre térek. (amit átugórtam, forrásban megtekinthető [1])

A megoldóképlet diszkrimináns (Δ) értéke:

Ha Δ>=0, akkor egy valós megoldása lesz az egyenletnek:

[1]: Nickalls, R. W. D. (July 2006), Viète, Descartes and the cubic equation (PDF 438 kB), Mathematical Gazette, 90: oldalak 203–208, hozzáférve 2017-01-17.
Megjegyzés: Sajnos a kerekítési pontatlanság itt gyakori, mivel nagyon sok a “lebegőpontos” és trigonometriai művelet (cos, arccos). Minden műveletnél a kerekítési pontatlanság növekszik. Ezért is építettem be a végeredmény-ellenőrző részt a kalkulátorba. De pl. 10 -10 = 0,0000000001, az majdnem 0.
Képletek megjelenítésére mathjax.org skriptet használtam.

Középiskolai matek (teljes)

Ezt a nagyon laza Középiskolai matek (teljes) kurzust úgy terveztük meg, hogy egy csapásra megértsd a lényeget. Tudásszinttől függetlenül, teljesen az alapoktól magyarázzuk el a tananyagot, a saját ritmusodban lépésről lépésre. Így tudjuk a legbonyolultabb dolgokat is elképesztően egyszerűen elmagyarázni.

Ez nekem is kell

HALMAZOK ÉS GRÁFOK

– Mik azok a halmazok? Halmazok metszete, uniója, különbsége, részhalmazok, műveletek halmazokkal. – Mik azok a gráfok? Élek, csúcsok, utak, fa, egyszerű gráfok, fokszám, feladatok gráfokkal.

FÜGGVÉNYEK

– Lássuk hogyan kell ábrázolni a másodfokú függvényeket. Megnézzük, hogy mi az a teljes négyzetté kiegészítés. – Itt jönnek a gyökös függvények. Megnézzük, hogyan kell ábrázolni őket. – Lássuk, milyen az abszolútérték függvény. – Megnézzük a reciprok függvényt, vagyis az 1/x függvényt, amelynek grafikonja a hiperbola. – Itt jönnek az exponenciális függvények. – A logaritmus függvények áttekintése. – Megnézzük, hogy melyik függvény hogyan néz ki, aztán megnézzük a külső és belső függvénytranszformációkat. Eltolás az x tengely mentén, eltolás az y tengely mentén, tükrözés, nyújtás.

MÁSODFOKÚ EGYENLETEK, EGYENLETRENDSZEREK

– Elsőfokú egyenletek megoldása, a mérleg elv. Törtes egyenletek megoldása. – Másodfokú egyenletek megoldása, a másodfokú egyenlet megoldóképlete, törtes egyenletek, másodfokúra vezető egyenletek megoldása, egyenletrendszerek.

EGYENLŐTLENSÉGEK

– Hogyan kell megoldani egyenlőtlenségeket? Mi a különbség egyenletek és egyenlőtlenségek megoldási módszerei között? Egyenlőtlenségek megoldása számegyenesen előjel ábrázolással. – Itt jön néhány izgalmas feladat, ahol gyakoroljuk az egyenlőtlenségek megoldását.

ABSZOLÚTÉRTÉKES EGYENLETEK

• Abszolútértékes egyenletek megoldása – Mi az abszolútérték? Mik azok az abszolútértékes egyenletek? Abszolútértékes egyenletek megoldása. Abszolútértékes egyenlőtlenségek megoldása.
• Újabb abszolútértékes egyenletek – Itt néhány igazán remek abszolútértékes egyenletet oldunk meg.

EXPONENCIÁLIS EGYENLETEK

• Hatványazonosságok – Készítünk egy szuper-érthető összefoglalót a hatványazonosságokból. Megnézzük, hogyan kell a hatványazonosságokat használni. Megnézzük mi az az exponenciális függvény és hogyan kell ábrázolni.
• Exponenciális egyenletek megoldása – Mik azok az exponenciális egyenletek? Hogyan kell megoldani egy exponenciális egyenletet? Törtes exponenciális egyenletek. Másodfokú egyenletre vezető exponenciális egyenletek.

LOGARITMIKUS EGYENLETEK

• Mi az a logaritmus? – Itt végre szuper-érthetően kiderül, hogy mi az a logaritmus. Készítünk egy gyors kis összefoglalót a logaritmus azonosságairól. Megnézzük, hogyan kell a logaritmus azonosságokat használni. Megnézzük mi az a logaritmus függvény és hogyan kell ábrázolni.
• Logaritmusos egyenletek megoldása – Mik azok a logaritmusos egyenletek? Hogyan kell megoldani egy logaritmikus egyenletet? Milyen kikötéseket kell tenni egy logaritmusos egyenlet megoldásánál? Törtes logaritmikus egyenletek. Másodfokú egyenletre vezető logaritmikus egyenletek.

GYÖKÖS EGYENLETEK

• Gyökös azonosságok – Készítünk egy szuper-érthető összefoglalót a gyökös azonosságokról. Megnézzük, hogyan kell az azonosságokat használni, milyen kikötéseket kell tenni a gyökös kifejezéseknél, hogyan néz ki a gyök függvény.
• Gyökös egyenletek megoldása – Megnézzük, hogy milyen izgalmak fordulhatnak elő a gyökös egyenletek világában. Hogyan kell megoldani egy gyökös egyenletet? Mikor lehet egy egyenletet négyzetre emelni? Milyen kikötéseket kell tenni egy gyökös egyenlet megoldásánál? Törtes gyökös egyenletek. Másodfokú egyenletre vezető gyökös egyenletek.

TRIGONOMETRIKUS EGYENLETEK

• Az egység sugarú kör – Mi az egység sugarú kör? Mi az a szinusz és koszinusz? Mire jó a szinusz és a koszinusz? Mi az a radián? Mi a kapcsolat a fok és a radián között?
• Szinusz, koszinusz – A szinusz és koszinusz definíciója egység sugarú körben. Nevezetes szögek szinusza és koszinusza. Trigonometrikus azonosságok. Trigonometrikus egyenletek megoldása.

A TELJES INDUKCIÓ

• Mi az a teljes indukció? – Megnézzük, hogyan működik a teljes indukció és mik a teljes indukciós bizonyítás lépései. Mi az az indukciós feltevés? Hogyan lehet végtelen sok állítást három lépésben igazolni. Teljes indukciós feladatok. Teljes indukciós egyenlőtlenségek.

SZÁMTANI ÉS MÉRTANI SOROZATOK

• A számtani sorozat – Megnézzük a számtani sorozat általános tagjának képletét, valamint a számtani sorozat összegképletét.
• A mértani sorozat – Itt jön a mértani sorozat általános tagjának kélete és a mértani sorozat összegképlete.
• Minden, amit a számtani és mértani sorozatokról tudni kell– Szuper-érthetően kiderül, hogy mik azok a számtani és mértani sorozatok és mire lehet őket használni. Megnézzük a számtani sorozat általános tagjának képletét, valamint a számtani sorozat összegképletét. Aztán jön a mértani sorozat általános tagjának kélete és a mértani sorozat összegképlete. Feladatok számtani sorozatokkal. Feladatok mértani sorozatokkal. Vegyes feladatok számtani és mértani sorozatokra.

SÍKGEOMETRIA

• Szinusz és koszinusz a síkgeometriában – Megnézzük, hogy derékszögű háromszögekben mit jelent a szinusz és a koszinusz. Mire jó a szinusz és a koszinusz, mire lehet használni? Geometriai feladatok megoldása szinusz és koszinusz szögfüggvények segítségével.
• Szinusz derékszögű háromszögekben – Egy derékszögű háromszögben a szöggel szemközti befogó és az átfogó arányát a szög szinuszának nevezzük.
• Koszinusz derékszögű háromszögekben – Egy derékszögű háromszögben a szög melletti befogó és az átfogó arányát a szög koszinuszának nevezzük.
• Háromszögek nevezetes vonalai és pontjai – Megismerkedünk a háromszögek nevezetes vonalaival és pontjaival. Megnézzük, hogy mi az a magasságvonal és mi a magasságpont. Megnézzük, hogy mi az a súlyvonal és mi a súlypont. Megnézzük, hogy mi az oldalfelező merőleges és a szögfelező és kiderül, hogy melyik pont a háromszög köré írható kör valamint a háromszögbe írható kör középpontja. Nézünk különböző területképleteket háromszögekre, végül jön néhány trapéz is.

SZINUSZTÉTEL ÉS KOSZINUSZTÉTEL

• A szinusztétel és a koszinusztétel – A derékszögű háromszögekben használt szinusz és koszinusz fogalmát átültetjük általános háromszögekre két nagyon izgalmas tétel segítségével. Az egyik a szinusztétel, a másik a koszinusztétel. Megnézzük, hogy mikor érdemes a szinusztételt és mikor érdemes a koszinusztételt használni. Szinusztételes feladatok. Koszinusztételes feladatok. Vegyes feladatok szinusztétellel és koszinusztétellel.
• Mikor használjuk a szinusztételt? – Itt jön néhány példa arra, hogy mikor használjuk a szinusztételt.
• Mikor használjuk a koszinusztételt? – Megnézzük, hogy mi az a koszinusztétel és mikor érdemes használni.

TÉRGEOMETRIA

• Gúlák és hasábok – Itt térgeometriai izgalmak kezdődnek. Megnézzük, hogy mi a gúla és mi a hasáb, mit jelent a palást és az is kiderül, hogy hogyan kell kiszámolni a gúlák és hasábok térfogatát és felszínét. Aztán nézünk néhány feladatot gúlákra és hasábokra, hengerekre és kúpokra. Megnézzük azt is, hogy egy test méreteinek változtatásával a felszíne négyzetesen, a térfogata pedig köbösen változik.
• Gúlák térfogata – Lássuk, hogyan kell kiszámolni a gúlák térfogatát.
• Gúlák felszíne – Nézzük, hogyan kell kiszámolni a gúlák felszínét.
• Hasábok térfogata – Lássuk, hogyan kell kiszámolni a hasábok térfogatát.
• Hasábok felszíne – Na és itt jön a hasábok felszíne.
• Kúpok és hengerek térfogata és felszíne – Megnézzük, hogy mi a kúp és a henger, mit jelent a palást és az is kiderül, hogy hogyan kell kiszámolni a kúpok és hengerek térfogatát és felszínét. Aztán nézünk néhány feladatot hengerekre és kúpokra.

KOORDINÁTAGEOMETRIA

• Vektorok – Műveletek vektorokkal, vektorok hossza, vektorok forgatása, skaláris szorzat, merőleges vektorok és más izgalmak.
• Az egyenes egyenlete – Mi az normálvektor? Mi az irányvektor? Egyenes egyenletének felírása, pont és egyenes távolsága, párhuzamos és merőleges egyenesek.
• Pont és egyenes távolsága – Egyenes egyenletének felírása, pont és egyenes távolságának kiszámolása, képlet pont és egyenes távolságára.
• Párhuzamos egyenesek távolsága – Megnézzük, hogyan lehet kiszámolni az egyenesek egyenleteinek ismeretében az egyenesek távolságát.
• A kör egyenlete – Hogyan írjuk föl egy kör egyenletét? A kör kanonikus egyenlete, a kör középpontja és sugara, kör és egyenes metszéspontja.
• Vegyes feladatok körökkel és egyenesekkel – Kör és egyenes metszéspontja, kör érintője, párhuzamos és metsző egyenesek.

KOMBINATORIKA

• Kombinatorikai összefoglaló – Mik ezek és mire lehet őket használni? Kombinatorika feladatok megoldása lépésről-lépésre. Permutációkkal kapcsolatos feladatok, variációkkal kapcsolatos feladatok, kombinációval kapcsolatos feladatok, ismétléses permutáció, ismétléses variáció.
• Permutáció – Példák ismétlés nélküli és ismétléses permutációkra.
• Variáció – Lássuk, hogy mi az ismétlés nélküli és az ismétléses variáció.
• Permutáció – Példák ismétlés nélküli és ismétléses permutációkra.
• Kombináció – Izgalmas feladatok kombinációkkal.

VALÓSZÍNŰSÉGSZÁMÍTÁS

• Kedvező per összes – Megnézzük, hogyan kell események valószínűségét kiszámolni. A kedvező/összes elv. Valószínűségszámítás feladatok megoldással.
• Események– Mik azok az események? Mik az elemi események? Hogyan kell kiszámolni a valószínűségüket?
• Független és kizáró események – Mit jelent az, hogy két esemény független? Mit jelent az, hogy kizárók?

STATISZTIKA

• Mi az amit statisztikából tudni kell? – Itt kiderül, hogy mi az a módusz és mi a medián, hogyan kell átlagot és szórást számolni. Megnézzük, hogy mi a súlyozott átlag, hogyan kell kiszámolni. Készítünk oszlopdiagramot, kördiagramot, hisztogramot, és megnézzük mire jók ezek valójában.
• Módusz – Ez a leggyakoribb érték. Nade mi is az, és hogyan kell kiszámolni?
• Medián – A medián a sorba rendezett adatsor középső értéke. De mi is ez pontosan?
• Átlag, súlyozott átlag – Lássuk, mi az átlag és mi a súlyozott átlag.
• Szórás – Egy nagyon izgalmas dolog: a szórás.

Algebra, nevezetes azonosságok

Az összeadás, kivonás, szorzás, osztás, hatványozás és zárójelezések műveleti sorrendjei.

Hogyan végezzünk műveleteket betűs kifejezésekkel.

Itt jön néhány példa arra, hogyan lehet kiemeléssel szorzattá alakítani.

Ha a törtekből nem lett volna elég, itt jönnek az algebrai törtek.

Törtek és algebrai törtek egyszerűsítésének módszerei.

Kéttagú összegek és különbségek négyzetre emelése. Két négyzet különbségének szorzata.

Kéttagú összegek és különbségek köbre emelése.

Kéttagú összegek n-edik hatványra emelésének képlete.

Az (a+b) hatványainak általánosítására egy képlet.

Egy kifejezés értelmezési tartományán azt a legbővebb halmazt értjük, ahol értelmezve van.

Halmazok

Az A és B halmazok uniója: Azon elemek halmaza, amelyek legalább az egyik halmazban benne vannak. Az A és B halmazok metszete: Azon elemek halmaza, amelyek mindkét halmazban benne vannak. Az A és B halmazok különbsége: Azon elemek halmaza, amelyek az A halmazba benne vannak, de a B halmazba nem. Az A halmaz komplementere a H alaphalmazon nézve: Az alaphalmaz azon elemeinek halmza, amelyek nincsenek benne az A-ban.

A logikai szita formula a halmazok elemszámának meghatározását segítő képlet.

Az első De Morgan azonosság azt mondja, hogy a metszet komplementere pont megegyezik a komplementrek uniójával. A második De Morgan azonosság pedig azt mondja, hogy az unió komplementere éppen megegyezik a komplementerek metszetével.

Egy halmaz összes részhalmazainak halmazát hatványhalmaznak nevezzük.

Az A és B halmazok Descartes-szorzata úgy működik, hogy elkészítjük az összes lehetséges rendezett párt, aminek az első elemét A-ból, a második elemét pedig B-ből vesszük, és ezeket a rendezett párokat betesszük egy halmazba.

Az f halmazt függvénynek nevezzük, ha minden eleme rendezett pár és minden x-hez csak egy y tartozik.

Gráfok

A gráf egy csúcsának fokszáma a gráf e csúcsában összefutó élek száma.

Egy gráf egyszerű, ha nincs benne sem többszörös él, sem hurokél.

Ha egy gráfban nincs kör, de maga a gráf összefüggő, akkor fának nevezzük.

A gráf csúcsokból és azokat összekötő élekből áll.

Egy gráfban körnek nevezünk egy olyan utat, amely csupa különböző csúcsokon és éleken haladva visszavezet a kiinduló csúcsába.

Egy gráf összefüggő, ha bármelyik csúcsából el lehet jutni bármelyik másik csúcsába élek mentén.

Azokat a gráfokat, ahol minden csúcs mindegyikkel össze van kötve, teljes gráfnak hívjuk.

Egy gráf Euler-köre olyan zárt élsorozat, amely a gráf összes élét pontosan egyszer tartalmazza.

Bizonyítási módszerek, matematikai logika

Az állítás (vagy kijelentés) olyan kijelentő mondat, amelyről egyértelműen eldönthetjük, hogy az igaz vagy hamis.

Az egzisztenciális kvantor egy jelölése a “létezik” vagy “van olyan” kifejezésnek.

Egy $A$ kijelentés negációja az a kijelentés, amely akkor igaz, ha $A$ hamis és akkor hamis, ha $A$ igaz.

Az univerzális kvantor egy jelölése a “minden” kifejezésnek.

Két kijelentés diszjunkciója pontosan akkor igaz, ha legalább az egyik kijelentés igaz, különben hamis.

Az ekvivalencia akkor igaz, ha $A$ és $B$ logikai értéke azonos, különben hamis.

Az implikáció akkor hamis, ha $A$ igaz és $B$ hamis, minden más esetben igaz.

Két kijelentés konjunkciója pontosan akkor igaz, ha mindkét kijelentés igaz, különben hamis.

De Morgan azonosságok a konjunkció, diszjunkció, implikáció és ekvivalencia tagadásaira.

Számelmélet

10-zel azok a számok oszthatók, amik 0-ra végződnek.

11-gyel azok a számok oszthatók, amik egy nagyon vicces dolgot tudnak.

Egy szám akkor osztható 2-vel, ha páros.

Egy szám akkor osztható 3-mal, ha a számjegyeinek összege osztható 3-mal.

Egy szám akkor osztható 4-gyel, ha az utolsó két jegyéből alkottot szám osztható 4-gyel.

Egy szám akkor osztható 5-tel, ha az utolsó számjegye 0 vagy 5.

6-tal azok a számok oszthatók, amik 2-vel és 3-mal is oszthatók.

Egy szám akkor osztható 9-cel, ha a számjegyeinek összege osztható 9-cel.

Ha egy természetes számot osztunk egy másik nem nulla természetes számmal és az nincs meg benne egésszer, akkor maradék is lesz.

Mit jelent az, hogy egy szám osztója egy másik számnak.

Két számok legnagyobb közös osztója az a szám, amelyik mindkét számot osztja és ezek közül a legnagyobb.

Néhány izgalmas oszthatósági szabály.

Két szám relatív prímek, ha a legnagyobb közös osztójuk 1.

Azokat a pozitív egész számokat, amelyeknek az 1-en és önmagukon kívül nincsen más pozitív egész osztója, prímeknek nevezzük.

A nullától és az egytől különböző összes $n$ pozitív egész szám felbontható prímek szorzatára a sorrendtől eltekintve egyértelműen.

A legkisebb közös többszörös megtalálásának lépései.

A tizes számrendszerbe való átváltás lépései.

A kettes számrendszerbe átváltáshoz elkezdjük a számot 2-vel maradékosan osztogatni, amíg már csak a 0 marad.

Elsőfokú egyenletek

Elsőfokú egyenletek megoldása, a mérleg elv. Törtes egyenletek megoldása.

Elsőfokú függvények

A lineáris függvények, azaz egyenesek ábrázolása és jellemzése.

Függvények ábrázolása

Azon x-ek halmaza, amik részt vesznek a hozzárendelésben.

A függvény egy egyértelmű hozzárendelés.

Olyan hozzárendelés, ami különböző x-ekhez különböző y-okat rendel.

Azokat a pontokat, ahol a függvény grafikonja az x tengelyt metszi, zérushelynek nevezzük.

A függvény konvexitása megmondja, hogy a függvény szomorú vagy vidám hangulatban van.

A függvény monotonitása lehet növekedő, csökkenő, szigorúan monton növekedő vagy szigorúan monoton csökkenő.

Globális és lokális maximumok és minimumok.

Megnézzük, hogy melyik függvény hogyan néz ki, aztán megnézzük a külső és belső függvénytranszformációkat. Eltolás az x tengely mentén, eltolás az y tengely mentén, tükrözés, nyújtás.

Mikor páros, mikor páratlan vagy éppen egyik sem egy függvény.

Lássuk mik azok a polinomfüggvények, és hogyan kell őket ábrázolni.

Másodfokú egyenletek

A másodfokú egyenlet megoldóképletének gyök alatti része a diszkrimináns.

A másodfokú egyenlet megoldóképlete és alkalmazása.

A másodfokú egyenlet szorzatalakja.

A Viète-formulák nem valami titkós gyógyszer hatóanyag, hanem a másodfokú egyenlet gyökei és együtthatói közötti összefüggéseket írja le.

Egyenlőtlenségek

Hogyan kell megoldani egyenlőtlenségeket? Mi a különbség egyenletek és egyenlőtlenségek megoldási módszerei között? Egyenlőtlenségek megoldása számegyenesen előjel ábrázolással.

Az elsőfokú egyenlőtlenségeknél még izgalmasabbak a másodfokú egyenlőtlenségek.

Síkgeometria

Hogyan számítjuk egyenes és sík távolságát?

Hogyan számíthatjuk ki két egyenes távolságát?

Két pont távolsága a pontokat összekötő szakasz hossza.

Hogyan számíthatjuk ki két sík távolságát?

Két ponttól azonos távolságra lévő pontok halmaza. Három ponttól azonos távolságra lévő pontok halmaza. Két metsző egyenestől azonos távolságra lévő pontok halmaza.

Hogyan számíthatjuk ki pont és egyenes távolságát?

Hogyan számíthatjuk ki pont és sík távolságát?

Pont, egyenes és sík a tér elemei, alapfogalmak, nem definiáljuk őket, hanem a szemléletből kialakult jelentésükre hagyatkozunk.

A háromszög köré írható körének középpontja az oldalfelezőmerőlegesei metszéspontja. Hogyan lehet megszerkeszteni egy háromszög köré írható körét

A magasságvonal a háromszög egy csúcsából a szemközti oldal egyenesére bocsátott merőleges. A magasságvonalak metszéspontja a magasságpont.

A háromszög súlyvonala a csúcsot a szemközti oldal felezőpontjával összekötő szakasz. Ezek metszéspontja a súlypont.

A háromszög belső szögfelezőinek metszéspontja a háromszög köré írható körének középpontja.

Néhány képlet háromszögek területére.

Azok a háromszögek, amelyeknek van 90°-os szöge.

Az egyenlőszárú háromszögben van két egyforma hosszú oldal.

Szabályos háromszögnek minden oldala és minden szöge egyenlő (tehát a szögek 60°-osak).

Azokat a négyszögeket nevezzük deltoidnak, amik papírsárkány alakúak és az átlóik merőlegesek egymásra.

A legszabályosabb négyszög a négyzet.

A paralelogramma olyan négyszög, aminek van két párhuzamos oldalpárja.

Rombusznál az oldalak egyenlő hosszúságúak, de a szögeknek nem kell derékszögnek lenniük.

Téglalapnál a szögek derékszögek, de az oldalak nem feltétlen egyenlő hosszúak.

A trapéz olyan négyszög, aminek van legalább egy párhuzamos oldalpárja.

A derékszögű háromszögben a befogók négyzetének összege egyenlő az átfogó négyzetével.

Ha egy kör átmérőjét összekötjük a körvonal egy másik, tetszőleges C pontjával, akkor a C csúcsnál derékszöget kapunk.

A húrnégyszög egy olyan négyszög, amelynek minden oldala ugyanannak a körnek egy-egy húrja.

A kerületi szög egy körben lévő szög úgy, hogy a szög csúcsa a körvonal egy pontja, szárai pedig vagy a kör két húrja, vagy egy húrja és egy érintője.

Egy kör adott ívéhez tartozó kerületi szögek mind ugyanakkorák.

Egy körben egy adott ívhez tartozó bármely középponti szög nagysága kétszerese az ugyanazon ívhez tartozó kerületi szög nagyságának.

Két szimmetrikus körív, amely megadja azokat a pontokat, amik alatt egy szakasz azonos szögben látható.

Kör kerületének és területének képletei.

Mi az a körcikk, és hogyan számolható ki az ívhossza és területe.

Egybevágósági transzformációk

A tengelyes tükrözés során egy egyenesre tükrözünk, amit tengelynek nevezünk.

Egy alakzatot vagy sokszögek tengelyesen szimmetrikusnak nevezünk, ha van olyan tengelyes tükrözés, aminek a hatására a tükörképe önmaga.

Hogyan kell megszerkeszteni egy alakzat középpontosan tükrözött képét, és mik a középpontos tükrözés tulajdonságai.

Egy alakzat vagy sokszög akkor középpontosan szimmetrikus, ha van olyan középpontos tükrözés, aminek hatására a tükörképe önmaga lesz.

Egy alakzatot vagy sokszöget forgás-szimmetrikusnak nevezünk, hogyha van olyan O pont, ami körül egy 0 és 360 fok közé eső szöggel elforgatva a sokszöget önmagába tudjuk forgatni.

A pont körüli forgatáshoz kell egy pont, ami körül forgatunk, na és persze egy szög.

Az eltolás során az alakzat lényegében ugyanaz marad, csak kicsit arrébb kerül.

Két alakzat akkor egybevágó, ha van olyan egybevágósági transzformáció, ami az egyiket a másikba viszi.

Háromszögek egybevágóságának 4 esete.

Abszolútértékes egyenletek és egyenlőtlenségek

Egy szám abszolútértékén a nullától való távolságát értjük.

Egyenletrendszerek

A behelyettesítő módszer az egyenletrendszerek megoldásának egyik technikája, ami során az egyik ismeretlent kifejezzük a másikkal.

Az egyenlő együtthatók módszere egy megoldási technika az egyenletrendszerekhez, ami során a két egyenletet összeadjuk vagy kivonjuk egymásból.

Gyökös azonosságok és gyökös egyenletek

Gyökös kifejezések szorzása és osztása közti összefüggések.

Egy a szám köbgyöke az a szám, aminek a köbe a.

Köbgyökös kifejezések szorzása és osztása közti összefüggések.

A gyökvonás másképpp viselkedik páros, illetve páratlan gyökkitevő esetén, így kétféle definíciónk lesz.

Egy a nem negatív szám négyzetgyöke az a nem negatív szám, aminek a négyzete a.

Megnézzük, hogy milyen izgalmak fordulhatnak elő a gyökös egyenletek világában. Hogyan kell megoldani egy gyökös egyenletet? Mikor lehet egy egyenletet négyzetre emelni? Milyen kikötéseket kell tenni egy gyökös egyenlet megoldásánál? Törtes gyökös egyenletek. Másodfokú egyenletre vezető gyökös egyenletek.

Szöveges feladatok

Utazásról szóló szöveges feladatok.

Középpontos hasonlóság

A középpontos hasonlósági transzformációhoz adott egy O pont, ez a középpont, és egy lambda nem nulla valós szám, ez a hasonlóság aránya.

Ha egy szög szárait párhuzamos egyenesekkel metsszük, akkor az egyik szögszáron keletkező szakaszok aránya megegyezik a másik szögszáron keletkező megfelelő szakaszok arányával.

Háromszögek hasonlóságának 4 esete.

Derékszögű háromszög egy befogója mértani közepe az átfogónak és a befogóra eső vetületének.

Derékszögű háromszögben az átfogó magasságának talppontja az átfogót két olyan részre bontja, melyeknek a mértani közepe a magasság:

Hasonló alakzatok területe négyzetesen, térfogata köbösen aránylik egymáshoz.

Bármely háromszögben egy csúcshoz tartozó belső szögfelező a szöggel szemközti oldalt a szomszédos oldalak arányában fogja kettéosztani.

Trigonometria

Mi az egység sugarú kör? Mi az a szinusz és koszinusz? Mire jó a szinusz és a koszinusz? Mi az a radián? Mi a kapcsolat a fok és a radián között?

Megnézzük, hogy derékszögű háromszögekben mit jelent a koszinusz. Mire jó a a koszinusz, mire lehet használni? Geometriai feladatok megoldása koszinusz szögfüggvény segítségével.

Megnézzük, hogy derékszögű háromszögekben mit jelent a szinusz. Mire jó a szinusz, mire lehet használni? Geometriai feladatok megoldása szinusz szögfüggvény segítségével.

Derékszögű háromszögben a szinusz a szöggel szemközti befogó és átfogó hányadosa. A koszinusz a szög melleti befogó és átfogó hányadosa. A tangens a szöggel szemközti befogó és szög melletti befogó hányadosa.

Derékszögű háromszögben egy szög tangense a szöggel szemközti befogó és szög melletti befogó hányadosa.

A háromszög területe kiszámítható a két oldal és a közrefogott szög szinuszának szorzataként, osztva 2-vel.

Ha a kört kettéosztjuk egy húrjával, akkor körszeleteket kapunk. A körszelet területe az őt magába foglaló körcikk és egyenlőszárú háromszög különbsége.

Kombinatorika

$n$ faktoriálisán az $n$-nél kisebb vagy egyenlő pozitív egész számok szorzatát értjük.

Egy adott n elemű halmaz elemeinek egy ismétlés nélküli permutációján az n különböző elem egy sorba rendezését értjük.

Ismétlés nélküli variációról akkor beszélünk, ha n különböző elem közül kiválasztunk k db.-ot úgy, hogy a kiválasztott elemek sorrendje is számít.

Ismétlés nélküli kombinációról akkor beszélünk, ha n különböző elem közül kiválasztunk k db.-ot úgy, hogy a kiválasztott elemek sorrendjére nem vagyunk tekintettel.

Ismétléses permutációról akkor beszélünk, ha n elem sorrendjére vagyunk kiváncsiak, de ezen elemek között vannak megegyezőek is.

Ismétléses variációról akkor beszélünk, ha n különböző elem közül kiválasztunk k db.-ot úgy, hogy a kiválasztott elemek sorrendje is számít és egy elemet többször is választhatunk.

Ha kör alakban helyezünk el n különböző elemet és azok sorrendjét vizsgáljuk, akkor ciklikus permutációról beszélünk.

Exponenciális egyenletek és egyenlőtlenségek

Az exponenciális függvények meglehetősen fontosak a matematikában, sőt nem csak a matematikában. Itt jönnek az exponenciális függvények.

Készítünk egy szuper-érthető összefoglalót a hatványazonosságokból. Megnézzük, hogyan kell a hatványazonosságokat használni. Megnézzük mi az az exponenciális függvény és hogyan kell ábrázolni.

Mik azok az exponenciális egyenletek? Hogyan kell megoldani egy exponenciális egyenletet? Törtes exponenciális egyenletek. Másodfokú egyenletre vezető exponenciális egyenletek.

Mik azok az exponenciális egyenlőtlenségek? Hogyan kell megoldani egy exponenciális egyenlőtlenséget?

Logaritmus, logaritmusos egyenletek, egyenlőtlenségek

Itt végre szuper-érthetően kiderül, hogy mi az a logaritmus. Készítünk egy gyors kis összefoglalót a logaritmus azonosságairól. Megnézzük, hogyan kell a logaritmus azonosságokat használni. Megnézzük mi az a logaritmus függvény és hogyan kell ábrázolni.

Készítünk egy szuper-érthető összefoglalót a logaritmus azonosságokról. Megnézzük, hogyan kell az azonosságokat használni, milyen kikötéseket kell tenni a logaritmikus kifejezéseknél, hogyan néz ki a logaritmus függvény.

Mik azok a logaritmusos egyenletek? Hogyan kell megoldani egy logaritmikus egyenletet? Milyen kikötéseket kell tenni egy logaritmusos egyenlet megoldásánál? Törtes logaritmikus egyenletek. Másodfokú egyenletre vezető logaritmikus egyenletek.

Trigonometrikus egyenletek és egyenlőtlenségek

Mi az egység sugarú kör? Mi az a szinusz és koszinusz? Mire jó a szinusz és a koszinusz? Mi az a radián? Mi a kapcsolat a fok és a radián között?

Az egységkör egy szöggel elforgatott egységvektorának végpontjának x koordinátáját nevezzük a szög koszinuszának

Az egységkör egy szöggel elforgatott egységvektorának végpontjának y koordinátáját nevezzük a szög szinuszának.

Egy szög tangense a szög szinuszának és koszinuszának hányadosával egyenlő.

Trigonometriai képlet összefoglaló. Összefüggések a tangens és kotangens között. A trigonometria alapegyenlete. Szögek kétszeresének szinusza és koszinusza.

Szinuszt és koszinuszt tartalmazó egyenletek megoldásának lépései.

Trigonometrikus függvényeknek vagy szögfüggvényeknek nevezzük azokat a függvényeket, amelyek tartalmaznak trigonometrikus kifejezéseket, mint például szinusz, koszinusz vagy tangens. Ezek eredetileg egy derékszögű háromszög egy szöge és két oldala hányadosa közti összefüggéseket írja le.

Szinusztétel és koszinusztétel

A Szinusz tétel szerint tetszőleges háromszögben bármely oldalak aránya megegyezik a velük szemközti szögek szinuszának arányával.

A Koszinusz tétel szerint tetszőleges háromszögben egy tetszőleges oldal négyzete egyenlő a másik két oldal négyzetének összege és a másik két oldal illetve a kiválasztott oldallal szemközti szög koszinuszának szorzatának különbségével.

Feladatok függvényekkel

A másodfokú függvény olyan függvény, amelynek legmagasabb fokú tagja másodfokú.

Trigonometrikus függvényeknek vagy szögfüggvényeknek nevezzük azokat a függvényeket, amelyek tartalmaznak trigonometrikus kifejezéseket, mint például szinusz, koszinusz vagy tangens. Ezek eredetileg egy derékszögű háromszög egy szöge és két oldala hányadosa közti összefüggéseket írja le.

Vektorok

A vektor egy irányított szakasz.

Két pont közti vektor a végpontba mutató helyvektor minusz a kezdőpontba mutató helyvektor.

Egy vektor hosszát megkapjuk, ha vesszük a koordinátái négyzetösszegének a gyökét. Két pont távolsága az őket összekötő vektor hossza.

Vektorok összeadásakor összeadjuk az x koordinátákat és összeadjuk az y koordinátákat. Kivonáskor vesszük az x koordináták különbségét és az y koordináták különbségét.

Koordinátageometria

Mi az normálvektor? Mi az irányvektor? Egyenes egyenletének felírása, pont és egyenes távolsága, párhuzamos és merőleges egyenesek.

Az irányvektor az egyenessel párhuzamos nem nullvektor.

A normálvektor az egyenesre merőleges nem nullvektor.

Egyenes egyenletének felírása, pont és egyenes távolságának kiszámolása, képlet pont és egyenes távolságára.

Hogyan írjuk föl egy kör egyenletét? A kör kanonikus egyenlete, a kör középpontja és sugara, kör és egyenes metszéspontja.

A parabola (emelt szint)

A parabola azon pontok halmaza a síkon, amelyek egy v egyenestől (vezéregyenes) és az egyenesre nem illeszkedő F ponttól (fókuszpont) egyenlő távolságra vannak.

Hogyan írhatjuk fel a parabola egyenletét és milyen adatokra van ehhez szükség.

A parabola egyenlete, ha tengelye párhuzamos az x tengellyel, illetve ha tengelye párhuzamos az y tengellyel.

A teljes indukció (emelt szint)

A teljes indukció egy bizonyítási módszer, ami olyan állítások bizonyítására alkalmas, melyek n pozitív egész számtól függenek.

Számtani és mértani sorozatok

Megnézzük a számtani sorozat általános tagjának képletét, valamint a számtani sorozat összegképletét.

Itt jön a mértani sorozat általános tagjának kélete és a mértani sorozat összegképlete.

Százalékszámítás és pénzügyi számítások

Hogyan írjuk fel, ha egy értéket x %-al növeltünk, vagy csökkentettünk.

A kamatos kamat számításának képlete.

Térgeometria

A kúp egy gúlaszerű térbeli test, melynek alapja egy kör.

Megnézzük, hogy mi a kúp és a henger, mit jelent a palást és az is kiderül, hogy hogyan kell kiszámolni a kúpok és hengerek térfogatát és felszínét. Aztán nézünk néhány feladatot hengerekre és kúpokra.

Megnézzük, hogy mi a kúp és a henger, mit jelent a palást és az is kiderül, hogy hogyan kell kiszámolni a kúpok és hengerek térfogatát és felszínét. Aztán nézünk néhány feladatot hengerekre és kúpokra.

Itt térgeometriai izgalmak kezdődnek. Megnézzük, hogy mi a gúla és mi a hasáb, mit jelent a palást és az is kiderül, hogy hogyan kell kiszámolni a gúlák és hasábok térfogatát és felszínét. Aztán nézünk néhány feladatot gúlákra és hasábokra, hengerekre és kúpokra. Megnézzük azt is, hogy egy test méreteinek változtatásával a felszíne négyzetesen, a térfogata pedig köbösen változik.

Nézzük, hogyan kell kiszámolni a gúlák felszínét.

Lássuk, hogyan kell kiszámolni a gúlák térfogatát.

Itt térgeometriai izgalmak kezdődnek. Megnézzük, hogy mi a gúla és mi a hasáb, mit jelent a palást és az is kiderül, hogy hogyan kell kiszámolni a gúlák és hasábok térfogatát és felszínét. Aztán nézünk néhány feladatot gúlákra és hasábokra, hengerekre és kúpokra. Megnézzük azt is, hogy egy test méreteinek változtatásával a felszíne négyzetesen, a térfogata pedig köbösen változik.

Na és itt jön a hasábok felszíne.

Lássuk, hogyan kell kiszámolni a hasábok térfogatát.

A henger olyan, mint a hasáb, csak nem sokszög a két párhuzamos lap, hanem kör.

Képlet henger felszínére.

Képlet henger térfogatára.

Ha a gömböt kettévágjuk egy olyan síkkal, ami épp átmegy a középpontján, akkor a vágás során keletkező kör sugara éppen megegyezik a gömb sugarával. Ezt a kört nevezzük főkörnek.

A gömb egy adott ponttól (középpont) egyenlő távolságra lévő pontok halmaza.

Ha a gömb középpontját összekötjük a gömbfelület bármelyik pontjával, akkor az így keletkező szakasz hossza állandó, és ez az állandó hosszúság a gömb sugara. Ha meghosszabbítjuk ezt a szakaszt a másik irányba is, akkor egy átmérőt kapunk

Képlet a gömb felszínére.

Ha a gömb középpontját összekötjük a gömbfelület bármelyik pontjával, akkor az így keletkező szakasz hossza állandó, és ez az állandó hosszúság a gömb sugara.

Képlet a gömb térfogatára.

Ha egy gúlát az alaplap síkjával párhuzamosan metszünk el, akkor egy csonkagúlát kapunk.

Képlet a csonkagúla felszínének kiszámítására.

Képlet a csonkagúla térfogatának kiszámítására.

Ha egy forgáskúpot az alaplap síkjával párhuzamosan metszünk el, akkor egy csonkakúpot kapunk.

Képlet a csonkakúp felszínének kiszámítására.

Képlet a csonkakúp térfogatának kiszámítására.

Valószínűségszámítás

Eseményeknek nevezzük a valószínűségi kísérlet során bekövetkező lehetséges kimeneteleket.

A valószínűség kiszámításának klasszikus modellje az, hogy megszámoljuk hány elemi eseményből áll a vizsgált esemény és ezt elosztjuk az összes elemi esemény számával.

Ha a szövegben valószínűségek vannak megadva, akkor a binomiális eloszlást szoktuk használni.

A hipergeometriai eloszlás a visszatevés nélküli mintavételhez kapcsolódó eloszlás.

Ha húzásokat vizsgálunk úgy, hogy a kihúzott elemeket nem tesszük vissza, akkor ez egy visszatevés nélküli mintavétel.

A visszatevées mintavételhez kapcsolódó eloszlás a binomiális eloszlás.

Mikor mondjuk, hogy két esemény egymástól független? Példák független eseményekre.

Mikor kizáró két esemény? Példák kizáró eseményekre.

A várható érték

A valószínűségekkel súlyozott átlag.

Statisztika

A medián a növekvő sorba rendezett adatsor középső értéke.

A módusz a leggyakoribb érték.

Az átlag az összes elem összege osztva az elemszámmal.

Az átlagtól való átlagos eltérést szórásnak nevezzük és egy szigma nevű görög betűvel jelöljük.

Az adatsor első felének a felezőpontja az alsó kvartilis.

A kvartilisek és a medián azt szemlélteti, hogyan oszlanak el az adatsorban szereplő adatok.

Az adatsor második felének a felezőpontja a felső kvartilis.

A relatív szórás azt mondja meg, hogy a szórás az átlagnak hány százaléka:

Sorozatok határértéke (emelt szint)

Nevezetes 0-hoz tartó sorozatok.

Nevezetes végtelenhez tartó sorozatok.

Nevezetes gyökös sorozatok határértéke.

Exponenciális kifejezések határértéke.

Ha egy sorozat határértéke valós szám, akkor a sorozatot konvergensnek nevezzük. Ha a sorozat határértéke plusz vagy mínusz végtelen, illetve ha egyáltalán nincs is határértéke, akkor a sorozatot divergensnek nevezzük. Az ugráló sorozatokat oszcillálónak nevezzük. Lássunk néhány példát.

Sorozatok monotonitása és korlátossága (emelt szint)

Ha egy sorozat határértéke valós szám, akkor a sorozatot konvergensnek nevezzük.

A sorozatok egyik legfontosabb tulajdonsága a határértékük, ami azt jelenti, hogy mi történik a sorozattal ahogy egyre és egyre nagyobb indexű tagjait vizsgáljuk.

Ha a sorozat határértéke plusz vagy mínusz végtelen, illetve ha egyáltalán nincs is határértéke, akkor a sorozatot divergensnek nevezzük.

A sorozat monotonitása lehet monton nő, monoton csökkenő, szigorúan monoton nő, szigorúan monoton csökkenő.

Függvények határértéke és folytonossága (emelt szint)

Egy függvényt akkor nevezünk folytonosnak valamely pontban, ha itt a függvényérték és a határérték megegyezik. Lássuk miért is ennyire fontos ez.

Beszéljünk egy kicsit a trigonometrikus függvények határértékéről. Néhány nevezetes határérték, élükön a sinx/x típusúval.

Deriválás (emelt szint)

Függvény konstansszorosának, két függvény összegének, szorzatának és hányadosának deriválási szabályai. Összetett függvények deriválási szabálya.

Egy szelő egyenes meredeksége a differenciahányados.

Egy függvény érintő egyenesének meredeksége a differenciálhányados.

Konstans deriváltja, polinomok deriválási szabálya. Az exponenciális és logaritmus függvények deriválása. Trigonometrikus függvények deriváltjai.

Függvények érintője (emelt szint)

A függvény érintője egy olyan egyenes, amely egy függvényt pontosan egy pontban érint.

Az integrálás (emelt szint)

Az f(x) függvény primitív függvényének jele F(x) és azt tudja, hogy ha deriváljuk, akkor visszakapjuk f(x)-et. Egy függvény primitív függvényeinek halmazát nevezzük a függvény határozatlan integráljának.

Polinomok integrálása. Törtfüggvény integrálása. Exponenciális függvények integrálása. Trigonometrikus függvények integrálása.

Polinomok, törtfüggvény, exponenciális függvények, trigonometrikus függvények integráljainak lineáris helyettesítései.

A Newton-Leibniz formula egy egyszerűen használható képlet a határozott integrál kiszámításához. Ez a tétel az egész matematika történetének egyik legfontosabb tétele. Egy Newton nevű angol fizikus és egy Leibniz nevű német filozófus egyszerre találta ki az 1600-as évek végén.