Egyenletek megoldása logaritmussal
>+4^=\dfrac\;” />
Logaritmus megoldások
Oldjuk meg a következő logaritmusos egyenletet:
lg(x- 6) + lg(2x – 14) = 3 – lg 25.
Megoldás: alkalmazzuk az azonosságokat
Az egyenletalaphalmaza a 7-nél nagyobb valós számok halmaza (x – 6 > 0 és 2x – 14 > 0). A 3-at ajánlatos lg 1000-nek tekintenünk. Ezután a logaritmusazonosságai alapján:
Azonos alapú logaritmusértékekegyenlőségéből következik a számok egyenlősége:
Elvégezzük a beszorzást, összevonást, majd rendezzük az egyenletet:
2-vel oszthatunk is. A másodfokú egyenletnek a gyökei:
A 2 nem eleme az egyenletalaphalmazának, ezért az eredeti egyenletnek a gyöke:
Számolásaink helyességét behelyettesítéssel ellenőrizhetjük, az x = 11 valóban gyöke az eredeti egyenletnek.
Egyenletek megoldása logaritmussal
Ehhez a tanegységhez ismerned kell a hatványozás azonosságait, a logaritmus azonosságait és a mérlegelvet.
Tanulási célok
Ebből a tanegységből megtanulod azokat a „fogásokat”, amelyeket a logaritmus segítségével megoldható egyenleteknél alkalmazhatsz.
Narráció szövege
Több olyan problémával is találkozhattál már, amiknek a megoldásában a logaritmus segített. Ilyenek lehettek az exponenciális vagy logaritmusos jelenségekkel, folyamatokkal kapcsolatos kérdések, feladatok is.
A következőkben áttekintünk néhány típusfeladatot és azok megoldásait.
Először olyan exponenciális egyenlet megoldásáról lesz szó, amiben a logaritmusra is szükség van.
Oldjuk meg $3 \cdot > = 15$ egyenletet a valós számok halmazán! Először célszerű mindkét oldalt 3-mal osztani.
A következő lépésben használhatjuk a kettes alapú logaritmus definícióját, de más gondolatmenetet is. Az első módszert már többször alkalmaztuk, most nézzük a másikat!
Ha két pozitív szám egyenlő, akkor egyenlő a tízes alapú logaritmusuk is.
Az egyenlet bal oldalát a hatvány logaritmusára vonatkozó azonosság alapján más alakban is írhatjuk. Ez egy elsőfokú egyismeretlenes egyenlet, ennek megfelelően a mérlegelvvel folytathatjuk a megoldást. Az egyenlet gyöke közelítőleg 1,83. A megoldást ellenőrizhetjük behelyettesítéssel is. Nem 15-öt kapunk a bal oldalon, ennek az az oka, hogy a megoldás során kerekítést is alkalmaztunk.
Második példánkban a logaritmus azonosságait kell segítségül hívnunk. Oldjuk meg a pozitív valós számok halmazán a $\lg x + \lg \left( \right) = 1$ egyenletet!
Az egyenlet bal oldalán két azonos alapú logaritmus összege áll. Erre alkalmazhatjuk a tanult azonosságot. Tehát egy számnak a tízes alapú logaritmusa 1-gyel egyenlő. Ilyen szám csak egy van, a 10.
A zárójel felbontása után kiderül, hogy egy másodfokú egyenlethez jutottunk. Ezt megoldóképlettel oldjuk meg. Két gyököt kapunk. Közülük a negatív nem lehetséges, hiszen a pozitív számok halmazán kerestük a megoldást. Tehát csak a 2 lehet megoldása az eredeti egyenletnek, ezt behelyettesítéssel ellenőrizhetjük.
Harmadik példaként egy bonyolultnak látszó egyenletet oldunk meg.
Mielőtt nekilátnánk a megoldásnak, máris elmondhatjuk, hogy csak a pozitív számok között érdemes megoldást keresnünk. Ennek az az oka, hogy csak pozitív számoknak van logaritmusuk, és az egyenlet bal oldalán álló első tag éppen az x logaritmusával egyenlő.
Kétféleképpen is elindulhatunk. Mindkét megoldás a logaritmus azonosságait használja.
Lássuk az első indítását és a további lépéseket is! A szorzat logaritmusára vonatkozó azonosságot alkalmazzuk az egyenlet bal oldalán álló első három tagra. Használjuk az azonos alapú hatványok szorzására vonatkozó azonosságot, majd a hányados logaritmusára vonatkozó azonosságot alkalmazzuk.
A kettes alapú logaritmusfüggvény szigorúan monoton, ezért az egyenlőség pontosan akkor lehetséges, ha $ = 64$.
Egy pozitív és egy negatív gyököt kapunk, de az eredeti egyenletnek csak pozitív szám, vagyis a 8 lehet a megoldása. Behelyettesítéssel ezt is ellenőrizhetjük.
A másik megoldás indításában a hatvány logaritmusára vonatkozó azonosságot alkalmazzuk a második, harmadik és negyedik tagra.
A bal oldalon összesen 2-szer áll, a jobb oldalon pedig 6, mert $64 = $.
A logaritmus definícióját alkalmazva ismét a 8-at kapjuk megoldásként.
A harmadik példa mindkét megoldása jó, nincs olyan szempont, amelyik szerint az egyiket vagy a másikat lenne célszerűbb választani. Mindkét megoldás gyorsan és biztonságosan célhoz vezet, ha kellően körültekintő vagy.
A bemutatott példákon kívül még számos könnyebben és nehezebben megoldható exponenciális vagy logaritmusos egyenlettel találkozhatsz. A hatványozás azonosságai, a logaritmus definíciója és a logaritmus azonosságai a legtöbb esetben téged is elvezetnek a sikeres megoldáshoz.
Érettségi gyakorló 1./Megoldások
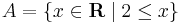
és a
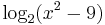
x 2 − 9 képe egy fölfelé nyitott parabola, gyökökkel, ezért ez a kifejezés x < − 3 ill. 3 < x esetekben pozitív:
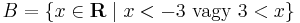
+8\cdot a-1=0\;” /> =\dfrac<-8\pm\sqrt<64-4\cdot 9\cdot (-1) >>=\dfrac<-8\pm 10>=\qquad \dfrac,\qquad -1″ />
Innen az új ismeretlent definiáló egynletbe visszahelyettesítve, egyfelől:
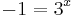
ami lehetetlen, továbbá:
=3^x\,” /> =3^x\,” />
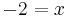
Exponenciális egyenlet gyakorló
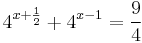
Logaritmikus egyenlet

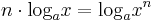
(ahol x > 0 , a > 0 , a≠1). Tehát:
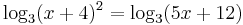
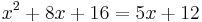
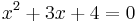
aminek a gyökei a másodfokú egyenlet megoldóképlete alapján:
A -1 megoldás, mert behelyettesítve az eredeti egyenletbe:
_3(-1+4)=2\cdot\mathrm_3 3 =2\;” /> _3(-5+12)=\mathrm_3 9=2\,” />
De a -3 nem megoldás, mert ekkor a jobb oldal nincs értelmezve
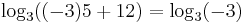
| vissza |
Logaritmikus egyenlet gyakorló
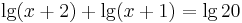
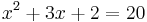
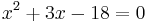
aminek a gyökei a másodfokú egyenlet megoldóképlete alapján:
amelyek közül a -6 nem felel meg az x > − 1 kikötésnek, de a 3 megoldás, mert:
Logaritmus, logaritmikus egyenletek
Válaszd ki, hogy melyik év középszintű érettségi feladataival szeretnél gyakorolni.
2020 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
ELSŐ RÉSZ


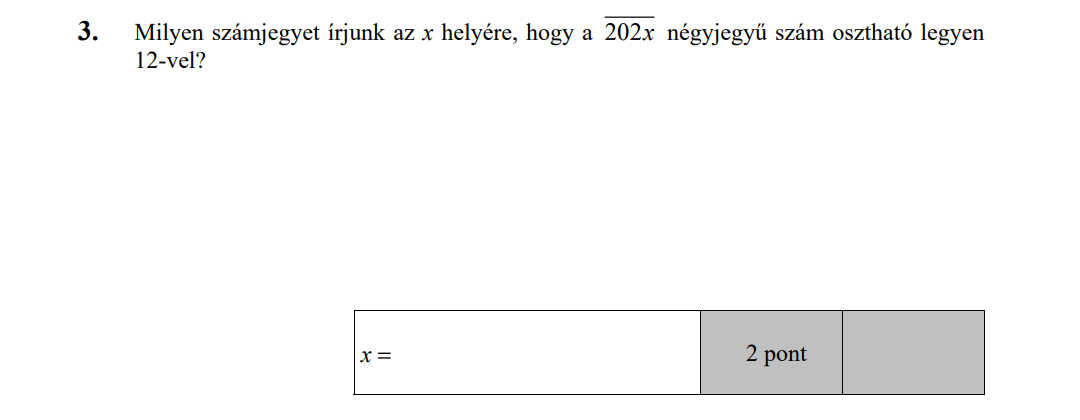
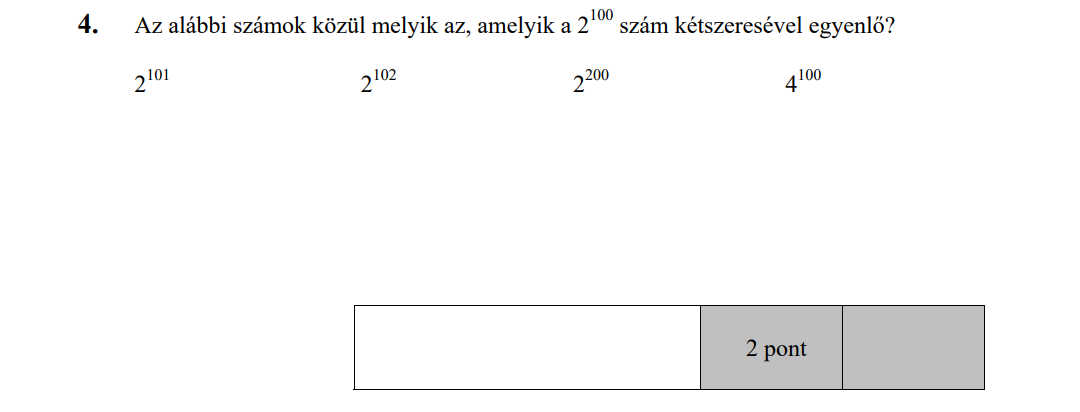







MÁSODIK RÉSZ






2020 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
ELSŐ RÉSZ


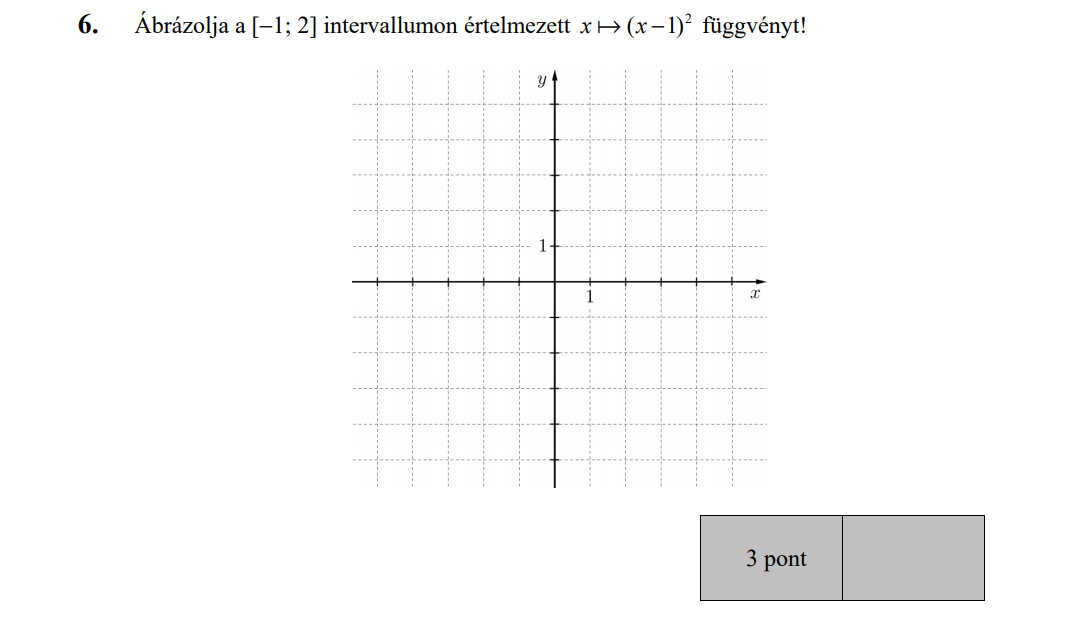



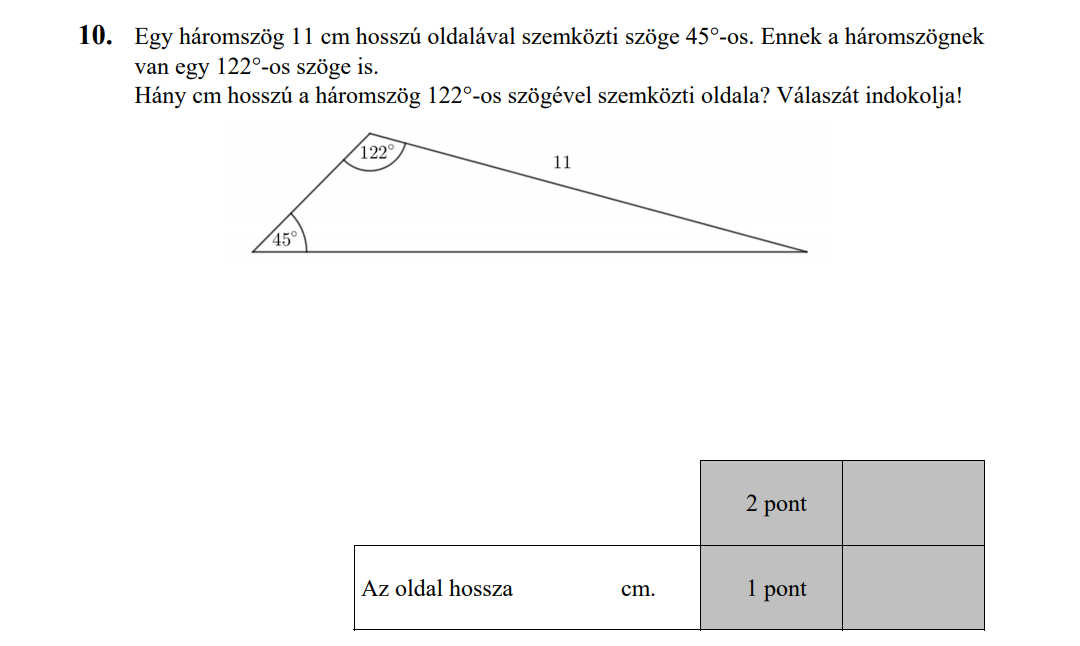
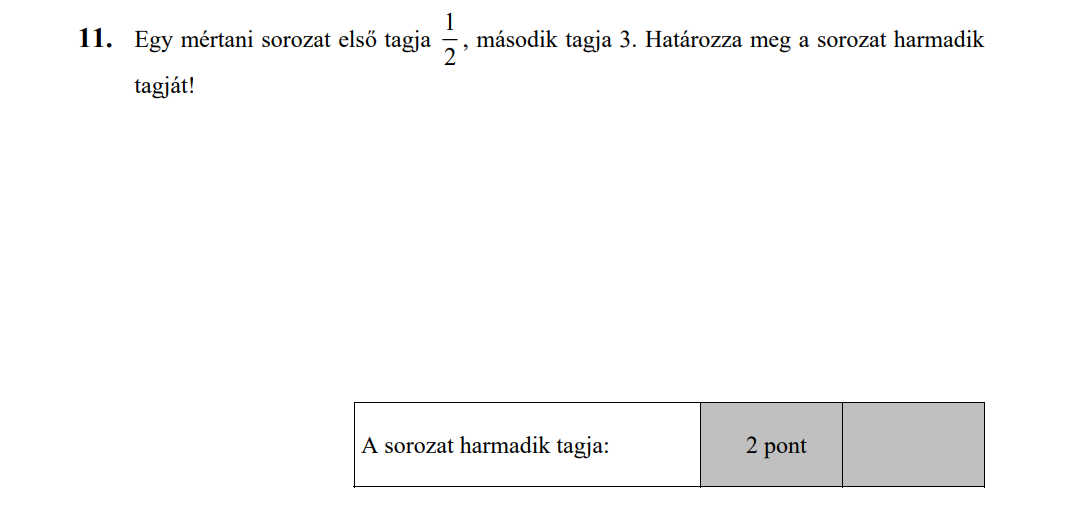

MÁSODIK RÉSZ

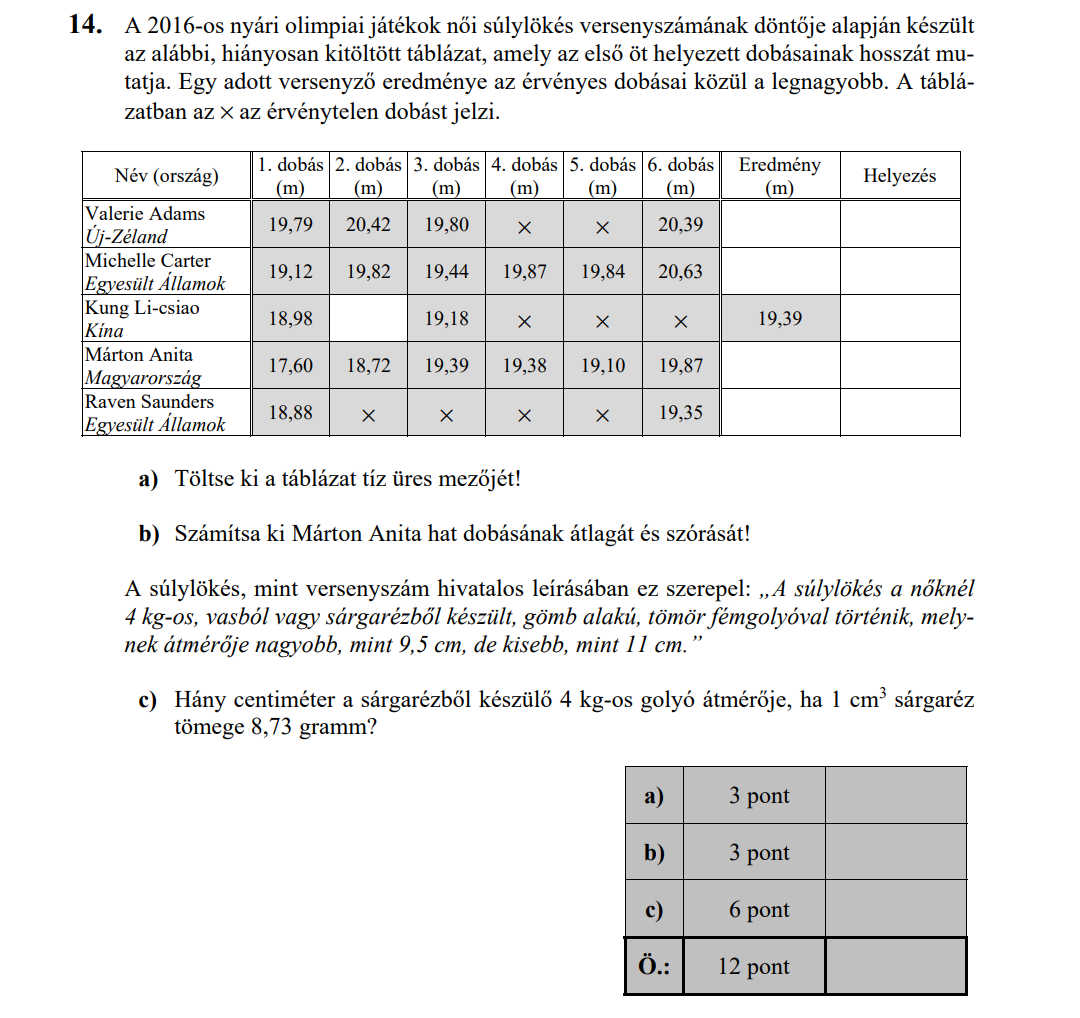




2019 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
ELSŐ RÉSZ
MÁSODIK RÉSZ
2019 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
ELSŐ RÉSZ
MÁSODIK RÉSZ
2018 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
ELSŐ RÉSZ
MÁSODIK RÉSZ
2018 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
ELSŐ RÉSZ
MÁSODIK RÉSZ
2017 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
ELSŐ RÉSZ
MÁSODIK RÉSZ
2017 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
ELSŐ RÉSZ
MÁSODIK RÉSZ
2016 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
ELSŐ RÉSZ
MÁSODIK RÉSZ
2016 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
ELSŐ RÉSZ
MÁSODIK RÉSZ
2015 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
ELSŐ RÉSZ
MÁSODIK RÉSZ
2015 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
ELSŐ RÉSZ
MÁSODIK RÉSZ
2014 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
ELSŐ RÉSZ
MÁSODIK RÉSZ
2014 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
ELSŐ RÉSZ
MÁSODIK RÉSZ
2013 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
ELSŐ RÉSZ
MÁSODIK RÉSZ
2013 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
ELSŐ RÉSZ
MÁSODIK RÉSZ
2012 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
ELSŐ RÉSZ
MÁSODIK RÉSZ
Logaritmus
Logaritmus azonosságok
Logaritmikus egyenlet megoldása
A logaritmikus egyenletek megoldásának lényege, hogy ilyen alakra jussunk:
Mert innen a logaritmus definíciója miatt az következik, hogy
Ahhoz, hogy a bonyolúltabb egyenleteket is ilyen alakra hozzuk, a logaritmus azonosságait használjuk.
e) \( 3^x = 7 \qquad x=? \)
f) \( 4^+5 = 13 \qquad x=? \)
a) Egy baktériumtenyészet generációs ideje 25 perc, ami azt jelenti, hogy ennyi idő alatt duplázódik meg a baktériumok száma a tenyészetben. Kezdetben 5 milligramm baktérium volt, hány perc múlva lesz a tenyészetben 30 milligramm baktérium?
b) Egy másik baktériumtenyészetben 40 perc alatt 3 szorosára nő a baktériumok száma. Mennyi a generációs idő, vagyis hány perc alatt duplázódik meg a baktériumok száma?
c) A radiaktív anyagok felezési ideje azt jelenti, hogy mennyi idő alatt csökken a radioaktív anyagban az atommagok száma a felére. A 239-plutónium felezési ideje például 24 ezer év, a 90-stonrciumé viszont csak 25 év.
Ez a remek kis képlet adja meg a radioaktív bomlás során az atommagok számát az idő függvényében:
Egy 90-stronciummal szennyezett területen hány százalékkal csökken 40 év alatt a radioaktív atommagok száma? Mennyi idő alatt csökken a 90%-ára a 90-stonrcium mennyisége?
A $T$ felezési idő 25 év, és az alábbi összefüggés áll fenn:
d) Egy anyagban a radioaktív atommagok száma 30 év alatt 12%-kal csökken. Mekkora a felezési idő? Mennyi idő alatt csökken 50%-ról 10%-ra az anyagban található radioaktív atomok száma?
Oldjuk meg az alábbi egyenleteket
d) \( \log_^2 – 7\cdot \log_ +12 = 0 \)
Oldjuk meg az alábbi egyenleteket
Oldjuk meg a következő logaritmusos egyenlőtlenségeket.
Oldjuk meg az alábbi egyenletet
\( x^2 \cdot \log_ – 3x^2 = 0 \)
Oldjuk meg az alábbi egyenletet
Oldjuk meg az alábbi egyenletet
Színre lép a logaritmus
És most egy új szereplő lép színre, a logaritmus.
Nos ez a logaritmus egy nagyon remek dolog, de kis magyarázatot igényel.
Mindössze arról van szó, hogy azt mondja meg, a-t hányadik hatványra kell emelni ahhoz, hogy x-et kapjunk.
Itt van például ez:
Ez azt jelenti, hogy 2-t hányadik hatványra kell emelnünk, hogy 8-at kapjunk.
Nos 23=8, tehát a válasz…
Vagy nézzük meg ezt:
Nos lássuk csak
Itt jön aztán egy nehezebb ügy:
A kérdés az, hogyan lesz a 8-ból 2. Az elosztjuk 4-gyel ugye nem jó válasz, mert valami hatványozás kell ide.
Próbáljuk meg kitalálni, mennyi lehet ez:
A kérdés, 8 a hányadikon a 16.
Nos ami a 8-ban és a 16-ban közös, az a 2, mert 23=8 és 24=16.
Így aztán úgy jutunk el a 8-ból a 16-hoz, hogy előbb a 8-ból csinálunk 2-t,
utána pedig a 2-ből 16-ot.
Mindezek után már nem jelenthet gondot ez sem:
Most pedig lássuk a logaritmusos azonosságokat.
A logaritmus egyik legnagyobb haszna az, hogy képesek vagyunk megoldani az ilyen egyenleteket, mint amilyen ez
Mindkét oldalnak vesszük a logaritmusát.
Általánosítva, ha van egy ilyen, hogy
akkor ebből így kapjuk meg x-et.
A megfordítását is jegyezzük meg, ha
akkor így kapjuk meg x-et.
Exponenciális egyenlet megoldása
Logaritmikus egyenlet megoldása
Oldjuk meg például ezeket:
Most pedig lássuk a függvényeket.
Egy baktériumtenyészet generációs ideje 25 perc, ami azt jelenti, hogy ennyi idő alatt duplázódik meg a baktériumok száma a tenyészetben. Kezdetben 5 milligramm baktérium volt a tenyészetben. Hány perc múlva lesz a tenyészetben 30 milligramm baktérium?
Készítsünk erről egy rajzot.
Azt, hogy éppen hány milligramm baktériumunk van, ezzel a kis képlettel kapjuk meg:
A történet végén 30 milligramm baktériumunk van.
Ezt az egyenletet kéne valahogy megoldanunk.
Ehhez az kell, hogy a 2x önállóan álljon. Ne legyen megszorozva senkivel.
Most jön a számológép, megnyomjuk rajta azokat a gombokat, hogy log, aztán 2 aztán 6.
Ha a világnak ahhoz a szerencsétlenebbik feléhez tartozunk, akiknek a számológépén csak sima log van…
Nos, akkor egy kis trükkre lesz szükség.
De így is kijön.
Itt az x=2,585 nem azt jelenti, hogy ennyi perc telt el…
Azt jelenti, hogy x=2,585 generációnyi idő telt el.
Egy másik baktériumtenyészetben 40 perc alatt 3 szorosára nő a baktériumok száma. Mennyi a generációs idő, vagyis hány perc alatt duplázódik meg a baktériumok száma?
Kezdetben van valamennyi baktérium.
aztán megint megduplázódik.
A mi történetünkben háromszorosára nő a baktériumok száma:
Megint jön a számológép és megnyomjuk rajta azokat a gombokat, hogy log, aztán 2 aztán 3.
Vagy ha az előbb így nem tudtuk kiszámolni, akkor feltehetően most se.
Ilyenkor segít nekünk ez a trükk.
És most nézzük, hogyan tovább.
Az x=1,585 azt jelenti, hogy ennyi generációs idő telt el 40 perc alatt.
Vagyis egy generációs idő hossza…
A baktériumok száma 25,24 perc alatt duplázódik meg.
A radioaktív anyagok felezési ideje azt jelenti, hogy mennyi idő alatt csökken a radioaktív anyagban az atommagok száma a felére. A 239-plutónium felezési ideje például 24 ezer év, a 90-stronciumé viszont csak 25 év.
Ez a remek kis képlet adja meg a radioaktív bomlás során az atommagok számát az idő függvényében:
Egy 90-stronciummal szennyezett területen hány százalékkal csökken 40 év alatt a radioaktív atommagok száma? Mennyi idő alatt csökken a 12,5%-ára a 90-stroncium mennyisége? A T felezési idő 25 év, és az alábbi összefüggés áll fenn:
Lássuk, mi történik 40 év alatt:
40 év alatt tehát a 33%-ára csökken a 90-stroncium atommagok száma.
Most nézzük, mennyi idő alatt csökken a 90%-ára az atommagok száma.
Tehát úgy néz ki, hogy 3,8 év alatt csökken 90%-ára az atommagok száma.
Egy anyagban a radioaktív atommagok száma 30 év alatt 12%-kal csökken. Mekkora a felezési idő? Mennyi idő alatt csökken 50%-ról 10%-ra az anyagban található radioaktív atomok száma?
Itt jön a mi kis képletünk:
30 év alatt 12%-kal csökkent:
Na, ez így sajna nem túl jó…
Ha valami 12%-kal csökken, akkor 88% lesz.
A felezési idő tehát 162,7 év.
Most nézzük, hogy mennyi idő alatt csökken 50%-ról 10%-ra a radioaktív atomok száma:
Comments are closed, but trackbacks and pingbacks are open.