Másodfokú függvény feladatok megoldással

MÉLYVÍZ A FÜGGVÉNYEK TENGERÉN.
Függvények grafikonjának ábrázolását gyakorolhatod az alábbi alkalmazással.
A függvényeket az alábbi képletek segítségével tudod megadni:

Másodfokú függvény feladatok megoldással

Másodfokú függvényekkel már foglalkoztunk. Tudjuk, hogy a legegyszerűbb másodfokú függvény a valós számok halmazán értelmezett függvény, képe a normálparabola. Láttuk, hogy függvénytranszformácikókkal ebből újabb másodfokú függvényeket állíthatunk elő.

A következőkben azt vizsgáljuk, hogy valamely másodfokú függvény hogyan állítható elő a legegyszerűbb másodfokú függvényből, hogyan kapható meg képe a normálparabolából. Vizsgálataink során olyan általános megállapításokat keresünk, amelyek segítségével bármely másodfokú függvény menetét pontosan jellemezhetjük (akár a képe megrajzolása nélkül).

Állapítsuk meg, hogy milyen transzformációkkal állítható elő az
függvényből a függvény, és jellemezzük a g függvényt!

Megoldás: másodfokú függvények transzformációja

Ehhez a g függvény hozzárendelési szabályát teljes négyzet alakban írjuk fel:
.
Ezért a g függvény:

Ebből az alakból leolvashatjuk az egymás utáni transzformációkat:
1.
2.
3.
Ezek a függvénytranszformációk a normálparabola geometriai transzformációit jelentik.

1. A normálparabolát 4 egységgel toljuk el.
2. Az eltolt normálparabola minden pontjának az y koordinátáját 2-vel szorozzuk, azaz a parabolát az y tengely irányába kétszeresére nyújtjuk.
3. A kapott parabolát 7 egységgel lefelé eltoljuk.

Az függvény a intervallumon monoton csökken, a intervallumon monoton nő, -nál csökkenésből növekedésbe megy át, ott minimuma van. A minimális függvényérték: .
Az f függvény képe az egyenletű parabola, tengelypontja a (0;0) pont, ez a parabola „legalsó” pontja.
A transzformációk folytán a függvény a intervallumon monoton csökken, a intervallumon monoton nő,
-nél csökkenésből növekedésbe megy át, ott minimuma van.
A minimális függvényérték: .
A g függvény képe az egyenletű parabola, tengelypontja a (4;-7) pont, ez a parabola „legalsó” pontja.
A g függvény zérushelyei a függvényhez kapcsolódó egyenlet gyökei:

A g függvény zérushelyei:

Tulajdonságok összefoglalása

A másodfokú függvényeknek azokat a tulajdonságait, amelyeket az előbbiekben megbeszéltünk, az alábbiakban összefoglaljuk: Az
, , ( )
másodfokú függvénynek vagy minimuma, vagy maximuma, közös néven szélsőértéke van.
Az előző f függvény hozzárendelési szabályát (teles négyzetté kiegészítéssel) átírtuk az alábbi alakba:
,
Ebből az alakból leolvashatjuk, hogy az f függvény képét a normálparabolából milyen geometriai transzformációkkal kapjuk meg.
Az , másodfokú függvény szélsőértékének x koordinátája:

A szélsőérték,
ha , akkor minimum,
ha , akkor maximum.
A szélsőértéknél a függvényérték:

Az , függvény zérushelyei az egyenlet gyökei.

Tudjuk, hogy a gyökök a diszkriminánstól függnek. A másodfokú függvények képe, a hozzájuk tartozó egyenletek diszkriminánsa és az egyenletek gyökei közötti kapcsolatot mutatja.

Feladatok függvényekhez

Függvények - feladatok és megoldások

2.) A következő függvények adottak, értelmezési tartományuk az !

f₁ : x → x + 1
f₂ : x → 2x
f₃ : x → x 2
f₄ : x →

MEGOLDÁS

$\begin{bmatrix}{x}&{-3}&{-2}&{-1}&{0}&{1}&{2}&{3}\\{f_1(x)}&{-2}&{-1}&{0}&{1}&{2}&{3}&{4}\end{bmatrix}$

MEGOLDÁS

$\begin{bmatrix}{x}&{-3}&{-2}&{-1}&{0}&{1}&{2}&{3}\\{f_2(x)}&{-6}&{-4}&{-2}&{0}&{2}&{4}&{6}\end{bmatrix}$

MEGOLDÁS

$\begin{bmatrix}{x}&{-3}&{-2}&{-1}&{0}&{1}&{2}&{3}\\{f_3(x)}&{9}&{4}&{1}&{0}&{1}&{4}&{9}\end{bmatrix}$

f₄ : x →

MEGOLDÁS

$\begin{bmatrix}{x}&{-3}&{-2}&{-1}&{0}&{1}&{2}&{3}\\{f_4(x)}&{-\frac{1}{3}}&{-\frac{1}{2}}&{-1}&{-}&{1}&{\frac{1}{2}}&{\frac{1}{3}}\end{bmatrix}$

a 0 x érték nem megengedett az osztás miatt

MEGOLDÁS

$f_1 : y = x + 1 \rightarrow f_1^{-1} : x = y + 1 \Rightarrow y = x - 1$

$f_2 : y = 2x \rightarrow f_2^{-1} : x = 2y \Rightarrow y = \frac{x}{2}$

$f_3 : y = x^2 \rightarrow f_3^{-1} : x = y^2 \Rightarrow y = \sqrt{x}$

$f_4 : y = \frac{1}{x} \rightarrow f_4^{-1} : x = \frac{1}{y} \Rightarrow y = \frac{1}{x}$

c.) Add össze az adott függvényeket!
Példa: f₁(x) + f₂(x) = x + 1 + 2x = 3x + 1

MEGOLDÁS

$f_2 + f_4 \Rightarrow 2x + \frac{1}{x} = \frac{2x^2 + 1}{x}$

MEGOLDÁS

$f_3 + f_4 \Rightarrow 2x + \frac{1}{x} = \frac{2x^2 + 1}{x}$

MEGOLDÁS

$f_1 * f_3 \Rightarrow x^2 * (x + 1) = x^3 + x^2$

MEGOLDÁS

Feladatok a lineáris függvényekhez

MEGOLDÁS

$x = -3y + 6 \Rightarrow y = \frac{x - 6}{3}$

MEGOLDÁS

$x = -\frac{3}{2}y + 9 \Rightarrow y = \frac{(x - 9) * 2}{3}$

MEGOLDÁS

$x = \frac{1}{3}y - 2 \Rightarrow y = (x + 2) * 3$

MEGOLDÁS

$-0,5x - 3 = x \Rightarrow x = -2,$

$x = -0,5y - 3 \Rightarrow y = -2(x + 3)$

MEGOLDÁS

$k = \frac{6 - 5}{4 - 3} = \frac{1}{1} = 1 \Rightarrow f(x) = x + 2$

MEGOLDÁS

$k = \frac{2 - 4}{2 - (-2)} = -\frac{2}{4} = -\frac{1}{2} \Rightarrow f(x) = -\frac{1}{2}x + 3$

MEGOLDÁS

$k = \frac{8 - 2}{6 - (-3)} = \frac{6}{9} = \frac{2}{3} \Rightarrow f(x) = \frac{2}{3}x + 4$

MEGOLDÁS

$k = \frac{-7,5 - (-1,5)}{3 - (-1)} = -\frac{6}{4} = -\frac{3}{2} \Rightarrow f(x) = -\frac{3}{2}x - 3$

MEGOLDÁS

$k = \frac{-3 - 2}{-1 - 1)} = \frac{-5}{-2} = \frac{5}{2} \Rightarrow f(x) = \frac{5}{2}x - 0,5$

MEGOLDÁS

$k = \frac{2,3 - 1,8}{8 - 3} = \frac{0,5}{5} = \frac{1}{10} \Rightarrow f(x) = \frac{1}{10}x + 1,5$

MEGOLDÁS

Értékkártya: w(x) = 0,6x
Tarifa A: a(x) = 0,2x + 10
Tarifa B: b(x) = 0,1x + 20

w(x) = 0,6 * 60 = 36 €
a(x) = 0,2 * 60 + 10 = 22 €
b(x) = 0,1 * 60 + 20 = 26 €

MEGOLDÁS

0,6x > 0,2x + 10
0,4x > 10
x > 25
A 25. perctől lesz a tarifa A olcsóbb mint az értékkártya.

MEGOLDÁS

0,2x + 10 > 0,1x + 20
0,1x > 10
x > 100
A 100. perctől lesz a tarifa B olcsóbb mint a tarifa A.

MEGOLDÁS

F(x) = 0,96x + 2,50
x = 6 km
0,96*6 + 2,5 = 8,26 €
Egy 6 km-es út 8,26 €-ba kerül.

MEGOLDÁS

0,96x + 2,5 = 10
0,96x = 7,5
x = 7,8125 km
10 €-val kb. 7,8125 km utat tehetünk meg.

Feladatok a másodfokú függvényekhez

MEGOLDÁS

$\begin{bmatrix}{x}&{-2}&{-1}&{0}&{1}&{2}\\{f(x)}&{2}&{-1}&{-2}&{-1}&{2}\end{bmatrix}$

MEGOLDÁS FÜGGVÉNYÁBRÁZOLÁS

Megoldások a másodfokú függvényekhez

MEGOLDÁS

$\begin{bmatrix}{x}&{-1}&{0}&{1}&{2}&{3}&{4}&{5}\\{f(x)}&{5}&{0}&{-3}&{-4}&{-3}&{0}&{5}\end{bmatrix}$

MEGOLDÁS FÜGGVÉNYÁBRÁZOLÁS

Megoldások a másodfokú függvényekhez B

MEGOLDÁS

$\begin{bmatrix}{x}&{-2}&{-1}&{0}&{1}&{2}&{3}\\{f(x)}&{8}&{0}&{-4}&{-4}&{0}&{8}\end{bmatrix}$

MEGOLDÁS FÜGGVÉNYÁBRÁZOLÁS

Megoldások a másodfokú függvényekhez C

MEGOLDÁS

$\begin{bmatrix}{x}&{-5}&{-4}&{-3}&{-2}&{-1}&{0}&{1}\\{f(x)}&{4,5}&{2}&{0,5}&{0}&{0,5}&{2}&{4,5}\end{bmatrix}$

MEGOLDÁS FÜGGVÉNYÁBRÁZOLÁS

Megoldások a másodfokú függvényekhez D

MEGOLDÁS

$\begin{bmatrix}{x}&{-2}&{-1}&{0}&{1}&{2}&{3}\{f(x)}&{-5}&{-1}&{1}&{1}&{-1}&{-5}\end{bmatrix}$

$-x^2 + x + 1 = 0 \Rightarrow x = \frac{1}{2}\pm\sqrt{5}$

MEGOLDÁS FÜGGVÉNYÁBRÁZOLÁS

MEGOLDÁS

$\begin{bmatrix}{x}&{-3}&{-2}&{-1}&{0}&{1}\{f(x)}&{-11}&{-4}&{-1}&{-2}&{-7}\end{bmatrix}$

$-2x^2 - 3x - 2 = 0 \Rightarrow nincs$

MEGOLDÁS

$\begin{bmatrix}{x}&{-2}&{-1}&{0}&{1}&{2}\\{f(x)}&{2}&{-1}&{-2}&{-1}&{2}\end{bmatrix}$

MEGOLDÁS FÜGGVÉNYÁBRÁZOLÁS

Megoldások a másodfokú függvényekhez

MEGOLDÁS

$\begin{bmatrix}{x}&{-1}&{0}&{1}&{2}&{3}&{4}&{5}\\{f(x)}&{5}&{0}&{-3}&{-4}&{-3}&{0}&{5}\end{bmatrix}$

MEGOLDÁS FÜGGVÉNYÁBRÁZOLÁS

Megoldások a másodfokú függvényekhez B

MEGOLDÁS

$\begin{bmatrix}{x}&{-2}&{-1}&{0}&{1}&{2}&{3}\\{f(x)}&{8}&{0}&{-4}&{-4}&{0}&{8}\end{bmatrix}$

MEGOLDÁS FÜGGVÉNYÁBRÁZOLÁS

Megoldások a másodfokú függvényekhez C

MEGOLDÁS

$\begin{bmatrix}{x}&{-5}&{-4}&{-3}&{-2}&{-1}&{0}&{1}\\{f(x)}&{4,5}&{2}&{0,5}&{0}&{0,5}&{2}&{4,5}\end{bmatrix}$

MEGOLDÁS FÜGGVÉNYÁBRÁZOLÁS

Megoldások a másodfokú függvényekhez D

MEGOLDÁS

$\begin{bmatrix}{x}&{-2}&{-1}&{0}&{1}&{2}&{3}\\{f(x)}&{-5}&{-1}&{1}&{1}&{-1}&{-5}\end{bmatrix}$

$-x^2 + x + 1 = 0 \Rightarrow x = \frac{1}{2}\pm\sqrt{5}$

MEGOLDÁS FÜGGVÉNYÁBRÁZOLÁS

Megoldások a másodfokú függvényekhez E

MEGOLDÁS

$\begin{bmatrix}{x}&{-3}&{-2}&{-1}&{0}&{1}\\{f(x)}&{-11}&{-4}&{-1}&{-2}&{-7}\end{bmatrix}$

$-2x^2 - 3x - 2 = 0 \Rightarrow nincs$

MEGOLDÁS FÜGGVÉNYÁBRÁZOLÁS

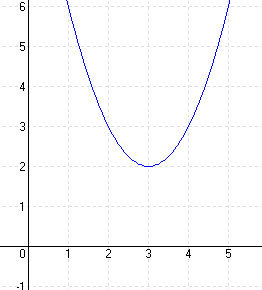
MEGOLDÁS

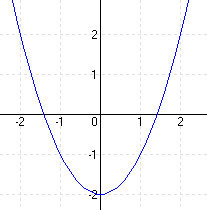
y = x 2 – 6x + 11 = (x – 3) 2 – 9 + 11 = (x – 3) 2 + 2 ⇒ T (3; 2)
(x – 3) 2 + 2 = 0 ⇒ (x – 3) 2 = -2 ⇒ nincs zérushely

Megoldások a másodfokú függvényekhez 2A

MEGOLDÁS

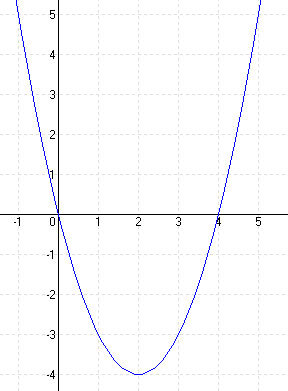
y = x 2 – 2x – 3 = (x – 1) 2 – 1 – 3 = (x – 3) 2 – 4 ⇒ T (1; -4)
(x – 1) 2 – 4 = 0 ⇒ (x – 1) 2 = 4 ⇒ x₁ = 3 és x₂ = -1

Megoldások a másodfokú függvényekhez 2B

MEGOLDÁS

y = x 2 + 4x + 3 = (x + 2) 2 – 4 + 3 = (x + 2) 2 – 1 ⇒ T (-2; -1)
(x + 2) 2 – 1 = 0 ⇒ (x + 2) 2 = 1 ⇒ x₁ = -1 és x₂ = -3

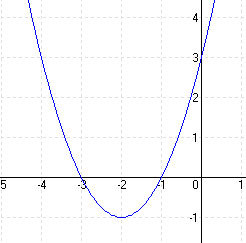
Megoldások a másodfokú függvényekhez 2C

MEGOLDÁS

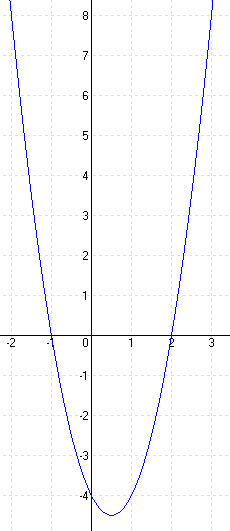
y = x 2 + 5x + 7 = (x + 2,5) 2 – 6,25 + 7 = (x + 2,5) 2 + 0,75 ⇒ T (-2,5; -7,5)
(x + 2,5) 2 + 0,75 = 0 ⇒ (x + 2,5) 2 = -0,75 ⇒ nincs zérushely

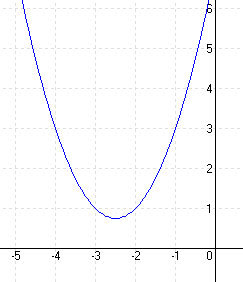
Megoldások a másodfokú függvényekhez 2D

3.) Számold ki a másodfokú függvények egyenletét, melynek grafikonja átmegy a megadott pontokon! Ábrázold a függvényt és számítsd ki a zérushelyeket!

A (0; 2) B (1; 1) C (3; 5)

f : y = ax 2 + bx + c

A ∈ f : 2 = a . 0 2 + b . 0 + c
B ∈ f : 1 = a . 1 2 + b . 1 + c
C ∈ f : 5 = a . 3 2 + b . 3 + c
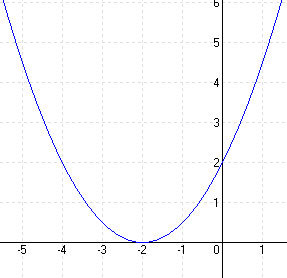
a = 1, b = -2, c = 2, y = x 2 – 2x + 2

MEGOLDÁS

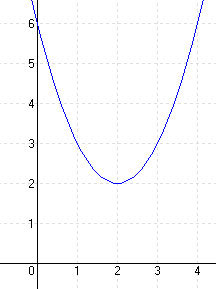
A ∈ f : 6 = a . 0 2 + b . 0 + c ⇒ c = 6
B ∈ f : 3 = a . 1 2 + b . 1 + c ⇒ 3 = a + b + 6 ⇒ -3 – b = a
C ∈ f : 2 = a . 2 2 + b . 2 + c ⇒ 2 = 4a + 2b + 6 ⇒ b = -4
a = 1, b = -4, c = 6, y = x 2 – 4x + 6
Zérushelyek: nincs

Megoldások a másodfokú függvényekhez 3A

MEGOLDÁS

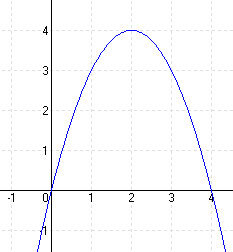
A ∈ f : 0 = a . 0 2 + b . 0 + c ⇒ c = 0
B ∈ f : 4 = a . 2 2 + b . 2 + c ⇒ 4 = 4a + 2b ⇒ b = 2 – 2a
C ∈ f : 3 = a . 3 2 + b . 3 + c ⇒ 3 = 9a + 3b
3 = 9a + 3 . (2 – 2a) = 9a + 6 – 6a ⇒ a = -1
a = 1, b = 4, c = 0, y = -x 2 + 4x
Zérushelyek: x₁ = 0 és x₂ = 4

Megoldások a másodfokú függvényekhez 3B

MEGOLDÁS

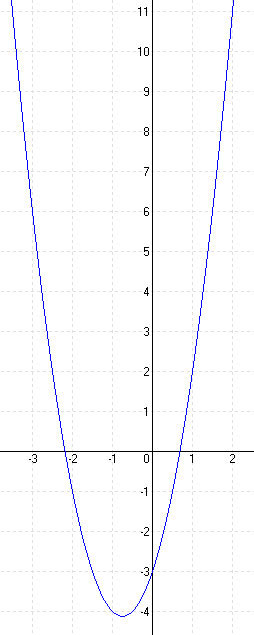
A ∈ f : -4 = a . -1 2 + b . -1 + c ⇒ -4 = a – b + c
-4 = a – b + c ⇒ b = a + 4 + c
B ∈ f : 2 = a . 1 2 + b . 1 + c ⇒ 2 = 2a + 4 + 2c ⇒ -2 = 2a + 2c
-2 = 2a + 2c ⇒ c = -1 – a
C ∈ f : 11 = a . 2 2 + b . 2 + c ⇒ 11 = 4a + 2b + c
11 = 4a + 2b + c = 4a + 2 . (a + 4 c) + c ⇒ 11 = 6a + 8 + 3c
11 = 6a + 8 + 3c = 6a + 8 + 3 . (-1 – a) ⇒ a = 2
c = -1 – 2 = -3
a = 2, b = 3, c = -3, y = 2x 2 + 3x – 3

$x_1 = \frac{-3 + \sqrt33}{4} \hspace{25pt} x_2 = \frac{-3 + \sqrt33}{4}$

Megoldások a másodfokú függvényekhez 3C

MEGOLDÁS

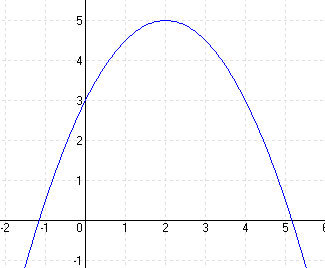
A ∈ f : 4,5 = a . -1 2 + b . -1 + c ⇒ 4,5 = a + b + c ⇒ c = 4,5 – a – b
B ∈ f : 5 = a . 2 2 + b . 2 + c ⇒ 5 = 4a + 2b + c
5 = 4a + 2b + (4,5 – a – b) ⇒ 0,5 = 3a + b
C ∈ f : 3 = a . 4 2 + b . 4 + c ⇒ 3 = 16a + 4b + c
3 = 16a + 4b + (4,5 – a – b) ⇒ – 1,5 = 15a + 3b
-1,5 = 15a + 3b ⇒ b = -0,5 – 5a
0,5 = 3a + b = 3a + (-0,5 – 5a) ⇒

$a = -\frac{1}{2}\hspace{25pt}b = -0,5 - 5 * -\frac{1}{2} = 2$

$a = -\frac{1}{2},\hspace{15pt}b = 2,\hspace{15pt}c = 3,\hspace{15pt}y = -\frac{1}{2}x^2 + 2x + 3$

$x_1 = 2 + {\sqrt3} \hspace{25pt} x_2 = 2 - {\sqrt3}$

Megoldások a másodfokú függvényekhez 3D

Previous Algebra feladatok

Next Van egy 10. bolygó?

KAPCSOLÓDÓ BEJEGYZÉSEK

Szöveges feladatok és megoldások

Feladatok integrálszámítás

Feladatok függvényvizsgálathoz

No Comment

LEGTÖBB HOZZÁSZÓLÁS

Algebra feladatok

Feladatok és megoldások deriválás témakörben

Tudósok, akik szerint van bizonyíték Isten létezésére

Szöveges feladatok és megoldások

Egyenletek – feladatok és megoldások

LEGOLVASOTTABB CIKKEINK

A Quercetin (kvercetin) és a D-vitamin – Szövetségesek a koronavírus ellen?

Kéz-láb-száj vírus – az új gyerekbetegség

Boldogságunk négy forrása: dopamin, endorfin, szerotonin és oxitocin

Agyérkatasztrófák nyomában

A lekopogás babonája

LEGUTÓBBI HOZZÁSZÓLÁSOK

Valcsicsák Zoltán – A Big Mac-index – szemléltethető közgazdaságtan
Kati – Szélsőérték-számítási feladatok
Hargitai Ferenc – Vicces matematika
TudományPláza – Szélsőérték-számítási feladatok
TudományPláza – Boldogságunk négy forrása: dopamin, endorfin, szerotonin és oxitocin

Egészség és életmód

Élővilág

Évezredek

Környezet

Mi magyarok

Mindennapok

Technika

Univerzum

RÓLUNK – TUDOMÁNYPLÁZA

Világunk összes titkát bizonyára sohasem fogjuk megismerni, így mindig érhetnek bennünket meglepetések. A TudományPláza egy olyan online magazin, amely igyekszik mindenki számára elérhetővé és érthetővé tenni a tényeket. Ám, nem szabad elfelejtenünk, hogy minél többet tudunk, annál kevesebbet ismerünk ahhoz képest, amit ismerni szeretnénk.

LEGUTÓBBI TUDOMÁNYOS CIKKEK

Lovas kvíz – Lovakról szakszerűen. Ismered ezeket az információkat?

Endospórák elektrokémiai állapotváltozása

Új felvételi pontrendszer

Hogyan válasszunk gyerekforgószéket?

Videó, ÉRDEKESSÉGEK

Don’t miss

Lovas kvíz – Lovakról szakszerűen. Ismered ezeket az információkat?

Endospórák elektrokémiai állapotváltozása

Új felvételi pontrendszer

Azért, hogy megkönnyítsük látogatóink számára a weboldal használatát, oldalunk cookie-kat, ismert nevén sütiket használ.
Weboldalunk böngészésével Ön beleegyezik, hogy a számítógépén, illetve mobil eszközén cookie-kat tároljunk. Elfogadom Információ

Privacy Overview

This website uses cookies to improve your experience while you navigate through the website. Out of these, the cookies that are categorized as necessary are stored on your browser as they are essential for the working of basic functionalities of the website. We also use third-party cookies that help us analyze and understand how you use this website. These cookies will be stored in your browser only with your consent. You also have the option to opt-out of these cookies. But opting out of some of these cookies may affect your browsing experience.

Necessary cookies are absolutely essential for the website to function properly. This category only includes cookies that ensures basic functionalities and security features of the website. These cookies do not store any personal information.

Any cookies that may not be particularly necessary for the website to function and is used specifically to collect user personal data via analytics, ads, other embedded contents are termed as non-necessary cookies. It is mandatory to procure user consent prior to running these cookies on your website.

GEOMATECH tananyagok

A tananyagegység célja a függvények ábrázolásának gyakoroltatása.

Az alkalmazás nehézségi szintje, tanárként

Könnyű, nem igényel külön készülést.

Módszertani megjegyzés, tanári szerep

A tanegység többféleképpen használható:

dolgozat feladathoz is készíthetünk ábrát az interaktív anyagot használva (rajzlap, mint kép mentése).
értékpárokat leolvasva találják ki a diákok, hogy mi a hozzárendelési utasítás (lineáris függvény esetében ez jó bevezetés is lehet).
függvény transzformációk gyakoroltatására is hasznos segítség lehet:
- egy adott típus-függvény transzformáltjai
- egy adott transzformáció megfigyelése különböző alapfüggvények esetén
FIGYELEM! Jelenleg nincs mód a nyílt és zárt intervallumok jelölésére. Ez például az egészrész-, szignum- és a törtrészfüggvények grafikonja esetében meggondolást igényel. A csoporttól függhet, hogy elmondva a magyarázatot érdemes-e így ábrázolni ilyen jellegű függvényeket, vagy a végpontok megfelelő jelölésének hiánya problémássá teheti számukra a megértést.

Felhasználói leírás

MÉLYVÍZ A FÜGGVÉNYEK TENGERÉN.
Függvények grafikonjának ábrázolását gyakorolhatod az alábbi alkalmazással.
A függvényeket az alábbi képletek segítségével tudod megadni:

Függvények ábrázolása

Adott az $f: A \mapsto B$ függvény. A függvény értelmezési tartománya azoknak az elemeknek a halmaza az $A$ halmazban, amikhez a függvény hozzárendel $B$ halmazbeli elemeket.

Az értelmezési tartományt az angol domain szó alapján, ami egyébként azt jelenti, hogy tartomány, így jelöljük: $D_f$.

De a gyengébb idegzetűek kedvéért szokás úgy is jelölni, hogy É.T.

Függvény fogalma

Adott az $A$ és $B$ nem üres halmaz.

Ha az $A$ halmaz bizonyos elemeihez egyértelműen hozzárendeljük a $B$ halmaz bizonyos elemeit, akkor ezt a hozzárendelést függvénynek nevezzük.

Kölcsönösen egyértelmű hozzárendelés

Az $f: \; x\mapsto y$ függvény kölcsönösen egyértelmű, ha $x_1 \neq x_2$ akkor $y_1 \neq y_2$. Vagyis különböző $x$-ekhez mindig különböző $y$-okat rendel.

Zérushely

Azokat a pontokat, ahol a függvény grafikonja az $x$ tengelyt metszi, zérushelynek nevezzük.

Függvény konvexitása

Konkávnak nevezzük a függvényt azon a szakaszon, ahol “szomorú hangulatban” van, vagy precizebben ha a szakaszon a függvény bármely két pontját összekötve a függvény a két pontot összekötő egyenes felett halad.

Konvexnek nevezzük a függvényt azon a szakaszon, ahol “vidám hangulatban” van, vagy precizebben ha a szakaszon a függvény bármely két pontját összekötve a függvény a két pontot összekötő egyenes alatt halad.

Függvény monotonitása

Az $f(x)$ függvényt egy $]a,b[$ intervallumon monoton növekedőnek mondunk, ha bármely $x_1, x_2 \in ]a,b[$ esetén, ha $x_1 < x_2$, akkor $f(x_1) \leq f(x_2) $

Szigorúan monoton növekedő, ha bármely $x_1, x_2 \in ]a,b[$ esetén, ha $x_1 < x_2$, akkor $f(x_1) < f(x_2) $

Az $f(x)$ függvényt egy $]a,b[$ intervallumon monoton csökkenőnek mondunk, ha bármely $x_1, x_2 \in ]a,b[$ esetén, ha $x_1 < x_2$, akkor $f(x_1) \geq f(x_2) $

Szigorúan monoton csökkenő, ha bármely $x_1, x_2 \in ]a,b[$ esetén, ha $x_1 < x_2$, akkor $f(x_1) >f(x_2) $

Függvény szélsőértéke

Függvény szélsőértékén a maximumát illetve minimumát értjük.

Az $f(x)$ függvénynek az $x_0 \in D_f$ pontjában (globális) maximuma van, ha minden $x\in D_f$ esetén $f(x) \leq f(x_0)$.

Az $f(x)$ függvénynek az $x_0 \in D_f$ pontjában (globális) minimuma van, ha minden $x\in D_f$ esetén $f(x) \geq f(x_0)$.

Az $f(x)$ függvénynek az $x_0 \in D_f$ pontjában lokális maximuma van, ha létezik olyan nem nulla környezete, hogy ott ő a maximum.

Az $f(x)$ függvénynek az $x_0 \in D_f$ pontjában lokális minimuma van, ha létezik olyan nem nulla környezete, hogy ott ő a minimum.

Függvénytranszformációk

Belső függvénytranszformáció: $f(x+a)$, ez úgy működik, hogy az $x$ tengely mentén tolja el a függvény grafikonját.

Külső függvénytranszformáció: $f(x)+a$, ez pedig az $y$ tengelyen tolja el a függvényt.

Függvény szorzása számmal: $a\cdot f(x)$, ilyenkor megnyújtjuk a függvényt az $y$ tengely szerint.

Függvény változójának szorzása egy számmal: $f(a \cdot x)$, ilyenkor az $x$ tengely szerint nyújtjuk a függvényt.

Függvények paritása

Minden olyan függvényt, ami az $y$ tengelyre szimmetrikus, páros függvénynek hívunk. Ezek a függvények azt tudják, hogy bármely $x$-re amelyre értelmezve vannak:

Azokat a függvényeket, amelyek az origóra szimmetrikusak, páratlan függvénynek nevezzük. A páratlan függvények úgy működnek, hogy bármely $x$-re amelyre értelmezve vannak:

Polinomfüggvény

Ha az $x$ különböző pozitív egész kitevős hatványait összeadjuk vagy kivonjuk, akkor polinomokat kapunk.

A polinomfüggvény általános alakja:

$ f(x) = a_n x^n + a_ x^ + \dots a_1 x + a_0 $

A legmagasabb fokú tag együtthatóját hívjuk főegyütthatónak.

Adott a következő függvény.

$ f(x)=x^2-4 \quad D_f : -2 \leq x \leq 4 $

a) Milyen számot rendel hozzá ez a függvény a 3-hoz?

b) Melyik az a szám, amihez a függvény a 12-t rendeli hozzá?

c) Mik a függvény zérushelyei?

Ábrázoljuk az alábbi függvényeket.

Ábrázoljuk a következő függvényeket.

Ábrázoljuk az alábbi függvényeket.

Ábrázoljuk a következő függvényeket.

Ábrázoljuk az alábbi függvényeket.

Ábrázoljuk az alábbi függvényeket.

Ábrázoljuk az alábbi függvényeket.

Ábrázoljuk az alábbi függvényeket.

Ábrázoljuk az alábbi függvényeket.

Ábrázoljuk az alábbi függvényeket.

Ábrázoljuk az alábbi függvényeket.

13. Ábrázoljuk az alábbi függvényeket.

Ábrázoljuk az alábbi függvényeket.

Ábrázoljuk az $f(x)=|x-3|-5 $ függvényt.

Ábrázoljuk az $f(x)=-|x+1|+2 $ függvényt.

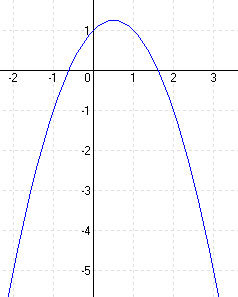
Ábrázoljuk az $f(x)=-(x-2)^2+1 $ függvényt.

Ábrázoljuk az $f(x)=(x-2)^2+5 $ függvényt.

Ábrázoljuk az $f(x)=-|x+2|+3 $ függvényt.

Ábrázoljuk az $f(x)=x^2-6x+13 $ függvényt.

Ábrázoljuk az $f(x)=|x+2|-3 $ függvényt.

Ábrázoljuk az $f(x)=x^2+2x+4 $ függvényt.

Ábrázoljuk az $f(x)=x^2-10x+20 $ függvényt.

Ábrázoljuk az $f(x)=\frac $ függvényt.

Ábrázoljuk az $f(x)=\frac+5 $ függvényt.

Itt röviden és szuper-érthetően meséljük el neked, hogy, hogyan kell függvényeket ábrázolni. Függvények, koordináták, Értelmezési tartomány, Értékkészlet, Transzformációk, Külső és belső függvény transzformációk, x tengelyre tükrözés, y tengelyre tükrözés, néhány fontosabb függvény, mindez a középiskolás matek ismétlése. Szó lesz aztán a függvények monotonitásáról, konvexitásáról, lokális és abszolút szélsőértékekről, a függvények értelmezési tartományáról és értékkészletéről. Megnézzük a másodfokú függvények ábrázolását. A másodfokú függvények grafikonja egy parabola. A parabola csúcspontja eredetileg az origoban van, de ha eltoljuk a függvény grafikonját a függvénytranszformációkkal, akkor a csúcspont is arrébb tolódik. Nézzük meg, hogy hova, és azt is, hogy miért. Aztán jönnek a polinomfüggvények. Megtudhatod, hogyan néz ki az x a köbön függvény, az x a negyediken függvény és általában a hatványfüggvények. Megnézzük mi a közös a páros kitevős hatványfüggvényekben és a páratlan kitevős hatványfüggvényekben. Aztán megnézzük a páros és páratlan kitevős polinomfüggvényeket. Végül jön néhány polinomfüggvényes feladat a polinomfüggvények ábrázolásával és zérushelyeivel kapcsolatban. Ezek után jön a négyzetgyök függvény és különböző transzformációi. Aztán megnézzük az abszolútérték függvényt. Majd következik az 1/x függvény, amelynek grafikonja a hiperbola.

Az x2 függvény grafikonja egy parabola.

A parabola csúcsa az origóban van.

Nézzük, mi történik akkor…

ha itt a zárójelen belül levonunk 3-at.

Ennek hatására a parabola eltolódik 3-mal.

A parabola csúcsa mindig oda tolódik,

Ez pedig akkor nulla, ha x=3.

Ebből tehát látjuk, hogy 3-mal tolódik el…

és azt is látjuk, hogy az x tengelyen.

Olyankor, amikor a 3-at így vonjuk le…

egészen más dolog történik.

Ilyenkor az y tengelyen tolódik 3-mal lefelé.

Az izgalmak növelése érdekében most nézzük, mi van akkor, ha ezt a két dolgot egyszerre csináljuk…

Kezdjük ezzel a résszel itt…

Aztán itt van még ez is.

Ezt úgy hívjuk, hogy belső függvény-transzformáció.

És úgy működik, hogy az x tengely mentén tolja el a függvény grafikonját.

A külső függvény-transzformáció a zárójelen kívül van itt.

Ez pedig az y tengelyen tolja el a függvényt.

Hogyha itt van például ez a függvény:

A belső transzformáció miatt az x tengely mentén eltolódik…

Egészen pontosan ide.

Az y tengely mentén pedig ide.

Most nézzük, mi a helyzet ezzel:

Ez pontosan ugyanúgy néz ki, mint az x2, csak éppen a kétszeresére nyújtva.

Az is megeshet, hogy a háromszorosára nyújtjuk…

Vagy éppen a mínusz kétszeresére.

És az is előfordulhat, hogy egyetlen függvényben minden eddigi rémség egyszerre van benne.

Végül itt jön még ez is:

De szenvedéseink tovább folytatódnak…

Néhány izgalmas kísérletet fogunk elvégezni a függvény segítségével.

Ha a elé írunk egy mínusz jelet, akkor ezzel a függvény grafikonját az x tengelyre tükrözzük.

Hogyha pedig belülre rakjuk a mínuszjelet, akkor az y tengelyre tükrözzük.

És ha kedvünk van, tükrözhetjük a függvényt

mindkét tengelyre is.

Lássuk, hogyan néz ki például ez…

A gyökjel előtt nincsen mínuszjel…

Itt belül az x előtt viszont igen.

Na persze még el is van tolva…

Megnézzük, hogy ez itt belül mikor nulla…

Úgy néz ki, hogy 4-gyel tolódik el az x tengelyen.

2-vel pedig fölfelé.

És talán még egy utolsó nem árthat meg:

A parabolát is pontosan ugyanígy tudjuk tükrözni a tengelyekre.

Hogyha az x2 elé írjuk a mínusz jelet, akkor a függvény grafikonját az x tengelyre tükrözzük.

Hogyha pedig a zárójelen belülre rakjuk a mínuszjelet, akkor az y tengelyre tükrözzük.

Csak sajnos ez nem igazán látszik…

mert a parabola az y tengelyre szimmetrikus.

Ezért is végeztük az iménti kísérleteinket a függvényen.

De azért így a végén még nézzük meg ezt:

Hát így kezdetnek ennyit a függvény-transzformációkról.

Ha az x különböző hatványait összeadjuk, akkor polinomokat kapunk.

Ez itt például az x5.

És, ha kivonjuk belőle azt, hogy x3…

akkor egy ilyen kanyargós polinomfüggvényt kapunk.

Íme, itt a polinomfüggvények általános alakja.

A polinomfüggvények viselkedése

A legmagasabb fokú tag együtthatóját hívjuk főegyütthatónak.

És a legmagasabb fokú tag határozza meg a polinomfüggvény viselkedését.

Ha a legmagasabb fokú tag kitevője páros és a főegyüttható pozitív, akkor így néz ki a polinomfüggvény.

Ha a főegyüttható negatív, akkor ilyen.

A páratlan fokú polinomfüggvények egészen máshogy néznek ki.

Ha a főegyüttható pozitív, akkor innen lentről mennek fölfelé…

Ha negatív, akkor pedig fentről mennek lefelé.

Egy páros fokú polinomfüggvény megteheti, hogy sohasem metszi az x tengelyt.

De egy páratlan fokúnak legalább egyszer biztosan metszenie kell.

Ezért van az, hogy egy páratlan fokú polinomfüggvénynek mindig van zérushelye.

Most pedig néhány művészi rajzot fogunk készíteni.

Kezdjük egy olyan harmadfokú polinomfüggvénnyel, aminek pontosan két zérushelye van.

Egy harmadfokú polinomfüggvénynek legalább egy zérushelye biztosan van.

És maximum három tud lenni.

De egy kis trükk segítségével azért megoldható a kettő is.

Művészi pályafutásunk következő darabja egy olyan negyedfokú polinomfüggvény, aminek három zérushelye van.

Egy negyedfokú polinomfüggvénynek lehet nulla zérushelye…

aztán lehet egy is.

Sőt lehet négy is.

De négynél több már nem.

Egy n-edfokú polinomfüggvénynek mindig legfeljebb n darab zérushelye tud lenni.

Ha a fokszám páratlan, akkor 1-től n-ig bármennyi lehet.

Ha a fokszám páros, akkor pedig 0-tól n-ig bármennyi.

Most éppen azt szeretnénk, hogy három zérushely legyen.

És íme, itt is van.

Próbáljuk meg kideríteni, hogy a három grafikon közül melyik tartozik ehhez a polinomfüggvényhez.

Az első grafikon ez a típus.

Egy páratlan fokú polinomfüggvény.

A mi kis függvényünk viszont negyedfokú.

A másik kettő már jobbnak tűnik.

Az ilyen extra kanyarokhoz viszont…

itt még lennie kéne valaminek.

Így hát a nyertes a középső.

Nézzünk meg még egyet.

Döntsük el, hogy a három grafikon közül melyik tartozik ehhez a polinomfüggvényhez.
Related posts:

Másodfokú függvény feladatok megoldással