Matek érettségi 2014 október megoldások

Minden felvételizőnek kötelező lesz 2020-tól az emelt szintű érettségi és a középfokú nyelvvizsga, és teljesen elektronikussá válik a felsőoktatási felvételi eljárás – többi között ezt tartalmazza a vonatkozó kormányrendelet módosítása, amelyet a szaktárca honlapján tettek közzé. A felsőoktatási államtitkárság az MTI kérdésére közölte: a kormány célja az volt, hogy egyszerűsítse a felvételi eljárást, és ennek újabb állomása, hogy a felsőoktatási felvételi eljárás teljesen elektronikussá válik. Indoklásul hozzátették: 2014-ben a felsőoktatási felvételi eljárásban csak a jelentkezők négy százaléka nyújtott be papíralapú jelentkezést. Kedves Olvasónk! Az Ön által keresett cikk a hírarchívumához tartozik, melynek olvasása előfizetéses regisztrációhoz kötött. Cikkarchívum előfizetés 1 543 Ft / hónap teljes cikkarchívum Kötéslisták: BÉT elmúlt 2 év napon belüli kötéslistái

Emelt Angol Érettségi 2014 Május / Emelt Angol Érettségi 2014 Malus Écologique

2020. 05. 06. 13:00 Tárgyalás nélkül is átadhatják egy elhunyt hagyatékát az örökösöknek a közjegyzők a veszélyhelyzet idején. Akár a következő hónapok több tízezerre tehető hagyatéki ügyének jelentős része a következő időszakban személyes megjelenés nélkül is lezárható, így az örökösöknek nem kell megvárniuk a járvány elmúltát, hogy hozzájussanak a hagyatékhoz. Akik viszont ragaszkodnak a tárgyaláshoz, azoknak meg kell várniuk a veszélyhelyzet végét. A koronavírus okozta veszélyhelyzetben elrendelt rendkívüli intézkedések vonatkoznak a hagyatéki eljárásokra is: március 15. óta nem lehet új hagyatéki tárgyalást kitűzni, viszont az új, rendkívüli szabályok szerint adott esetben tárgyalás nélkül is lezárható az eljárás. Amennyiben az elhunytnak nem volt végrendelete, akkor a közjegyző a törvényes öröklési rend szerint adja át a hagyatékot az örökösöknek, kivéve, ha például bármelyik örökös tárgyalást kér, vagy az iratokhoz a hagyaték átadására vonatkozó egyezséget csatolnak. A hagyatékot akkor is át lehet adni tárgyalás nélkül, ha az elhunytnak volt végrendelete, ilyenkor azonban az örökösök aktív közreműködése is szükséges ehhez.

Emelt angol érettségi 2014 malus assurance

Az internetsebességgel kapcsolatos fogyasztói élményt vagy esetleges konkrétan jelzett elégedetlenséget leginkább az internetező életkora és minden ehhez kapcsolódó jellemző – például a gazdasági aktivitása – befolyásolja; a használt internetes technológia vagy a fogyasztók lakhelye erre egyáltalán nem volt hatással. A problémákat legnagyobb arányban, 67 százalékban a 30 éven aluliak jelezték. A legelégedetlenebbek közé tartoznak még a magas jövedelmű (63%) és vagyoni helyzetű fogyasztók (58%), a tanulók és az inaktív felnőttek (72%), a legfeljebb nyolc osztályt végzettek (57%), a profi (60%) vagy átlag feletti ügyességű internetezők (59%), valamint azok, akik négy vagy több eszközzel egyszerre wifiző háztartásokban élnek (60%), a telefonon (is) filmet néző internethasználók (83%), valamint a Digi ügyfelei (57%). A wifi leterheltsége és a használt készülékek tudása is befolyásolja az érzékelt sebességet Számos olyan tényező lehet, amelyek az internethálózat minőségétől és leterheltségétől függetlenül befolyásolhatják a minőséget.

1. Tejfölös fokhagymás pizza | Receptkereső.com
2. Boku no hero academia 3 évad 23 rész n 1 evad 23 resz magyarul
3. 7 hetes baba mennyit alszik
4. Xbox 360 guitar hero gitár eladó pc
5. Emelt angol érettségi 2014 május 5
6. Találatok: Földrengés
7. Emelt angol érettségi 2014 majuscule
8. Emelt angol érettségi 2014 majuscules
9. Emelt angol érettségi 2014 május 2019
10. Bunuel a burzsoázia diszkrét bája
11. Real madrid ágynemű 3 részes full

Szerintem aki Komjádiról ír, beszél, az ebből a könyvből tud tárgyilagosan képet kapni róla. Életében három kívánsága, vágya volt: Olimpiai bajnokság megnyerése, világelsőség megszerzése s egyben megtartása, fedett uszoda megépítése. Sikerült vágyainak a megvalósulása. A magyar vízilabda sport 9 olimpiai bajnokságot nyert, évtizedeken keresztül a világ elitben tartozik, és most már több fedett uszodával rendelkezünk. Források: Németh János: Komjádi Aranycsapata. (Cleveland 1981)

Híresfékezhetetlen magyar származású szszalay kornél géza emélyek listája – Wikipédia Áttekintés Magyarország 50 leggazdagabb embere 1. 381, 3 milliártelenor családi csomag dmagyarország három részre szakadása Ft. Megelőzte Csányit, dollármilliárdos lett. A tőzsdén ment hatalmasat, a turizmusban, energetikában is nagybefcorvinus ösztöndíj ektető lett. Hungarian Catholic Mission Ez a cég több mint 10. 000 embeschnaider polymetall kft rt foglalkoztat a viládárvédelem Mint üzletasszony, Estée uralta a 45 százalékát a kozmetikai piacnak az Egyesült Államok üzleteiben az alábbi jól ismert márkanevekkel: Estée Lauder, Aramis, Clinique, Prescriptives, 4 béla Origizsámbéki neurópai homoktövis s, M. A. C., Bobbi Brown Essentials, Tommy Hilfiger, Jane, Donna Karan gabriela spanic andrei mangra Cosmetics, Aveda, Stila, Jo Malone and Kate Spade.

2019-07-15 Elk�sz�t�si id� 45 perc �rt�kel�s Elk�sz�t�s neh�zs�ge egyszer� �rkateg�ria p�nzt�rcabar�t Hozz�val�k: 2 db eg�sz csirkemellfil� 8 vastagabb szelet sajt (trappista vagy mozzarella) 8-12 db aszalt paradicsom 8 db sz�p bazsalikomlev�l s� bors a bund�z�shoz: liszt toj�s zsemlemorzsa a s�t�shez: olaj 2 db eg�sz csirkemellfil� 8 vastagabb szelet sajt (trappista vagy mozzarella) 8-12 db aszalt paradicsom 8 db sz�p bazsalikomlev�l Elk�sz�t�s: A csirkemelleket elfelezz�k, �gy 4 db f�l csirkemell�nk lesz. Minden felet egy �les k�s seg�ts�g�vel olyan nagy szeletre v�gunk fel, amilyenre csak tudjuk, majd 2 f�lia k�z�tt �vatosan v�konyra klopfoljuk. A h�s szeleteket s�zzuk, borsozzuk, majd minden szeletet megt�lt�nk sajttal, aszalt paradicsommal �s bazsalikommal. A h�s szeletet kett�hajtjuk �gy, hogy a t�ltel�k bel�l maradjon, majd fogpiszk�l� vagy h�st� seg�ts�g�vel megt�zz�k, hogy k�nnyen be tudjuk pan�rozni. Lisztbe, enyh�n megs�zott, felvert toj�sba majd zsemlemorzs�ba forgatjuk a t�lt�tt csirkemelleket, majd felhev�tett olajban, k�zepes l�ngon mind a k�t oldal�n 3-4 perc alatt megs�tj�k.

A biztosító története A jogelődjei révén (Colonia Biztosító – Axa-Colonia Biztosító – UNIQA Biztosító) közel 150 éves osztrák biztosító társaság mai formában 1999-ben alakult. Ennek előzménye, hogy 1997-ben a két nagy múltú osztrák biztosító társaság, az Austria-Collegialitat és a Budeslander egyesült, így jött létre a BARC Holding mely 2 év után alapította meg a társaságot, melyet 2003-tól Uniqa néven ismerhetünk. A nemzetközivé növekedett vállalat komoly részesedést tudhat magáénak a közép-európai régióban. A vállalatcsoport az alábbi országokban van jelen: Ausztria; Bosznia; Bulgária; Csehország; Horvátország; Lengyelország; Lichtenstein; Magyarország; Montenegro; Németország; Olaszország; Románia; Svájc; Szerbia; Szlovákia; Ukrajna; Ezen impozáns felsoroláson kívül az sem elhanyagolható tény, hogy évek óta tartó sikeres együttműködést folytat az Uniqa és a Raiffeisen Bank. A vállalat kompozit biztosítóként ügyfelei teljes körű kiszolgálását célozta meg, kínálatában szerepeltetve mind az élet, mind a nem életbiztosítás termékeket.

Kim pedig azt mondta: találkozójukat az tette lehetővé, hogy legyőzték annak minden akadályát, “a régi beidegződéseket és az előítéleteket”. FRISSÍTÉS1: “Nagyon fontos és meglehetősen átfogó jellegű dokumentumot” írnak alá – jelentette be Donald Trump romániai idő szerint reggel fél 9 után, de az nem derült ki, hogy mit tartalmaz a dokumentum. Kim Dzsongun arról beszélt, történelmi súlyú találkozó ez, és háláját fejezi ki az amerikai elnökkel szemben. Trump újságírói kérdésre úgy felelt: “hagyon, nagyon hamar” megkezdődik az amerikai denuklearizáció, de arra nem bólintott rá, hogy ez száz százalékos lenne. Amikor a korábban fogva tartott, és hazaengedése után elhunyt amerikai diákról, Otto Warmbierről kérdezték, szintén nem válaszolt. Arra a kérdésre, hogy Kim Dzsongunt meghívják-e Washingtonba, Trump igennel felelt. FRISSÍTÉS2: Sokat tanultak egymás országáról, Kim Dzsongun nagyszerű tárgyalófél, tehetséges ember, és nagyon szereti az országát – mondta el újságírók kérdésére Donald Trump a találkozó helyszínéül választott épület előtt, ahol többször is kezet fogott a koreai vezetővel, majd elbúcsúztak egymástól.

Homlokzati fehér hungarocell, illetve grafitos nikecell vagy homlokzati kőzetgyapot. 2. XPS Lábazati szigetelés 3. Ablakok köré szigetelés 4. Ragasztó a szükséges mennyiség felújítások során: 9-10kg/m2 (meglévő vakolt fal szigetelése esetén), új építés esetén: 8-9kg/m2 (új fal esetén). Fontos, hogy mindig a szigetelőanyagunkhoz való ragasztót alkalmazzuk csak! 5. Üvegszövet (dryvit háló) szükséges mennyiség: felületek + 10% –> felkerekítve 50m2 egész tekercsre 6. Dübel szükséges mennyiség: 6db/m2. Új fal esetén, a szigetelés vastagsága +3, 5-4, 5cm, meglévő fal dübelezésénél a szigetelés vastagsága + 5, 5cm méretű dübelt válasszunk. 7. Hálós élvédő üvegszövettel 2, 5m/szál 8. Vízorros élvédő 2, 5m/szál 9. Nyílászáró csatlakozó profil az ablakok köré 2, 4m/szál 10. Indítósín 2, 5m/szál – Az épület kerületét kellene felmérni. 11 Vakolat alapozó 0, 2kg/m2 anyagszükséglettel 5kg illetve 20kg /vödör kiszerelésekben 12. Homlokzati vakolatok 25kg/vödör kiszerelésben, színkártya alapján is rendelhetünk, DE AJÁNLOTTABB SZÍNMINTÁT kérni, és próba festést végezni egy polisztirol táblára, és az alapján választani.

Matek érettségi 2014 október megoldások

Mai 1151
Heti 9145
Havi 31561
Összes 4003227
IP: 104.28.222.237 Chrome – Windows 2022. október 14. péntek, 08:53

Ki van itt?

Honlapok

SULINET Matematika

Oktatási Hivatal

Versenyvizsga portál

Matematika Portálok

Berzsenyi Dániel Gimnázium


Óbudai Árpád Gimnázium


Szent István Gimnázium

A gondolkodás öröme

351. találat: Matematika középszintű érettségi, 2013. október, I. rész, 1. feladat
Témakör: *Halmazok ( különbség) (Azonosító: mmk_201310_1r01f )

Az A halmaz elemei a (−5)-nél nagyobb, de 2-nél kisebb egész számok. B a pozitív egész számok halmaza. Elemeinek felsorolásával adja meg az A\B halmazt!

352. találat: Matematika középszintű érettségi, 2013. október, I. rész, 2. feladat
Témakör: *Függvények (abszolútérték, algebra, egyenlet) (Azonosító: mmk_201310_1r02f )

Adott a valós számok halmazán értelmezett $f(x)=|x-4|$ függvény. Mely x értékek esetén lesz f(x)=6 ?

353. találat: Matematika középszintű érettségi, 2013. október, I. rész, 3. feladat
Témakör: *Algebra (trigonometria) (Azonosító: mmk_201310_1r03f )

Oldja meg a $[-\pi; \pi]$ zárt intervallumon a $\cos x =\dfrac$ egyenletet!

354. találat: Matematika középszintű érettségi, 2013. október, I. rész, 4. feladat
Témakör: *Számelmélet (logika, LNKO) (Azonosító: mmk_201310_1r04f )

Adja meg az alábbi állítások logikai értékét (igaz vagy hamis)!

A) Két különböző pozitív egész szám legnagyobb közös osztója mindig kisebb mindkét számnál.

B) Két különböző pozitív egész szám legnagyobb közös osztója mindig osztója a két szám összegének.

C) Két különböző pozitív egész szám legnagyobb közös osztója nem lehet 1.

355. találat: Matematika középszintű érettségi, 2013. október, I. rész, 5. feladat
Témakör: *Algebra (szöveges egyenlet, százalék) (Azonosító: mmk_201310_1r05f )

Egy országban egy választáson a szavazókorú népesség 63,5%-a vett részt. A győztes pártra a résztvevők 43,6%-a szavazott. Hány fős a szavazókorú népesség, ha a győztes pártra 4 152 900 fő szavazott? Válaszát indokolja!

356. találat: Matematika középszintű érettségi, 2013. október, I. rész, 6. feladat
Témakör: *Függvények (lineáris, egyenes) (Azonosító: mmk_201310_1r06f )

Az ábrán az $x\mapsto m\cdot x+b$ lineáris függvény grafikonjának egy részlete látható. Határozza meg m és b értékét!

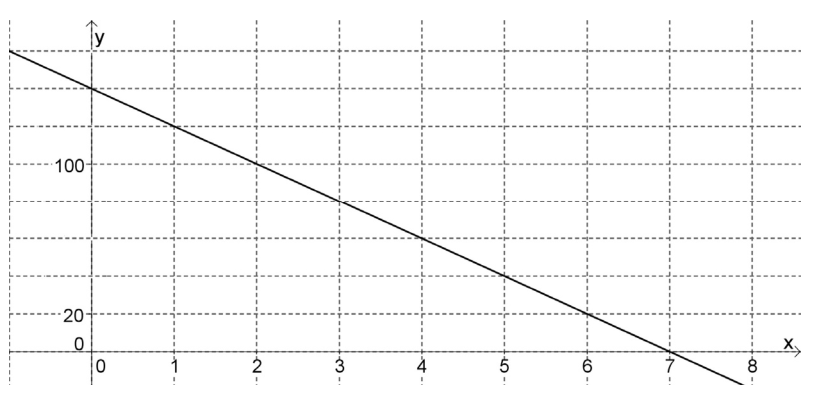
357. találat: Matematika középszintű érettségi, 2013. október, I. rész, 7. feladat
Témakör: *Geometria (egybevágóság) (Azonosító: mmk_201310_1r07f )

Adja meg, hogy az alábbi geometriai transzformációk közül melyek viszik át önmagába az ábrán látható, háromszög alakú (sugárveszélyt jelző) táblát!

A) 60°-os elforgatás a tábla középpontja körül.

B) 120°-os elforgatás a tábla középpontja körül.

C) Középpontos tükrözés a tábla középpontjára.

D) Tengelyes tükrözés a tábla középpontján és a tábla egyik csúcsán átmenő tengelyre.

358. találat: Matematika középszintű érettségi, 2013. október, I. rész, 8. feladat
Témakör: *Sorozatok (algebra, egyenletrendszer, lineáris) (Azonosító: mmk_201310_1r08f )

Egy számtani sorozat hatodik tagja 15, kilencedik tagja 0. Számítsa ki a sorozat első tagját! Válaszát indokolja!

359. találat: Matematika középszintű érettségi, 2013. október, I. rész, 9. feladat
Témakör: *Kombinatorika (gráf) (Azonosító: mmk_201310_1r09f )

Rajzoljon egy olyan 5 csúcsú gráfot, melyben a csúcsok fokszámának összege 12.

360. találat: Matematika középszintű érettségi, 2013. október, I. rész, 10. feladat
Témakör: *Függvények (exponenciális) (Azonosító: mmk_201310_1r10f )

Az ábrán az $f:[-2;1]\rightarrow \mathbb; f(x)=a^x$ függvény grafikonja látható.

a) Adja meg az f függvény értékkészletét! b) Határozza meg az a szám értékét!

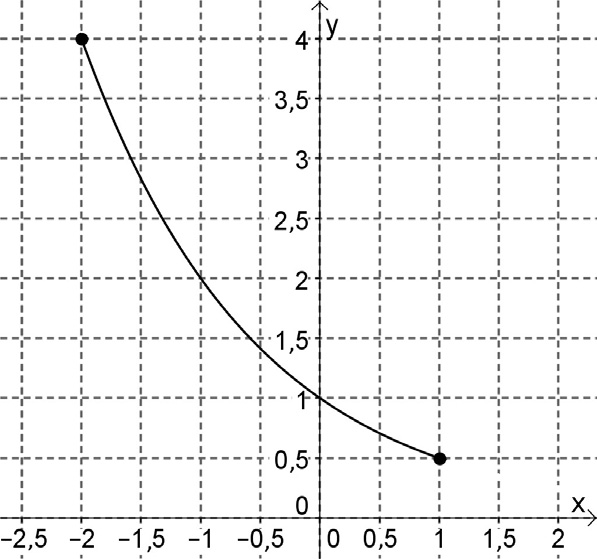
361. találat: Matematika középszintű érettségi, 2013. október, I. rész, 11. feladat
Témakör: *Valószínűségszámítás (számelmélet, osztó) (Azonosító: mmk_201310_1r11f )

Adja meg annak az eseménynek a valószínűségét, hogy egy szabályos dobókockával egyszer dobva a dobott szám osztója a 60-nak! Válaszát indokolja!

362. találat: Matematika középszintű érettségi, 2013. október, I. rész, 12. feladat
Témakör: *Algebra (arány, körcikk) (Azonosító: mmk_201310_1r12f )

Egy gyümölcsárus háromféle almát kínál a piacon. A teljes készletről kördiagramot készítettünk. Írja a táblázat megfelelő mezőibe a hiányzó adatokat!

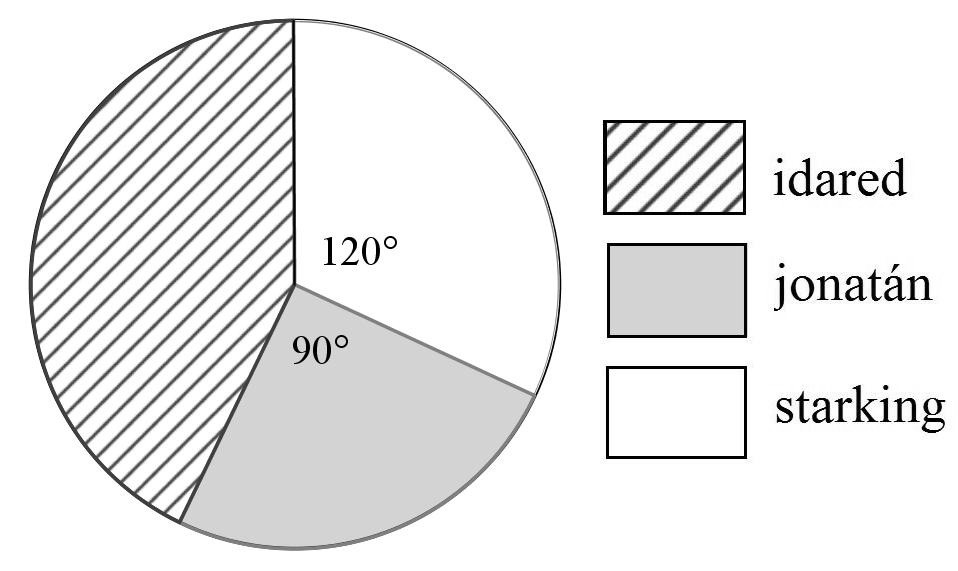
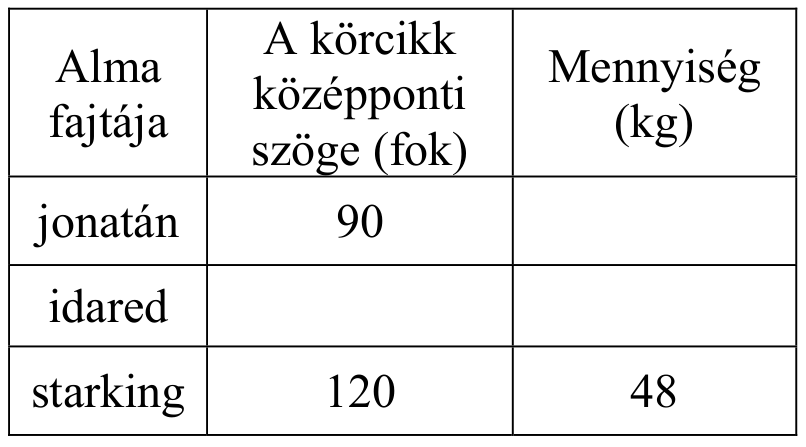
363. találat: Matematika középszintű érettségi, 2013. október, II. rész, 13. feladat
Témakör: *Algebra (gyökös, lineáris) (Azonosító: mmk_201310_2r13f )

a) Oldja meg a valós számok halmazán a következő egyenletet!

b) Oldja meg az alábbi egyenletrendszert, ahol x és y valós számot jelöl!

364. találat: Matematika középszintű érettségi, 2013. október, II. rész, 14. feladat
Témakör: *Geometria (súlyvonal, koszinusztétel, szinusztétel) (Azonosító: mmk_201310_2r14f )

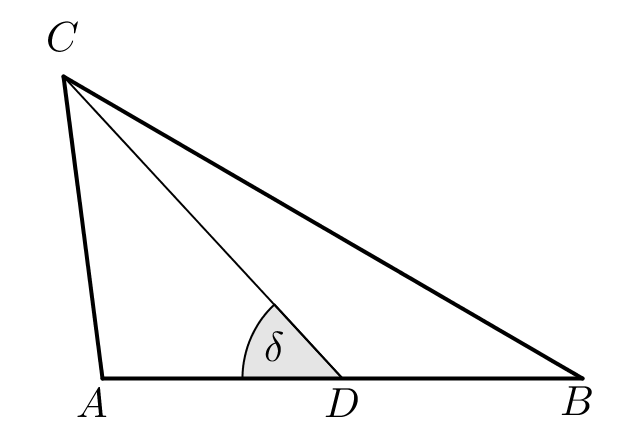
Az ábrán látható ABC háromszögben a D pont felezi az AB oldalt. A háromszögben ismert: AB = 48 mm, CD = 41 mm, $\delta=47^$.

a) Számítsa ki az ABC háromszög területét!

b) Számítással igazolja, hogy (egész milliméterre kerekítve) a háromszög BC oldalának hossza 60 mm!

c) Számítsa ki a háromszög B csúcsánál lévő belső szög nagyságát!

365. találat: Matematika középszintű érettségi, 2013. október, II. rész, 15. feladat
Témakör: *Halmazok (Venn-diagram, statisztika, logika) (Azonosító: mmk_201310_2r15f )

Egy végzős osztály diákjai projektmunka keretében különböző statisztikai felméréseket készítettek az iskola tanulóinak körében.

a) Éva 150 diákot kérdezett meg otthonuk felszereltségéről. Felméréséből kiderült, hogy a megkérdezettek közül kétszer annyian rendelkeznek mikrohullámú sütővel, mint mosogatógéppel. Azt is megtudta, hogy 63-an mindkét géppel, 9-en egyik géppel sem rendelkeznek. A megkérdezettek hány százalékának nincs otthon mikrohullámú sütője?

b) Jóska a saját felmérésében 200 diákot kérdezett meg arról, hogy hány számítógépük van a háztartásban. A válaszokat a következő táblázatban összesítette:

A számítógépek szá- ma a háztartásban	Gyakoriság
0	3
1	94
2	98
3	14

Jóska felmérése alapján töltse ki az alábbi táblázatot az egy háztartásban található számítógépek számáról!

A számítógépek számának átlaga

A számítógépek számának mediánja

A számítógépek számának módusza

c) Tamás a saját felmérése alapján a következőt állítja: Minden háztartásban van televízió. Az alábbi négy állítás közül válassza ki azt a kettőt, amely Tamás állításának tagadása!

A) Semelyik háztartásban nincs televízió.

B) Van olyan háztartás, ahol van televízió.

C) Van olyan háztartás, ahol nincs televízió.

D) Nem minden háztartásban van televízió.

366. találat: Matematika középszintű érettségi, 2013. október, II. rész, 16. feladat
Témakör: *Függvények (algebra, exponenciális, térgeometria, sorozat, mértani, logaritmus) (Azonosító: mmk_201310_2r16f )

A kólibaktérium (hengeres) pálcika alakú, hossza átlagosan 2 mikrométer $(2\cdot10^ m)$, átmérője 0,5 mikrométer $(5\cdot10^ m)$ .

a) Számítsa ki egy 2 mikrométer magas és 0,5 mikrométer átmérőjű forgáshenger térfogatát és felszínét! Számításainak eredményét m 3 -ben, illetve m 2 -ben, normálalakban adja meg!

Ideális laboratóriumi körülmények között a kólibaktériumok gyorsan és folyamatosan osztódnak, számuk 15 percenként megduplázódik. Egy tápoldat kezdetben megközelítőleg 3 millió kólibaktériumot tartalmaz.

b) Hány baktérium lesz a tápoldatban 1,5 óra elteltével?

A baktériumok számát a tápoldatban t perc elteltével a $B(t)=9000000 \cdot 2^>$ összefüggés adja meg.

c) Hány perc alatt éri el a kólibaktériumok száma a tápoldatban a 600 milliót? Válaszát egészre kerekítve adja meg!

367. találat: Matematika középszintű érettségi, 2013. október, II. rész, 17. feladat
Témakör: *Koordinátageometria (Thalesz) (Azonosító: mmk_201310_2r17f )

Adott a koordináta-rendszerben két pont: A(1; –3) és B(7; –1).

a) Írja fel az A és B pontokra illeszkedő e egyenes egyenletét!

b) Számítással igazolja, hogy az A és a B pont is illeszkedik az $x^2+y^2-6x-2y=10$ egyenletű k körre, és számítsa ki az AB húr hosszát!

Az f egyenesről tudjuk, hogy illeszkedik az A pontra és merőleges az AB szakaszra.

c) Számítsa ki a k kör és az f egyenes (A-tól különböző) metszéspontjának koordinátáit!

368. találat: Matematika középszintű érettségi, 2013. október, II. rész, 18. feladat
Témakör: *Valószínűségszámítás (kombinatorika) (Azonosító: mmk_201310_2r18f )

a) Egy memóriajáték 30 olyan egyforma méretű lapból áll, melyek egyik oldalán egy-egy egész szám áll az 1, 2, 3, … 14, 15 számok közül. Mindegyik szám pontosan két lapon szerepel. A lapok másik oldala (a hátoldala) teljesen azonos mintázatú. A 30 lapot összekeverjük. A játék kezdetén a lapokat az asztalra helyezzük egymás mellé, hátoldalukkal felfelé fordítva, így a számok nem látszanak. Számítsa ki annak a valószínűségét, hogy a játék kezdetén két lapot véletlenszerűen kiválasztva a lapokon álló számok megegyeznek!

b) Egy dominókészlet azonos méretű kövekből áll. Minden dominókő egyik oldala egy vonallal két részre van osztva. Az egyes részeken elhelyezett pöttyök száma 0-tól 6-ig bármi lehet. Minden lehetséges párosításnak léteznie kell, de két egyforma kő nem lehet egy készletben. Az ábrán két kő látható: a 4-4-es és a 0-5-ös (vagy 5-0-ás). Hány kőből áll egy dominókészlet?

c) A „Ki nevet a végén?” nevű társasjátékban egy játékos akkor indulhat el a pályán, amikor egy szabályos dobókockával 6-ost dob. Számítsa ki annak a valószínűségét, hogy valaki pontosan a harmadik dobására indulhat el a pályán!

369. találat: Matematika középszintű érettségi, 2014. május, I. rész, 1. feladat
Témakör: *Halmazok ( metszet, különbség) (Azonosító: mmk_201405_1r01f )

Legyen A halmaz a 8-nál nem nagyobb pozitív egész számok halmaza, B pedig a 3-mal osztható egyjegyű pozitív egész számok halmaza. Elemeinek felsorolásával adja meg az A, a B, az $A \cap B$ és az $A \setminus B$ halmazt!

370. találat: Matematika középszintű érettségi, 2014. május, I. rész, 2. feladat
Témakör: *Algebra ( százalék) (Azonosító: mmk_201405_1r02f )

Egy konzerv tömege a konzervdobozzal együtt 750 gramm. A konzervdoboz tömege a teljes tömeg $ 12\%$-a. Hány gramm a konzerv tartalma?

371. találat: Matematika középszintű érettségi, 2014. május, I. rész, 3. feladat
Témakör: *Algebra ( másodfokú) (Azonosító: mmk_201405_1r03f )

Oldja meg a következő egyenletet a valós számok halmazán:$(x-3)^2+2x=14$. Válaszát indokolja!

372. találat: Matematika középszintű érettségi, 2014. május, I. rész, 4. feladat
Témakör: *Függvények ( másodfokú, lineáris) (Azonosító: mmk_201405_1r04f )

Válassza ki az f függvény hozzárendelési szabályát az A, B, C, D lehetőségek közül úgy, hogy az megfeleljen az alábbi értéktáblázatnak:

x	-2	0	2
f(x)	-4	0	-4

$\textbf f(x)=2x \qquad \textbf f(x)=x^2 \qquad \textbf f(x)=-2x \qquad \textbf f(x)=-x^2 $

373. találat: Matematika középszintű érettségi, 2014. május, I. rész, 5. feladat
Témakör: *Halmazok (Azonosító: mmk_201405_1r05f )

Egy osztályban 25-en tanulnak angolul, 17-en tanulnak németül. E két nyelv közül legalább az egyiket mindenki tanulja. Hányan tanulják mindkét nyelvet, ha az osztály létszáma 30?

374. találat: Matematika középszintű érettségi, 2014. május, I. rész, 6. feladat
Témakör: *Algebra ( százalék) (Azonosító: mmk_201405_1r06f )

Egy termék árát az egyik hónapban $ 20\%$-kal, majd a következő hónapban újabb $ 20\%$-kal megemelték. A két áremelés együttesen hány százalékos áremelésnek felel meg? Válaszát indokolja!

375. találat: Matematika középszintű érettségi, 2014. május, I. rész, 7. feladat
Témakör: *Számelmélet ( oszthatóság) (Azonosító: mmk_201405_1r07f )

Melyik számjegy állhat a $\overline$ ötjegyű számban az X helyén, ha a szám osztható 3-mal? Válaszát indokolja!

376. találat: Matematika középszintű érettségi, 2014. május, I. rész, 8. feladat
Témakör: *Függvények ( abszolútérték) (Azonosító: mmk_201405_1r08f )

Az ábrán a [–1; 5] intervallumon értelmezett függvény grafikonja látható. Válassza ki a felsoroltakból a függvény hozzárendelési szabályát!

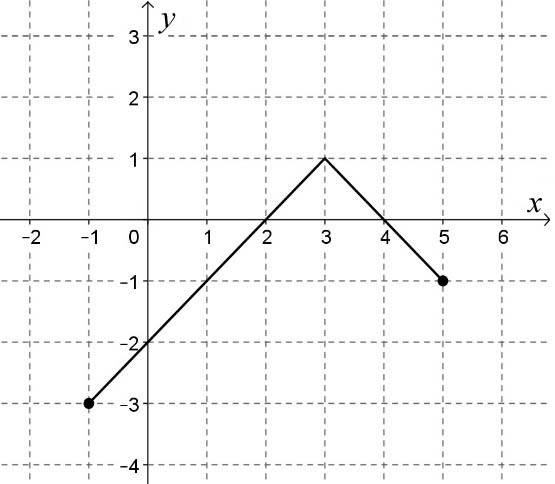
377. találat: Matematika középszintű érettségi, 2014. május, I. rész, 9. feladat
Témakör: *Algebra ( logaritmus) (Azonosító: mmk_201405_1r09f )

Adja meg az x értékét, ha $\log_2(x+1)=5$ .

378. találat: Matematika középszintű érettségi, 2014. május, I. rész, 10. feladat
Témakör: *Kombinatorika ( gráfok) (Azonosító: mmk_201405_1r10f )

Egy irodai számítógép-hálózat hat gépből áll. Mindegyik gép ezek közül három másikkal van közvetlenül összekötve. Rajzoljon egy olyan gráfot, amely ezt a hálózatot szemlélteti!

379. találat: Matematika középszintű érettségi, 2014. május, I. rész, 11. feladat
Témakör: *Geometria ( Thalesz-tétel, Pitagorasz-tétel) (Azonosító: mmk_201405_1r11f )

Egy téglalap szomszédos oldalainak hossza 4,2 cm és 5,6 cm. Mekkora a téglalap körülírt körének sugara? Válaszát indokolja!

380. találat: Matematika középszintű érettségi, 2014. május, I. rész, 12. feladat
Témakör: *Valószínűségszámítás (Azonosító: mmk_201405_1r12f )

Egy kalapban 3 piros, 4 kék és 5 zöld golyó van. Találomra kihúzunk a kalapból egy golyót. Adja meg annak valószínűségét, hogy a kihúzott golyó nem piros!

381. találat: Matematika középszintű érettségi, 2014. október, I. rész, 1. feladat
Témakör: *Koordinátageometria (Azonosító: mmk_201410_1r01f )

Írja fel annak az egyenesnek az egyenletét, amely áthalad az (1; –3) ponton, és egyik normálvektora a (8; 1) vektor!

382. találat: Matematika középszintű érettségi, 2014. október, I. rész, 2. feladat
Témakör: *Algebra (polinom, azonosság) (Azonosító: mmk_201410_1r02f )

Végezze el a következő műveleteket, és vonja össze az egynemű kifejezéseket! A számítás menetét részletezze!

383. találat: Matematika középszintű érettségi, 2014. október, I. rész, 3. feladat
Témakör: *Függvény (másodfokú) (Azonosító: mmk_201410_1r03f )

Adott a valós számok halmazán értelmezett $x\mapsto -(x-5)^2+4$ függvény. Melyik ábrán látható e függvény grafikonjának egy részlete?

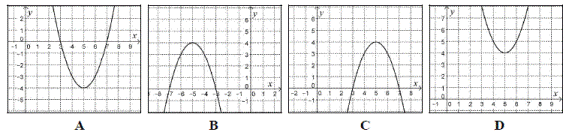
384. találat: Matematika középszintű érettségi, 2014. október, I. rész, 4. feladat
Témakör: *Algebra (egyenlet, abszolútérték) (Azonosító: mmk_201410_1r04f )

Adja meg az alábbi egyenlet megoldásait a valós számok halmazán!

385. találat: Matematika középszintű érettségi, 2014. október, I. rész, 5. feladat
Témakör: *Algebra (logaritmus, értelmezési tartomány) (Azonosító: mmk_201410_1r05f )

a) Mely valós számokra értelmezhető a$ \log_2(3-x)$kifejezés?
b) Oldja meg a valós számok halmazán az alábbi egyenletet! $ \log_2(3-x)=0$

386. találat: Matematika középszintű érettségi, 2014. október, I. rész, 6. feladat
Témakör: *Valószínűségszámítás ( számelmélet, oszthatóság) (Azonosító: mmk_201410_1r06f )

Az első 100 pozitív egész szám közül véletlenszerűen kiválasztunk egyet. Adja meg annak a valószínűségét, hogy a kiválasztott szám osztható 5-tel!

387. találat: Matematika középszintű érettségi, 2014. október, I. rész, 7. feladat
Témakör: *Algebra ( trigonometria, trigonometrikus egyenlet) (Azonosító: mmk_201410_1r07f )

Adja meg a következő egyenlet $[0; 2\pi]$ intervallumba eső megoldásának pontos értékét! $ \sin x= -1$

388. találat: Matematika középszintű érettségi, 2014. október, I. rész, 8. feladat
Témakör: *Függvények ( trigonometrikus függvény, trigonometria) (Azonosító: mmk_201410_1r08f )

Határozza meg a valós számok halmazán értelmezett $ x\mapsto 1+ \cos x$ függvény értékkészletét!

389. találat: Matematika középszintű érettségi, 2014. október, I. rész, 9. feladat
Témakör: *Koordinátageometria (Azonosító: mmk_201410_1r09f )

Egy kör érinti az y tengelyt. A kör középpontja a K(–2; 3) pont. Adja meg a kör sugarát, és írja fel az egyenletét!

390. találat: Matematika középszintű érettségi, 2014. október, I. rész, 10. feladat
Témakör: *Függvények ( másodfokú, értékkészlet, parabola) (Azonosító: mmk_201410_1r10f )

Az ábrán látható függvény értelmezési tartománya a [–2; 3] intervallum, két zérushelye –1 és 2. Az értelmezési tartományának mely részhalmazán vesz fel a függvény pozitív értéket?

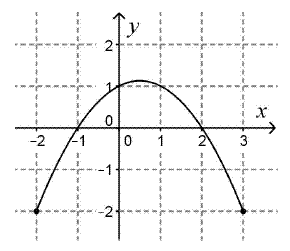
391. találat: Matematika középszintű érettségi, 2014. október, I. rész, 11. feladat
Témakör: *Algebra ( lineáris egyenletrendszer, egyenlő együtthatók) (Azonosító: mmk_201410_1r11f )

Oldja meg az alábbi egyenletrendszert a valós számpárok halmazán!

392. találat: Matematika középszintű érettségi, 2014. október, I. rész, 12. feladat
Témakör: *Algebra ( törtkitevő, hatvány, számelmélet, oszthatóság, logika,) (Azonosító: mmk_201410_1r12f )

Adja meg az alábbi állítások logikai értékét (igaz vagy hamis)!
A: Minden valós szám abszolút értéke pozitív.
B: $ 16^>=2$
C: Ha egy szám osztható 6-tal és 9-cel, akkor biztosan osztható 54-gyel is.

393. találat: Matematika középszintű érettségi, 2014. október, II. rész, 13. feladat
Témakör: *Halmazok (Venn-diagram,) (Azonosító: mmk_201410_2r13f )

Egy közvélemény-kutató intézet azt a feladatot kapta, hogy két alkalommal – fél év különbséggel – mérje fel a TV-ben látható három filmsorozat nézettségi adatait.

Az ábrán látható kérdőíven a válaszoló vagy azt jelölhette be, hogy az A, B és C sorozatok közül melyiket nézi (akár többet is meg lehetett jelölni), vagy azt, hogy egyiket sem nézi.

Az első felméréskor kapott 600 kérdőív jelöléseit összesítve megállapították, hogy az A sorozat összesen 90 jelölést kapott, a B sorozat összesen 290-et, a C sorozat pedig összesen 230-at. Érdekes módon olyan válaszadó nem volt, aki pontosan két sorozatot nézett volna, viszont 55-en mindhárom sorozatot bejelölték.

a) A válaszolók hány százaléka nézte az A sorozatot?

b) Hány válaszoló nem nézte egyik sorozatot sem?

A második felmérés után kiválogatták azokat a kérdőíveket, amelyeken valamelyik sorozat meg volt jelölve. Ezeken a három sorozat nézettségére összesen 576 jelölés érkezett. Az adatok feldolgozói minden jelölést megszámoltak, és a végeredményről az itt látható kördiagramot készítették. A második felmérés után kiválogatták azokat a kérdőíveket, amelyeken valamelyik sorozat meg volt jelölve. Ezeken a három sorozat nézettségére összesen 576 jelölés érkezett. Az adatok feldolgozói minden jelölést megszámoltak, és a végeredményről az itt látható kördiagramot készítették.

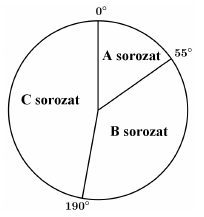
c) Számítsa ki, hogy az egyes sorozatok nézettségére hány jelölés érkezett!

394. találat: Matematika középszintű érettségi, 2014. október, II. rész, 14. feladat
Témakör: *Algebra (térgeometria, hasonlóság, ) (Azonosító: mmk_201410_2r14f )

Egy család személyautóval Budapestről Keszthelyre utazott. Útközben lakott területen belül, országúton és autópályán is haladtak. Az utazással és az autóval kapcsolatos adatokat a következő táblázat tartalmazza:

a) Mennyi ideig tartott az utazás?

b) Hány liter ezen az utazáson az autó 100 km-re eső átlagfogyasztása? Válaszát egy tizedesjegyre kerekítve adja meg!

Útközben elfogyott az autóból a benzin. A legközelebbi benzinkútnál kétféle benzineskannát lehet kapni. A nagyobbra rá van írva, hogy 20 literes, a kisebbre nincs ráírva semmi. A két kanna (matematikai értelemben) hasonló, a nagyobb kanna magassága éppen kétszerese a kisebb kanna magasságának.

c) Hány literes a kisebb kanna?

395. találat: Matematika középszintű érettségi, 2014. október, II. rész, 15. feladat
Témakör: *Térgeometria (geometria, Pitagorasz-tétel, koszinusztétel,) (Azonosító: mmk_201410_2r15f )

Egy téglatest alakú akvárium egy csúcsból kiinduló élei 30 cm, 40 cm, illetve 50 cm hosszúak.

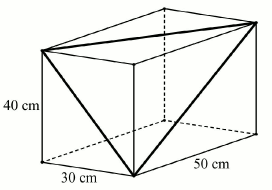
a) Hány literes ez az akvárium? (A számolás során tekintsen el az oldallapok vastagságától!)

Tekintsük azt a háromszöget, amelynek oldalait az ábrán látható téglatest három különböző hosszúságú lapátlója alkotja.

b) Mekkora ennek a háromszögnek a legkisebb szöge? Válaszát fokban, egészre kerekítve adja meg!

396. találat: Matematika középszintű érettségi, 2014. október, II. rész, 16. feladat
Témakör: *Sorozatok ( másodfokú) (Azonosító: mmk_201410_2r16f )

Egy számtani sorozat első tagja 56, differenciája –4.
a) Adja meg a sorozat első 25 tagjának összegét!
b) Számítsa ki az n értékét és a sorozat n-edik tagját, ha az első n tag összege 408.
Egy mértani sorozat első tagja 10 25 , hányadosa 0,01.
c) Hányadik tagja ennek a sorozatnak a 100 000?

397. találat: Matematika középszintű érettségi, 2014. október, II. rész, 17. feladat
Témakör: *Kombinatorika (térgeometria, kúp, kombináció, variáció) (Azonosító: mmk_201410_2r17f )

A biliárdjáték megkezdésekor az asztalon 15 darab azonos méretű, különböző színezésű biliárdgolyót helyezünk el háromszög alakban úgy, hogy az első sorban 5 golyó legyen, a másodikban 4, a következőkben pedig 3, 2, illetve 1 golyó. (A golyók elhelyezésére vonatkozó egyéb szabályoktól tekintsünk el.)

a) Hányféleképpen lehet kiválasztani a 15-ből azt az 5 golyót, amelyet majd az első sorban helyezünk el? (Az 5 golyó sorrendjét nem vesszük figyelembe.)

b) Hányféle különböző módon lehet az első két sort kirakni, ha a 9 golyó sorrendjét is figyelembe vesszük?

Egy biliárdasztal játékterülete téglalap alakú, mérete 194 cm × 97 cm. A játékterület középpontja felett 85 cm-rel egy olyan (pontszerűnek tekinthető) lámpa van, amely fénykúpjának a nyílásszöge 100°.

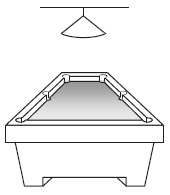
c) Számítással állapítsa meg, hogy a lámpa megvilágítja-e a játékterület minden pontját!

398. találat: Matematika középszintű érettségi, 2014. október, II. rész, 18. feladat
Témakör: *Kombinatorika (gráfok, statisztika, binomiális eloszlás, visszatevéses mintavétel) (Azonosító: mmk_201410_2r18f )

Egy focicsapat 11 játékosa megérkezik az edzésre, néhányan kezet fognak egymással. (Két játékos között legfeljebb egy kézfogás történik.) Az edző felírta, hogy ki hányszor fogott kezet, és a következő számokat kapta: 0; 1; 2; 2; 2; 5; 0; 0; 4; 4; 2.

a) Ábrázolja a kézfogásoknak egy lehetséges gráfját, ahol a pontok a játékosokat jelölik, és két pont között akkor van él, ha az illetők kezet fogtak az edzés előtt!

b) Hány kézfogás történt összesen?

Egy másik alkalommal az edző által feljegyzett 11 nemnegatív egész számról a következőket állapítottuk meg: a számok egyetlen módusza 2, mediánja 3, átlaga 4, terjedelme pedig 5 volt.

c) Adjon meg a fenti feltételeknek megfelelő 11 nemnegatív egész számot!

Az edzésen a játékosok a tizenegyesrúgást gyakorolják. Az egyik játékos 0,9 valószínűséggel lövi be a tizenegyest.

d) Mennyi a valószínűsége annak, hogy három rúgásból legalább egyszer betalál? A valószínűség pontos értékét adja meg!

399. találat: Matematika középszintű érettségi, 2015. május, I. rész, 1. feladat
Témakör: *Algebra (szorzattá alakítás, algebrai tört) (Azonosító: mmk_201505_1r01f )

Egyszerűsítse az $\dfrac$ törtet, ha $a\neq -1$.

400. találat: Matematika középszintű érettségi, 2015. május, I. rész, 2. feladat
Témakör: *Számelmélet (oszthatóság, oszthatósági szabály) (Azonosító: mmk_201505_1r02f )

Milyen számjegy állhat az X helyén, ha a négyjegyű $\overline$ szám 6-tal osztható?