Matematika 5. osztály

Logaritmikus egyenletek: szöveges feladatok. 115. A 226-os tömegszámú rádium izotóp 36,2 %-a 1050 év alatt bomlik el. Mennyi a felezési ideje?

Matematika felmérő feladatlapok 5. osztály

A Matematika felmérő feladatlapok 5. osztály füzetben lévő feladatlapok ehhez nyújtanak segítséget. Az egyes témakörökben szereplő feladatok megfelelnek a legújabb Nemzeti Alaptanterv 5. osztályos matematika követelményeinek, lefedik a tananyag egészét. A gyakorlófüzetben 8 témakör található, két-két feladatsorral, ami 6-7 feladatot tartalmaz. A felmérőfüzet végén rejtvényes feladatok találhatók, amelyek a kreatív gondolkodást fejlesztik. Minden feladat pontozással van ellátva. A feladatok értékelése során a tanulók visszajelzést kapnak az elsajátított tudásukról, az esetleges hiányosságukról.

Leírás

Amikor egy-egy tantárgy – így például a matematika – egyes témakörei végén nagyobb súlyú számonkérés történik az iskolában, arra érdemes alaposan felkészülni.
A Matematika felmérő feladatlapok 5. osztály füzetben lévő feladatlapok ehhez nyújtanak segítséget. Az egyes témakörökben szereplő feladatok megfelelnek a legújabb Nemzeti Alaptanterv 5. osztályos matematika követelményeinek, lefedik a tananyag egészét. A gyakorlófüzetben 8 témakör található, két-két feladatsorral, ami 6-7 feladatot tartalmaz. A felmérőfüzet végén rejtvényes feladatok találhatók, amelyek a kreatív gondolkodást fejlesztik. Minden feladat pontozással van ellátva. A feladatok értékelése során a tanulók visszajelzést kapnak az elsajátított tudásukról, az esetleges hiányosságukról.

Matematika 5. osztály

Írásbeli összeadás-kivonás

Többjegyű számok írásbeli összeadása, kivonása. Négyjegyű számok írásbeli összeadását és kivonását a kisebb számokhoz hasonlóan végezzük. Ez könnyebb, mint a fejben számolás, csak pontosnak kell lenned. Elvégzünk néhány műveletet, más műveletekben a hiányzó számjegyeket kell pótolnod, majd szöveges feladatokkal is gyakorlunk.

PÓTOLD A HIÁNYOSSÁGAIDAT

5.-es pótold a hiányosságaidat

Útmutató

Ha vannak esetleges korábbi hiányosságaid, akkor először azokat pótold, hogy ne okozzon úja és újra gondot az új tananyag megértésében.

ITT TARTOK A TANKÖNYVBEN

5. osztályos

5. osztályos “A” tankönyv

Útmutató

Megmutatjuk, hogy a tankönyv egyes fejezeteihez melyik Matek Oázis leckék kapcsolódnak. (Továbbra is javasoljuk, hogy a Matek Oázis leckéket fejezetenként az első leckétől az utolsóig sorban vedd át, és közben gondolkozz, válaszolj a kérdésekre.).

5. osztályos

5. osztályos “B” tankönyv

Útmutató

SZÜLŐKNEK

A hiányosságok pótlása

Útmutató

Ha vannak elmaradásai gyermekednek az előző évekből, azokat gyorsan és könnyen behozhatja a “Pótold a hiányosságaidat” modul videóival. Nézd meg, hogyan! A legfontosabb anyagrészeket válogattuk ki az előző évfolyamok tananyagából.

5 lépéses Matek Oázis-módszer

Útmutató

Megmutatjuk, hogyan működik az 5 lépéses Matek Oázis módszer, amellyel gyermeked is valódi tudáshoz és sikerélményhez juthat matekból.

Hogyan használd a Matek Oázist?

Útmutató

Hogyan érdemes használni a matek videókat, hogy a legjobb eredményt érjétek el matekból szórakoztató módon tanulva? Velünk nem csak a matekot gyakorolhatod, hanem csillagokat, érmeket, kupákat is gyűjthetsz. Lépésről lépésre elmondjuk, hogyan kezdj hozzá, és hogyan folytasd. Célunk, hogy mindent érts, és a feladatokat is meg tudd oldani. Akár 4-szer gyorsabban haladhatsz, mint a suliban, mivel interaktívan, az alapoktól kezdve és szemléltetve magyarázunk.

A Tanulási naplóról szülőknek

Útmutató

A Tanulási naplóból nyomon követheted gyermeked haladását a matek videókkal. Megmutatjuk, hol találod, és mit láthatsz belőle: mikor és mennyit foglalkozott a tananyaggal, milyen eredményt ért el, milyen sorrendben nyitotta meg a videókat.

HOL IS KEZDJEM?

4 alfejezet / 8 tananyag

01. A hét legnépszerűbb videója (hétfőnként cseréljük)

Írásbeli összeadás-kivonás

02. PÓTOLD A HIÁNYOSSÁGAIDAT

5.-es pótold a hiányosságaidat

Ha vannak esetleges korábbi hiányosságaid, akkor először azokat pótold, hogy ne okozzon úja és újra gondot az új tananyag megértésében.

03. ITT TARTOK A TANKÖNYVBEN

5. osztályos “A” tankönyv

04. SZÜLŐKNEK

A hiányosságok pótlása

Megmutatjuk, hogyan működik az 5 lépéses Matek Oázis módszer, amellyel gyermeked is valódi tudáshoz és sikerélményhez juthat matekból.

Műveletek számokkal

Természetes számok, alapműveletek

Csillagaim: 0 /15

Helyiértékek

Tananyag

Tízes számrendszer. Megfigyeljük, hogyan változik meg a számok értéke, ha egymás mellé írjuk őket. Nem mindegy, melyik helyen áll. Ennek alapja a tízes számrendszer, és a helyiértékek. Megnézzük, milyen szerepe van a nullának. Szorzás és osztás 10-zel, 100-zal, 1000-rel. A szám végére hozzáteszünk annyi 0-t, amennyi a szorzóban van, illetve elveszünk annyi 0-t, amennyi az osztóban van. Kerekítés. Kerekítünk tízesre, százasra. Számegyenes. Megkeressük a számok helyét a számegyenesen.

Nagy számok

Tananyag

Helyiérték táblázat. Bővítjük a helyiérték táblázatot a milliárd, billió és trillió fogalmával. Megtanuljuk a nagyon nagy, sok számjegyből álló számokat kimondani, leírni. Műveletek nagy számokkal. Gyakoroljuk a műveletvégzést, kerekítést is.

Alapműveletek

Tananyag

Átismételjük a természetes számokról tanultakat. Mik azok a természetes számok? Műveletek természetes számokkal. Összeadás, kivonás, szorzás, osztás fejben és írásban természetes számokkal. Műveletvégzés sorrendje. Kezdjük a zárójelben lévő műveletekkel, aztán először a szorzás, osztás és végül az összeadás, kivonás.

Számolj fejben!

Teszt

TESZT! Tornáztasd az agytekervényeidet! Gyakorold a fejben számolást, az összeadást, kivonást, szorzást, osztást nagyobb számokkal. Oldd meg a feladatokat önállóan! Kiértékelés után levezetjük a megoldást lépésről-lépésre.

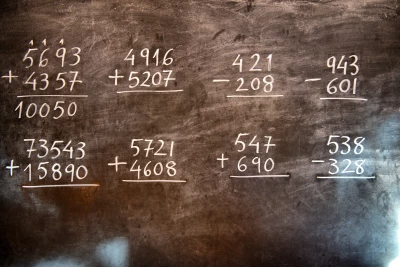
Műveleti sorrend

Teszt

TESZT! Gyakorold a műveletvégzés sorrendjét! Jó sok számolás vár, de kitartás, mert gyakorlás teszi a mestert. Oldd meg a feladatokat önállóan! Kiértékelés után levezetjük a megoldást lépésről-lépésre. Kiderül, valóban elsajátítottad-e a tananyagot.

Fejszámolás, alapműveletek gyakorlása – játékok

Csillagaim: 0 /15

Egyjegyű szorzás/osztás

Játék

JÁTÉK! Játszva tanuld a szorzást, osztást az egyjegyű pozitív egész számok körében! Kezdő, haladó és profi szinten is gyakorolhatsz, majd versenyezhetsz a többiekkel.

Kétjegyű szorzás

Játék

JÁTÉK! Játszva mélyítsd el tudásod a szorzás terén 100-nál kisebb eredményt adó pozitív egész számok körében. Kezdő, haladó és profi szinten is gyakorolhatsz, majd versenyezhetsz is a többiekkel.

Kétjegyűek osztása

Játék

JÁTÉK! Osztás 100-nál kisebb pozitív egész számok körében.

Kétjegyű összeadás

Játék

JÁTÉK! Játszva mélyítsd el tudásod az összeadás terén a 100-nál kisebb eredményt adó pozitív egész számok körében. Kezdő, haladó és profi szinten is gyakorolhatsz, majd versenyezhetsz is a többiekkel.

Kétjegyű kivonás

Játék

JÁTÉK! Játszva mélyítsd el a tudásod a kivonás terén a 100-nál kisebb eredményt adó pozitív egész számok körében. Kezdő, haladó és profi szinten is gyakorolhatsz, majd versenyezhetsz is a többiekkel.

Írásbeli műveletek gyakorlása

Csillagaim: 0 /18

Írásbeli összeadás-kivonás

Tananyag

Írásbeli szorzás kétjegyű számokkal

Tananyag

Írásbeli szorzás kétjegyű számokkal. Egyjegyűekkel már megtanultál írásban szorozni, nézzük meg, hogyan megy ez kétjegyű számokkal! Nagyon fontos, hogy az írásbeli műveletek jól menjenek, hisz a legtöbb matek példában szükséged lesz az ilyen számításokra. Sok példával, szöveges feladatokkal gyakorlunk. 1-es a szorzóban. Ha 1-es számjegy van a szorzóban, akkor egyszerűbben is leírhatjuk az írásbeli szorzást, ezt is megmutatjuk.

Maradékos osztás

Tananyag

Gyakoroljuk a maradékos osztásokat is írásban! Az írásbeli osztásnál is előfordul, hogy az eredmény mellett még maradék is van. Sok példán keresztül gyakorlunk és szöveges feladatokat is oldunk meg együtt a témában. A videó végére egyedül is menni fog, meglátod.

Osztás kétjegyű osztóval

Tananyag

Hogyan kell kétjegyű számmal osztani? Ezen a videón megmutatjuk, hogyan is kell kétjegyű számmal osztani . Ehhez jól kell tudnod az egyszerűbb osztásokat. Fontos szerepe lesz a helyiértéknek. A maradékos osztást is gyakoroljuk.

Osztás többjegyű osztóval

Tananyag

Hogyan kell többjegyű osztóval osztani? Ha kétjegyűvel már biztonsággal tudsz osztani, csak egy kis lépés a nagyobb számmal való osztás. Lépésről-lépésre haladva mutatjuk be ezt is, és be is gyakoroljuk számolási és szöveges feladatokban is. A becslés is a segítségünkre lesz és megmutatjuk azt is, hogyan találd meg a becsült értékeket.

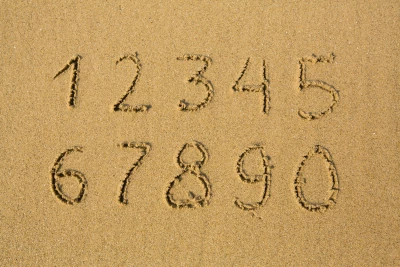
Írásbeli számolás

Teszt

TESZT! Gyakorold az írásbeli összeadást, kivonást, szorzást és osztást! Oldd meg a feladatokat önállóan! Kiértékelés után levezetjük a megoldást lépésről-lépésre. Kiderül, valóban elsajátítottad-e a tananyagot.

Római számok

Tananyag

A római számokkal ismerkedünk ezen a videón. Tudod pl. mennyi ez a szám: MDCCCLXXXVIII ? Megtanuljuk leolvasni és leírni ezeket a több, mint kétezer éves, de még ma is használatos számokat.

Római számok 100-ig

Játék

JÁTÉK! Mivel egyenlők az elsettenkedő római számok Kezdd egy kis gyakorlással :), azután irány a verseny, és nyerd meg “A fejben számolás Mestere” díjat! A verseny pontozása: jó válaszok: 2 pont rossz válasz: -1 pont elszalasztás: élet vesztés és -2 pont Teljesített szintek után járó pontok: 10, 15, 20 és 25 pont

Római számok gyakorlása

Játék

JÁTÉK! Gyakorold a római számok írását! Melyik betű (vagyis római szám) hiányzik a számból? Kattints arra, ami a kérdőjel helyére illik!

Műveletek számokkal

4 alfejezet / 19 tananyag

01. Természetes számok, alapműveletek

02. Fejszámolás, alapműveletek gyakorlása – játékok

Egyjegyű szorzás/osztás

JÁTÉK! Játszva tanuld a szorzást, osztást az egyjegyű pozitív egész számok körében! Kezdő, haladó és profi szinten is gyakorolhatsz, majd versenyezhetsz a többiekkel.

JÁTÉK! Osztás 100-nál kisebb pozitív egész számok körében.

03. Írásbeli műveletek gyakorlása

Írásbeli összeadás-kivonás

04. Római számok

JÁTÉK! Gyakorold a római számok írását! Melyik betű (vagyis római szám) hiányzik a számból? Kattints arra, ami a kérdőjel helyére illik!

Matematika. felmérő feladatlapok 5. osztály MEGOLDÁSOK

2 1. Természetes számok 1. megoldás Összedás, kivonás, szorzás, kerekítés, mértékegységek 1. ) 9400; 5027; Becslés: = Összegük: b) ; Becslés: = 9000 Különbségük: 8529 Ellenőrzés: = c) 87; 206 Becslés: = Szorztuk: x ) Tízezresre: Ezresre: Százsr: Tízesre: b) < m 8 dm = 218 dm = mm; m = 28 km = cm; 6500 dkg = 65 kg = g; 00 q = kg = 0 t; 5 h 40 min 15 s = s; 12 hét 5 np = 89 np = 216 h 5. Adtok felírás: 14 db/sor; 8 sor; 45 lád Terv: Egy ládábn 14 8 db = 112 db lm fér el. 45 ládábn db = 5040 db lm fér el. 2

3 6. Adtok felírás: 24 db muffin; 18 g/db; sütés után 2 g/db-bl kevesebb Terv: (18 2) 24 1 db muffin sütés utáni tömege: 18 g 2 g = 16 g. 24 db muffin sütés utáni tömege: g = 84 g. 2. Természetes számok 2. megoldás Összedás, kivonás, szorzás, kerekítés, mértékegységek 1. ) 8060; 42; Becslés: = Összegük: b) ; Becslés: = Különbségük: Ellenőrzés: = c) 291; 05 Becslés: = Szorztuk: x ) Tízezresre: Ezresre: Százsr: Tízesre: b) < 2 500

4 4. 2 km 80 dm = 2008 m = dm; 8100 cm = 810 dm = mm; 7000 kg = 7 t = 70 q; 000 dkg = 0 kg = g; 4 h 20 min 48 s = s; 14 hét 2 np = 100 np = 2400 h 5. Adtok felírás: 12 kg 65 dkg = 1265 dkg; 1 kg 80 dkg = 180 dkg Terv: Számolás: = 250 Válsz: 250 dkg = 2 kg 50 dkg lm vn két kosárbn összesen. 6. Adtok felírás: 80 Ft/np; 5 np; 220 Ft. Eredetileg volt 540 Ft. Terv: 540 ( ) Számolás: = 1420 Válsz: 1420 Ft-j mrdt hét végére.. Természetes számok. megoldás Osztás, műveletsorok, rányosságok, összefüggések, grfikonok, soroztok, egyenletek 1. Becslés: 800 hánydos < 900 Osztás: : 65 = 864, mrdék: 44 Ellenőrzés: = ; = Műveleti sorrend: 1. zárójelbeli szorzás 2. összedás. osztás 4. szorzás 5. kivonás ( ) : = ( ) : = = 875 : = = = = = = literes 24 s ltt 24 : 8 =, zz 1 literes s ltt 15 literes? s ltt 15 s = 45 s ltt 4

5 4. 2 dl-es 28 db 8 dl-es, mi 4-szer nnyi, mint 2 dl-es. 28 db : 4 = 7 db-ot tud megtölteni. 5. ) Szbály: = b; b : = ; b : = b pont b) b Szbály: = 56; = 62; = 70 Azz 2-vel nő tgok közötti különbség. Sorozt: 50; 50; 52; 56; 62; 70; 80; 92 4 pont 7. Gondolt szám: x Műveletek: x Egyenlet: x = 1477 (H egyből felírj z egyenletet, kkor is jár.) Rákmódszer: x = ( ) : 17 x = 107 Ellenőrzés: = =

7 b) y x 6. Szbály: 52 + = 55; = 61; 61 + = 64 Azz tgokhoz felváltv -t, illetve 6-ot dunk hozzá. Sorozt: 4; 46; 52; 55; 61; 64; 70; 7 4 pont 7. Gondolt szám: x Műveletek: x : Egyenlet: x : = 75 (H egyből felírj z egyenletet, kkor is jár.) Rákmódszer: x = (75 52) 7 x = 1547 Ellenőrzés: 1547 : = = 75 7

8 5. Kerület, terület, felszín, térfogt 1. megoldás Síkidomok, sokszögek; négyzet, tégllp; kock, tégltest, négyzetes oszlop 1. Kerület: 24 hosszúságegység Terület: 17 területegység 2. Adtok: b = 50 mm = 5 cm b = 19 cm K =? T =? Számolás: K = 2 ( + b) T = b K = 2 (5 cm + 19 cm) T = 5 cm 19 cm K = 108 cm T = 665 cm 2. Adtok: K = 164 m T =? Számolás: K = 4 T = 164 m = 4 T = 41 m 41 m = 41 m T = 1681 m dm = cm = 260 dl m 2 = 6 h = dm cl = 800 dm = 8 hl 5. Adtok: = 5 cm V =? Számolás: V = V = 5 cm 5 cm 5 cm V = 125 cm = 125 ml víz fér bele. 6. Adtok: b c = 9 cm b = 5 cm c = 12 cm A =? V =? 8

9 Számolás: A = 2 ( b + c + b c) A = 2 ( 9 cm 5 cm + 9 cm 12 cm + 5 cm 12 cm) A = 426 cm 2 V = b c V = 9 cm 5 cm 12 cm V = 540 cm 7. Adtok: b c = 4 cm b = 9 cm c = 4 cm =, zz négyzetes oszlop A =? V =? Hiányzó lpok: 4 cm és 4 cm; 4 cm és 9 cm; vlmint 4 cm és 9 cm Számolás: A = b A = 2 4 cm 4 cm cm 9 cm A = 176 cm 2 V = b V = 4 cm 4 cm 9 cm V = 144 cm 9

10 6. Kerület, terület, felszín, térfogt 2. megoldás Síkidomok, sokszögek; négyzet, tégllp; kock, tégltest, négyzetes oszlop 1. Kerület: 24 hosszúságegység Terület: 14 területegység 2. Adtok: b = és fél dm = 5 cm K = 108 cm T =? Számolás: K = b T = b 108 cm = 2 5 cm + 2 b T = 5 cm 19 cm b = 19 cm T = 665 cm 2. Adtok: = 9 cm K =? T =? Számolás: K = 4 T = K = 4 9 cm T = 9 cm 9 cm K = 6 cm T = 81 cm m = 6000 dm = 60 hl 59 h = m 2 = dm ml = 50 dm = fél hl 5. Adtok: = 4 cm A =? Számolás: A = 6 A = 6 4 cm 4 cm A = 96 cm 2 = 9600 mm 2 6. Adtok: b c 10 = 9 cm b = 8 cm c = 6 cm A =? V =?

11 Számolás: A = 2 ( b + c + b c) A = 2 (9 cm 8 cm + 9 cm 6 cm + 8 cm 6 cm) A = 48 cm 2 V = b c V = 9 cm 8 cm 6 cm V = 42 cm 7. Adtok: b c = cm b = 8 cm c = cm =, zz négyzetes oszlop A =? V =? Hiányzó lpok: cm és cm; cm és 8 cm; vlmint cm és 8 cm 8 8 Számolás: A = b A = 2 cm cm + 4 cm 8 cm A = 114 cm 2 V = b V = cm cm 8 cm V = 72 cm 11

12 7. Egész számok 1. megoldás Ellentett, bszolút érték, műveletek, derékszögű koordinát-rendszer, egyenletek 1. Ellentettek: ( ) = ; (+ 2) = 2; (0) = 0 Abszolút értékek: = ; + 2 = 2; 0 = (H hibátln z ábrázolás, kkor ; h vn benne hib, kkor.) 2. ) 12 + ( 7) = 12 7 = 19 8 ( 11) = = (+ 9) = 15 9 = 6 (+ 2) (+ 17) = 2 17 = 6 (H rögtön végeredményt írt le, kkor is kpj meg ot.) b) 5 + ( 9) ( 7) = = 7 16 (+ 19) + ( 1) = = 16 (H rögtön végeredményt írt le, kkor is kpj meg ot.) c) ( 5) (+ 1) = ( 5) 1 = 65 ( 9) 12 = 108 ( 25) : (+ 5) = 25 : 5 = 5 ( 64) : 8 = 8. ) ( 7) (+ ) ( 16) + ( 42) : 7 = 21 ( 16) + ( 6) = = = = 11 b) ( 4) [2 + ( 18)] ( 4) : (+ 2) = 4 [5] + 4 : 2 = = : 2 = = = = 4. koordinát-rendszer tengelyekkel, nyilkkl 12

13 y A 4 2 B C 1 x 2 D 4 pont 5. b = ( 5) b = b = (b 5) : 6 pont < x 8 ( számokr, relációs jelekre) x = 11; 10; ; 7; 8 1

14 8. Egész számok 2. megoldás Ellentett, bszolút érték, műveletek, derékszögű koordinát-rendszer, egyenletek 1. Ellentettek: ( 5) = 5; (0) = 0; (+ ) = Abszolút értékek: 5 = 5; 0 = 0; + = (H hibátln z ábrázolás, kkor ; h vn benne hib, kkor.) 2. ) 9 ( 15) = = 24 (+ 21) (+ 8) = 21 8 = ( 1) = 18 1 = 1 14 (+ 7) = 14 7 = 7 (H rögtön végeredményt írt le, kkor is kpj meg ot.) b) 6 ( 14) + (+ 21) = = 29 ( 12) (+ 5) ( 11) = = 6 (H rögtön végeredményt írt le, kkor is kpj meg ot.) c) ( 2) (+ 2) = 46 ( 8) 16 = 128 ( 65) : (+ 5) = 65 : 5 = 1 ( 6) : 7 = 9. ) ( 56) : 8 + ( 9) (+ 4) ( 25) = 7 6 ( 25) = = = = 18 b) ( 4) : [ 22 + (+ 9)] ( 4) (+ ) = ( 4) : [17] ( 12) = = 2 ( 12) = = = = koordinát-rendszer tengelyekkel, nyilkkl 14

15 y 6 5 C 4 B A 2 x 4 D 5. b = 4 + ( 2) b = pont b = (b + 2) : 4 6 pont 6. 6 < x 12 ( számokr, relációs jelekre) x = 5; 4; ; 11; 12 15

16 9. A szögek mérése 1. megoldás Szögek, szögmérés, szögfjták, sokszögek szögei 1. α = 12 és tompszög β = 55 és hegyesszög γ = 250 és homorúszög δ = 90 és derékszög 2. α = = 210 ; 70 4 = 280 ; 70 5 = 50, zz -ml, 4-gyel vgy 5-tel kell megszorozni.. ) Lehet hegyesszög, pl = 50. Lehet derékszög, pl = 90. Lehet tompszög, pl = 150. b) Csk hegyesszög lehet, pl = 70. c) Csk tompszög lehet, pl = α = 6 ; β = 5 ; γ = 127 ; δ = 45 ; ε = 252 (Minden szög, kivéve z utolsót, mi.) 5. Kisebb szög: α Ngyobb szög: α 2 Összefüggés: α + α 2 = = 168 Megoldás: α = 56 Ngyobb szög: 56 2 = 112 Ellenőrzés: = α = 56 β = 112 (A szögek rjzolásánál ± 2 eltérést megengedünk.) 16

17 6. ) 5 perc ltt 0 -ot fordul. 25 perc ltt 5 0 = 150 -ot. b) 0 -ot 1 ór ltt fordul ot 210 : 0 = 7 ór ltt. c) 1 órkor 0 -ot. 4 órkor 4 0 = 120 -ot. 10. A szögek mérése 2. megoldás Szögek, szögmérés, szögfjták, sokszögek szögei 1. α = 76 és hegyesszög β = 195 és homorúszög γ = 90 és derékszög δ = 112 és tompszög 2. α = 5 5 = 105 ; 5 4 = 140 ; 5 5 = 175, zz -ml, 4-gyel vgy 5-tel kell megszorozni.. ) Lehet hegyesszög, pl = 70. Lehet derékszög, pl = 90. Lehet tompszög, pl = 100. b) Csk hegyesszög lehet, pl = 80. c) Csk homorúszög lehet, pl = α = 82 ; β = 8 ; γ = 4 ; δ = 258 ; ε = 8 (Minden szög, kivéve δ-t, mi.) 5. Kisebb szög: α Ngyobb szög: α Összefüggés: α + α = = 144 Megoldás: α = 6 Ngyobb szög: 6 = 108 Ellenőrzés: =

18 α = 6 β = 108 (A szögek rjzolásánál ± 2 eltérést megengedünk.) 6. ) 5 perc ltt 0 -ot fordul. 45 perc ltt 9 0 = 270 -ot. b) 0 -ot 1 ór ltt fordul ot 240 : 0 = 8 ór ltt. c) 1 órkor 0 -ot. 5 órkor 5 0 = 150 -ot. 11. Törtek 1. megoldás Értelmezés, összehsonlítás, egyszerűsítés, bővítés, műveletek törtekkel 1. ) 4 16 része, zz 1 4 része. b) 7 db 16-ból, zz 9 db színezetlen, mi 9 16 rész = 6 12 ; 9 12 ; 7 12 ; 2 = 8 12 ; 1 6 = 2 12 ; pont

19 4. 5 h = 50 min, mert 60 : 6 5 = 50 6 m = 150 cm, mert 100 : 2 = egyenesszög = 180 = m 2 = 10 ár = 1 h ) = = b) = = 1 10 c) 4 5 = 15 4 d) 4 5 : = 4 15 e) 12 7 : 4 = 7 f) ( ( : 2 + ( ( = ( ( : 2 + ( ( = = 17 6 : = = = = = = Adtok: első np: 8 rész második np: 8 : 2 = 16 rész hrmdik np: 1 4 rész Terv: 1 ( Számolás: 1 ( ( ( = 1 ( ( = = = = 16 Válsz: Az utunk 16 része mrd z utolsó npr. 1 pont 19

20 12. Törtek 2. megoldás Értelmezés, összehsonlítás, egyszerűsítés, bővítés, műveletek törtekkel 1. ) 6 16 része, zz 8 része. b) 7 db 16-ból, zz 9 db színezetlen, mi 9 16 rész = 8 16 ; 16 ; 1 4 = 4 16 ; 7 8 = ; 2 16 ; pont m = km = km min = 40 s, mert 60 : 2 = 40 2 hl = 40 l, mert 100 : 5 2 = derékszög = 90 = ) = = 7 12 b) = = 1 6 c) 4 5 = 20 d) 8 5 : 2 = 4 5 e) 5 : 2 = 10 20

21 ( ( f) ( ( : 2 = ( ( ( : 2 = ( = : 2 = = = = = = = = 8 6. Adtok: első ór: 1 8 rész második ór: 1 8 = 8 rész hrmdik ór: 16 rész Terv: 1 ( Számolás: 1 ( ( = 1 ( ( ( = = = = 5 16 Válsz: Julis néni árujánk z 5 16 része mrd meg. 1 pont 21

22 1. Ponthlmzok 1. megoldás Merőlegesség, párhuzmosság, kör, gömb, szkszfelező merőleges, háromszög és tégllp szerkesztése 1. ) m m merőleges egyenes megrjzolás A keresett távolság z FT szksz hossz. F FT = 40 mm T b) FT = 40 mm távolság vlóságbn: 40 mm 4000 = = mm = = 160 m 2. P r R r = 2 cm R = 4 cm 2 cm sugrú kör belső kör kékkel áthúzv 4 cm sugrú kör külső kör kékkel áthúzv körgyűrű kiszínezve körgyűrű megnevezése. Vázlt: C b = 4 cm = 40 mm b = 5 mm c = fél dm = 50 mm A c B 22

23 Szerkesztés menete: 1. A kezdőpontú félegyenesre c szksz felvétele A, B pontok; 2. A középpontú, b sugrú körív;. B középpontú, sugrú körív; 4. két körív metszéspontj C csúcs. (Jó úgy is, h szerkesztésben megszámozz lépéseket.) Szerkesztés: C b A c B 4 pont Kerület: K = + b + c K = 40 mm + 5 mm + 50 mm K = 125 mm = 12 és fél cm 4. ) 1; 2; 5; 6; 7 2,5 pont b) 2; ; 6; 7 c) 1; 6 d) 1; 6; 8 1,5 pont e) 1; 2; 5; 6 5. ) (Minden helyes szám 0,5 pont. H rossz is vn, kkor drbonként 0,5 pont levonás, de z összpontszám negtív nem lehet.) b c b; c; b c 2

24 b) b c d d ; d b; d c 6. 6 cm hosszúságú szksz körívek megrjzolás körzővel felezőmerőleges megrjzolás A B 24

25 14. Ponthlmzok 2. megoldás Merőlegesség, párhuzmosság, kör, gömb, szkszfelező merőleges, háromszög és tégllp szerkesztése 1. ) m m merőleges egyenes megrjzolás A keresett távolság HT szksz hossz. HT = 8 mm H f T b) HT = 8 mm távolság vlóságbn: 8 mm 6000 = = mm = = 228 m 2. f cm cm cm távolságr egy párhuzmos egyenes ez z egyenes kékkel áthúzv cm távolságr egy másik párhuzmos egyenes ez z egyenes kékkel áthúzv párhuzmos egyenespár közti rész kékkel színezve párhuzmos egyenespár megnevezése. Vázlt: C b = cm = 0 mm b = 5 mm c = fél dm = 50 mm A c B 25

26 Szerkesztés menete: 1. A kezdőpontú félegyenesre c szksz felvétele A, B pontok; 2. A középpontú, b sugrú körív;. B középpontú, sugrú körív; 4. két körív metszéspontj C csúcs. (Jó úgy is, h szerkesztésben megszámozz lépéseket.) Szerkesztés: C b A c B 4 pont Kerület: K = + b + c K = 0 mm + 5 mm + 50 mm K = 115 mm = 11 és fél cm 4. ) 5; 8 b) 1; 2; 4; 5; 6; 8 c) 2; ; 4; 8 d) 1; 2; 5; 8 e) 2; 8 (Minden helyes szám 0,5 pont. H rossz is vn, kkor drbonként 0,5 pont levonás, de z összpontszám negtív nem lehet.) 5. ) c b b c; b c 26

27 b) c d b d c; d ; d b 6. 5 cm hosszúságú szksz körívek megrjzolás körzővel felezőmerőleges megrjzolás P Q 27

28 Tizedes törtek 1. megoldás Értelmezés, ábrázolás, egyszerűsítés, bővítés, kerekítés, műveletek, átlg 1,05 1 0,85 0,5 0,25 0 0,15 0,45 0,9 1 1,2 Számonként 0,5 pont 4 pont 1,2 > 1,05 > 0,9 > 0,45 > 0,15 > 0,25 > 0,5 > 0,85 2. ) Egészre: 25, Tizedre: 25,495 25,5 Százdr: 25,495 25,50 b) 0,9 = 0,90 > 0,12. 1 dkg = 0,1 kg 26 mm = 0,026 m 5,4 hl = 540 l = 540 dm 8,2 h = 8,2 60 min = 492 min cm 2 = 1,54 m 2 4. ) Becslés: = 108 Számolás: 168,2 59,76 = 108,44 Ellenőrzés: 108, ,76 = 168,2 b) Becslés: hánydos < 4 Számolás: 145,04 : 7 =,92 Ellenőrzés:,92 7 = 145,04 c) 2, + 97,7 : 10 = 2, + 9,77 = 12, = : 4 = 0,75 1 = 1 : 5 = 2,6 5 5 = 5 : 11 = 0, ,24 = = = ,918 = = Adtok: 4 db ötös; db négyes; 1 db hárms Terv: ( ) : 8 Számolás: ( ) : 8 = 5 : 8 = 4,75 jegyek átlg. 28

30 = 18 : 5 =,6 7 = 7 : 8 = 0,875 8 = : 11 = 0, ,6 = = = ,454 = = Adtok: ny: 5 év, p: 8 év, gyerekek: 2 év, 4 év és 7 év Terv: ( ) : 5 Számolás: ( ) : 5 = 86 : 5 = 17,2 év z átlgéletkoruk. 7. Adtok: ; 2,;.. Szbály: x 2 +,4. tg: 2, 2 +,4 = 4,6 +,4 = 8 1. tg: (2,,4) : 2 = 1,1 : 2 = 0,55 0

Pótvizsga anyaga 5. osztály (Iskola honlapján is megtalálható!) Pótvizsga: beadandó feladatok 45 perces írásbeli szóbeli a megadott témakörökből

Pótvizsga anyaga 5. osztály (Iskola honlapján is megtalálható!) Természetes számok: 0123 (TK 4-49.oldal) – tízes számrendszer helyi értékei alaki érték valódi érték – becslés kerekítés – alapműveletek:

MATEMATIKA FELADATLAP a 8. évfolyamosok számára

8. évfolym Mt2 feldtlp MATEMATIKA FELADATLAP 8. évfolymosok számár 15:00 ór NÉV: SZÜLETÉSI ÉV: HÓ: NAP: Tolll dolgozz! Zseszámológépet nem hsználhtsz. A feldtokt tetszés szerinti sorrenden oldhtod meg.

Matematika 5. osztály Osztályozó vizsga

Matematika 5. osztály Osztályozó vizsga A TERMÉSZETES SZÁMOK A tízes számrendszer A természetes számok írása, olvasása 1 000 000-ig. Helyi-értékes írásmód a tízes számrendszerben, a helyiérték-táblázat

TANMENET. Matematika

Bethlen Gábor Református Gimnázium és Szathmáry Kollégium 6800 Hódmezővásárhely, Szőnyi utca 2. Telefon: +36-62-241-703 www.bgrg.hu OM: 029736 TANMENET Matematika 2016/2017 5.A természettudományos képzés

Követelmény a 6. évfolyamon félévkor matematikából

Követelmény a 6. évfolyamon félévkor matematikából Gondolkodási és megismerési módszerek Halmazba rendezés adott tulajdonság alapján, részhalmaz felírása, felismerése. Két véges halmaz közös részének,

MATEMATIKA FELADATLAP a 8. évfolyamosok számára

8. évfolym AMt2 feltlp MATEMATIKA FELADATLAP 8. évfolymosok számár 15:00 ór NÉV: SZÜLETÉSI ÉV: HÓ: NAP: Tolll olgozz! Zseszámológépet nem hsználhtsz. A feltokt tetszés szerinti sorrenen olhto meg. Minen

Követelmény az 5. évfolyamon félévkor matematikából

Követelmény az 5. évfolyamon félévkor matematikából Gondolkodási és megismerési módszerek Néhány elem kiválasztása adott szempont szerint. Néhány elem sorba rendezése, az összes lehetséges sorrend felsorolása.

1. feladat Oldja meg a valós számok halmazán a következő egyenletet: 3. x log3 2

A 004/005 tnévi Országos Középiskoli Tnulmányi Verseny második fordulójánk feldtmegoldási MATEMATIKÁBÓL ( I ktegóri ) feldt Oldj meg vlós számok hlmzán következő egyenletet: log log log + log Megoldás:

2. tétel Egész számok – Műveletek egész számokkal. feleletvázlat

2. tétel Egész számok - Műveletek egész számokkal. feleletvázlat

1. tétel Természetes számok tízes számrendszer műveletek és tulajdonságaik Természetes számok, jele, jelölések, ábrázolása számegyenesen műveletek a természetes számok halmazán belül Tízes számrendszer

5. osztály. Matematika

5. osztály A természetes számok értelmezése 100 000-ig. A tízes számrendszer helyértékes írásmódja. A A természetes számok írásbeli összeadása, kivonása. A műveleti eredmények becslése. Ellenőrzés 3. A

TANMENETJAVASLAT. Dr. Korányi Erzsébet MATEMATIKA. tankönyv ötödikeseknek. címû tankönyvéhez

TANMENETJAVASLAT Dr. Korányi Erzsébet MATEMATIKA tankönyv ötödikeseknek címû tankönyvéhez A heti 3 óra, évi 111 óra B heti 4 óra, évi 148 óra Javaslat témazáró dolgozatra: Dr. Korányi Erzsébet: Matematika

MATEMATIKA FELADATLAP a 6. évfolyamosok számára

6. évfolym AMt1 feldtlp MATEMATIKA FELADATLAP 6. évfolymosok számár 2011. jnuár 21. 15:00 ór NÉV: SZÜLETÉSI ÉV: HÓ: NAP: Tolll dolgozz! Zseszámológépet nem hsználhtsz. A feldtokt tetszés szerinti sorrenden

Matematika 6. osztály Osztályozó vizsga

Matematika 6. osztály Osztályozó vizsga 1. Számok és műveletek 1. A tízes számrendszer Számok írása, olvasása, ábrázolása Az egymilliónál nagyobb természetes számok írása, olvasása. Számok tizedestört

Vizsgakövetelmények matematikából a 2. évfolyam végén

Vizsgakövetelmények matematikából az 1. évfolyam végén – – Ismert halmaz elemeinek adott szempont szerinti összehasonlítására, szétválogatására. Az elemek közös tulajdonságainak felismerésére, megnevezésére.

Minta feladatsor I. rész

Mint feldtsor I. rész. Írj fel z A számot htványként! A / pont/. Mekkor hosszúságú dróttl lehet egy m m-es tégllp lkú testet z átlój mentén felosztni két derékszögű háromszögre? Adj meg hosszúságot mértékegységgel!

MATEMATIKA FELADATLAP a 8. évfolyamosok számára

MATEMATIKA FELADATLAP 8. évfolymosok számár 11:00 ór NÉV: SZÜLETÉSI ÉV: HÓ: NAP: Tolll olgozz! Zseszámológépet nem hsználhtsz. A feltokt tetszés szerinti sorrenen olhto meg. Minen próálkozást, mellékszámítást

MATEMATIKA FELADATLAP a 8. évfolyamosok számára

8. évfolym Mt2 feldtlp MATEMATIKA FELADATLAP 8. évfolymosok számár 15:00 ór NÉV: SZÜLETÉSI ÉV: HÓ: NAP: Tolll dolgozz! Zsebszámológépet nem hsználhtsz. A feldtokt tetszés szerinti sorrendben oldhtod meg.

MATEMATIKA FELADATLAP a 8. évfolyamosok számára

8. évfolym Mt1 feldtlp MATEMATIKA FELADATLAP 8. évfolymosok számár 11:00 ór NÉV: SZÜLETÉSI ÉV: HÓ: NAP: Tolll dolgozz! Zseszámológépet nem hsználhtsz. A feldtokt tetszés szerinti sorrenden oldhtod meg.

Középiskolás leszek! matematika. 13. feladatsor 1. 2. 3. 4. 5. 6.

Középiskolás leszek! mtemtik Melyik számot jelentheti A h tudjuk hogy I felennyi mint S S egyenlõ K és O összegével K egyenlõ O és L különbségével O háromszoros L-nek L negyede 64-nek I + S + K + O + L

KOMPETENCIA ALAPÚ FELADATGYÛJTEMÉNY MATEMATIKÁBÓL 5. ÉVFOLYAM MEGOLDÁSOK

KOMPETENCIA ALAPÚ FELADATGYÛJTEMÉNY MATEMATIKÁBÓL 5. ÉVFOLYAM MEGOLDÁSOK 1. a) I; b) H; c) I; d) I; e) I.. a) I; b) I; c) H; d) I; e) H. Természetes számok. 5555 < 7788< 7878< 7887< 8787< 8877< 8888. 4.

Matematika. 1. évfolyam. I. félév

Matematika 1. évfolyam – Biztos számfogalom a 10-es számkörben – Egyjegyű szám fogalmának ismerete – Páros, páratlan fogalma – Sorszám helyes használata szóban – Növekvő, csökkenő számsorozatok felismerése

Tanmenetjavaslat. Téma Óraszám Tananyag Fogalmak Összefüggések Eszközök Kitekintés. Helyi érték, alaki érték. Számegyenes.

Heti 4 óra esetén, 37 tanítási hétre összesen 148 óra áll rendelkezésre. A tanmenet 132 óra beosztását tartalmazza. Heti 5 óra esetén összesen 37-tel több órában dolgozhatunk. Ez összesen 185 óra. Itt

MEGOLDÓKULCSOK. 1. feladatsor (1. osztály)

MEGOLDÓKULCSOK 1. feladatsor (1. osztály) 1. feladat 8 9 10 14 15 16 10 11 12 18 19 20 1. pontdoboz: Hibátlan számszomszédok írása 1 pont, hiba 0 pont. 2. feladat 20 17 14 11 8 5 2 2. pontdoboz: Szabályfelismerésért

Egyenes mert nincs se kezdő se végpontja

Szakasz mert van két végpontja Egyenes mert nincs se kezdő se végpontja Tört vonal Szög mert van két szára és csúcsa Félegyenes mert van egy kezdőpontja 5 1 1 Két egyenes egymásra merőleges ha egymással

Heves Megyei Középiskolák Palotás József és Kertész Andor Matematikai Emlékversenye évfolyam (a feladatok megoldása)

Okttási Hivtl E g r i P e d g ó g i i O k t t á s i K ö z p o n t Cím: 00 Eger, Szvorényi u. 7. Postcím: 00 Eger, Szvorényi u. 7. elefon: /50-90 Honlp: www.oktts.hu E-mil: POKEger@oh.gov.hu Heves Megyei

MATEMATIKA FELADATLAP a 8. évfolyamosok számára

8. évfolym TMt1 feldtlp MATEMATIKA FELADATLAP 8. évfolymosok számár tehetséggondozó változt 11:00 ór NÉV: SZÜLETÉSI ÉV: HÓ: NAP: Tolll dolgozz! Zseszámológépet nem hsználhtsz. A feldtokt tetszés szerinti

MATEMATIKA FELADATLAP a 8. évfolyamosok számára

2008. jnuár 26. MATEMATIKA FELADATLAP 8. évfolymosok számár 2008. jnuár 26. 11:00 ór M 1 feltlp NÉV: SZÜLETÉSI ÉV: HÓ: NAP: Tolll olgozz! Zseszámológépet nem hsználhtsz. A feltokt tetszés szerinti sorrenen

1. Végezd el a kijelölt mûveleteket a betûk helyére írt számokkal! Húzd alá azokat a mûveleteket,

Számok és mûveletek + b b + Összedásnál tgok felcserélhetõk. (kommuttív tuljdonság) ( + b) + c + (b + c) Összedásnál tgok csoportosíthtók. (sszocitív tuljdonság) b b ( b) c (b c) 1. Végezd el kijelölt

MATEMATIKA ÉRETTSÉGI 2007. október 25. KÖZÉPSZINT I.

MATEMATIKA ÉRETTSÉGI 007. október 5. KÖZÉPSZINT I. ) Az A hlmz elemei háromnál ngyobb egyjegyű számok, B hlmz elemei pedig húsznál kisebb pozitív pártln számok. Sorolj fel z hlmz elemeit! ( pont) A B AB

MATEMATIKA. 1. osztály

MATEMATIKA 1. osztály Gondolkodás tudjon egyszerű tárgyakat, elemeket sorba rendezni, összehasonlítani, szétválogatni legyen képes a halmazok számosságának megállapítására (20-as számkörben) használja

Az integrálszámítás néhány alkalmazása

Az integrálszámítás néhány lklmzás (szerkesztés ltt) Dr Toledo Rodolfo 4 november 4 Trtlomjegyzék Két függvények áltl htárolt terület Forgástestek térfogt és felszíne 5 3 Ívhosszszámítás 7 4 Feldtok 8

MATEMATIKA FELADATLAP a 8. évfolyamosok számára

8. évfolym Mt1 feldtlp MATEMATIKA FELADATLAP 8. évfolymosok számár 11:00 ór NÉV: SZÜLETÉSI ÉV: HÓ: NAP: Tolll dolgozz! Zsebszámológépet nem hsználhtsz. A feldtokt tetszés szerinti sorrendben oldhtod meg.

MATEMATIKA 9. osztály I. HALMAZOK. Számegyenesek, intervallumok

MATEMATIKA 9. osztály I. HALMAZOK Számegyenesek, intervllumok. Töltsd ki tábláztot! Minden sorbn egy-egy intervllum háromféle megdás szerepeljen!. Add meg fenti módon háromféleképpen következő intervllumokt!

1. Mit nevezünk egész számok-nak? Válaszd ki a következő számok közül az egész számokat: 3 ; 3,1 ; 1,2 ; -2 ; -0,7 ; 0 ; 1500

1. Mit nevezünk egész számok-nak? Válaszd ki a következő számok közül az egész számokat: 3 ; 3,1 ; 1,2 ; -2 ; -0,7 ; 0 ; 1500 2. Mit nevezünk ellentett számok-nak? Ábrázold számegyenesen a következő számokat

MATEMATIKA FELADATLAP a 8. évfolyamosok számára

Add meg az összeadásban szereplő számok elnevezéseit!

1. 2. 3. 4. Add meg az összeadásban szereplő számok elnevezéseit! Add meg a kivonásban szereplő számok elnevezéseit! Add meg a szorzásban szereplő számok elnevezéseit! Add meg az osztásban szereplő számok

1. Mit nevezünk egész számok-nak? Válaszd ki a következő számok közül az egész számokat: 3 ; 3,1 ; 1,2 ; -2 ; -0,7 ; 0 ; 1500

Pótvizsga matematika 7. osztály (Iskola honlapján is megtalálható!) Tételek

Pótvizsga matematika 7. osztály (Iskola honlapján is megtalálható!) Tételek 1. Hatványozás 2. Normálalak. Mértékegységek. Műveletek racionális számokkal (tört, tizedes tört) 5. Középpontos tükrözés 6.

MATEMATIKA TANMENET SZAKKÖZÉPISKOLA. 9. Nyelvi előkészítő osztály

MINŐSÉGIRÁNYÍTÁSI ELJÁRÁS MELLÉKLET Tanmenetborító Azonosító: ME-III.1./1 Változatszám: 2 Érvényesség 2013. 01. 01. kezdete: Oldal/összes: 1/6 Fájlnév: ME- III.1.1.Tanmenetborító SZK- DC-2013 MATEMATIKA

Exponenciális és logaritmikus egyenletek, egyenletrendszerek, egyenlôtlenségek

Eponenciális és logritmikus egyenletek, Eponenciális és logritmikus egyenletek, egyenletrendszerek, egyenlôtlenségek Eponenciális egyenletek 60 ) = ; b) = ; c) = ; d) = 0; e) = ; f) = ; g) = ; h) =- 7

Matematika. 1. osztály. 2. osztály

Matematika 1. osztály – képes halmazokat összehasonlítani az elemek száma szerint, halmazt alkotni; – képes állítások igazságtartalmának eldöntésére, állításokat megfogalmazni; – halmazok elemeit összehasonlítja,

Matematika (alsó tagozat)

Matematika (alsó tagozat) Az értékelés elvei és eszközei A tanév során az értékelés alapja a tanulók állandó megfigyelése. Folyamatos fejlesztő célzatú szóbeli értékelés visszajelzést ad a tanuló számára

Differenciálszámítás. Lokális szélsőérték: Az f(x) függvénynek az x 0 helyen lokális szélsőértéke

Differenciálszámítás Lokális növekedés (illetve csökkenés): H z f() függvény deriváltj z 0 helyen pozitív: f () > 0 (illetve negtív: f () < 0), kkor z f() függvény z 0 helyen növekvően (illetve csökkenően)

JAVÍTÓKULCSOK Számfogalom

JAVÍTÓKULCSOK Számfogalom Számok írása 1. a) 17 f) 260 b) 39 g) 422 c) 99 h) 668 d) 101 i) 707 e) 206 j) 999 2. a) tizennégy f) háromszázötven b) negyvennyolc g) ötszázkilencvenegy c) nyolcvanhét h) hétszázhúsz

Matematikai feladatlap T9-2013

Keresztnév: Vezetéknév: TESZTFORM Mtemtiki feldtlp Test z mtemtiky eloslovenské testovnie žikov 9. roèník ZŠ ZONOSÍTÓ SZÁM T9-57 Kedves tnulók, mtemtiki feldtlpot kptátok kézhez. teszt feldtot trtlmz.

A fejlesztés várt eredményei a 1. évfolyam végén

A tanuló legyen képes: A fejlesztés várt eredményei a 1. évfolyam végén – Halmazalkotásra, összehasonlításra az elemek száma szerint; – Állítások igazságtartalmának eldöntésére, állítások megfogalmazására;

Borbély Sándor Országos Tanulmányi Verseny. Vác Matematika. 5. osztály. Megoldókulcs. Név: Iskola:

Borbély Sándor Országos Tanulmányi Verseny Vác 201 Matematika 5. osztály Megoldókulcs Név: Iskola: 1. Pótold a hiányzó számokat! A Fővárosi Állat- és Növénykert története: 1. -ban nyílt meg. 1866 2. -ban

Racionális számok: Azok a számok, amelyek felírhatók két egész szám hányadosaként ( p q

Szóbeli tételek matematikából 1. tétel 1/a Számhalmazok definíciója, jele (természetes számok, egész számok, racionális számok, valós számok) Természetes számok: A pozitív egész számok és a 0. Jele: N

Vezetéknév. Utónév. Osztály. Iskola. Mate gyűjtemény EDITURA PARALELA 45

Vezetéknév. Utónév. Osztály. Iskola. Mate 2000+ gyűjtemény Jelen kiadvány az érvényben lévő Tanterv alapján készült, melyet a Nemzeti Oktatási Minisztérium 5003/2.12.2014-es határozatszámmal

6. OSZTÁLY. Az évi munka szervezése, az érdeklõdés felkeltése Feladatok a 6. osztály anyagából. Halmazok Ismétlés (halmaz megadása, részhalmaz)

6. OSZTÁLY Óraszám 1. 1. Az évi munka szervezése, az érdeklõdés felkeltése a 6. osztály anyagából Tk. 13/elsõ mintapélda 42/69 70. 96/elsõ mintapélda 202/16. 218/69. 2 3. 2 3. Halmazok Ismétlés (halmaz

Fényi Gyula Jezsuita Gimnázium és Kollégium Miskolc, Fényi Gyula tér Tel.: (+36-46) , , , Fax: (+36-46)

Fényi Gyula Jezsuita Gimnázium és Kollégium 529 Miskolc, Fényi Gyula tér 2-12. Tel.: (+6-46) 560-458, 560-459, 560-58, Fax: (+6-46) 560-582 E-mail: fenyi@jezsuita.hu Honlap: www.jezsu.hu A JECSE Jesuit

MATEMATIKA FELADATLAP a 6. évfolyamosok számára

2007. jnuár 26. MATEMATIKA FELADATLAP 6. évfolymosok számár 2007. jnuár 26. 15:00 ór M 1 feltlp NÉV: SZÜLETÉSI ÉV: HÓ: NAP: A feltokt tetszés szerinti sorrenen olhto meg. Minen próálkozást, mellékszámítást

1. osztály. Gondolkodási módszerek alapozása A tanuló:

Gondolkodási módszerek alapozása 1. osztály tudjon számokat, elemeket sorba rendezni, összehasonlítani, szétválogatni legyen képes a halmazok számosságának megállapítására, használja helyesen a több, kevesebb,

a b a leghosszabb. A lapátlók által meghatározott háromszögben ezzel szemben lesz a

44 HANCSÓK KÁLMÁN MEGYEI MATEMATIKAVERSENY MEZŐKÖVESD, évfolym MEGOLDÁSOK Mutssuk meg, hogy egy tetszőleges tégltest háromféle lpátlójából szerkesztett háromszög hegyesszögű lesz! 6 pont A tégltest egy

Egy látószög – feladat

Egy látószög - feladat

Ehhez tekintsük z 1. ábrát is! Egy látószög – feldt 1. ábr Az A pont körül kering C pont, egy r sugrú körön. A rögzített A és B pontok egymástól távolság vnnk. Az = CAB szöget folymtosn mérjük. Keressük

2018/2019. Matematika 10.K

Egész éves dolgozat szükséges felszerelés: toll, ceruza, radír, vonalzó, körző, számológép, függvénytáblázat 2 órás, 4 jegyet ér 2019. május 27-31. héten Aki hiányzik, a következő héten írja meg, e nélkül

MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Koordináta-geometria

MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Koordináta-geometria A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett

MATEMATIKA FELADATLAP a 8. évfolyamosok számára

MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT. Koordináta-geometria

MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT 1) Adott két pont: A 4; 1 felezőpontjának koordinátáit! AB felezőpontja legyen F. Koordináta-geometria és B 3 1; Írja fel az AB szakasz 1 3 4

Osztályozóvizsga követelményei

Osztályozóvizsga követelményei Képzés típusa: Tantárgy: Általános iskola Matematika Évfolyam: 1 Emelt óraszámú csoport Emelt szintű csoport Vizsga típusa: Írásbeli Követelmények, témakörök: Halmazok összehasonlítása

Scherlein Márta Dr. Hajdu Sándor Köves Gabriella Novák Lászlóné MATEMATIKA 4. A FELMÉRŐ FELADATSOROK ÉRTÉKELÉSE

Scherlein Márta Dr. Hajdu Sándor Köves Gabriella Novák Lászlóné MATEMATIKA 4. A FELMÉRŐ FELADATSOROK ÉRTÉKELÉSE A tájékozódó felmérő feladatsorok értékelése A tájékozódó felmérések segítségével a tanulók

Trigonometria. Szögfüggvények alkalmazása derékszög háromszögekben. Szent István Egyetem Gépészmérnöki Kar Matematika Tanszék 1

Szent István Egyetem Gépészmérnöki Kar Matematika Tanszék 1 Trigonometria Szögfüggvények alkalmazása derékszög háromszögekben 1. Az ABC hegyesszög háromszögben BC = 14 cm, AC = 1 cm, a BCA szög nagysága

MATEMATIKA FELADATLAP a 6. évfolyamosok számára

6. évfolym Mt1 feltlp MATEMATIKA FELADATLAP 6. évfolymosok számár 2015. jnuár 17. 11:00 ór NÉV: SZÜLETÉSI ÉV: HÓ: NAP: Tolll olgozz! Zseszámológépet nem hsználhtsz. A feltokt tetszés szerinti sorrenen

MATEMATIKA FELADATLAP a 6. évfolyamosok számára

6. évfolym Mt1 feltlp MATEMATIKA FELADATLAP 6. évfolymosok számár 2013. jnuár 18. 15:00 ór NÉV: SZÜLETÉSI ÉV: HÓ: NAP: Tolll olgozz! Zseszámológépet nem hsználhtsz. A feltokt tetszés szerinti sorrenen

MATEMATIKA FELADATLAP a 6. évfolyamosok számára

6. évfolym AMt2 feldtlp MATEMATIKA FELADATLAP 6. évfolymosok számár 2011. jnuár 27. 15:00 ór NÉV: SZÜLETÉSI ÉV: HÓ: NAP: Tolll dolgozz! Zseszámológépet nem hsználhtsz. A feldtokt tetszés szerinti sorrenden

MEGOLDÁSOK 1 TERMÉSZETES SZÁMOK 1.1 A TERMÉSZETES SZÁMOK 5. OLDAL 1.2 A TERMÉSZETES SZÁMOK RENDEZÉSE 7. OLDAL. 6. A szám helyi érték szerinti bontása

M TERMÉSZETES SZÁMOK. TERMÉSZETES SZÁMOK. OLDL.. Kisebbik egyes számszomszéd 0 0 0 0 0 0 0 0 szám 00 0 00 0 0 0 0 0 0 00 000 Nagyobbik egyes számszomszéd 0 000 0 0 0 00 0 000 0 0 0 00 00 00 Legnagyobb

JAVÍTÓKULCSOK I. Számfogalom

JAVÍTÓKULCSOK I. Számfogalom Számok írása 1. a) 17 f) 260 b) 39 g) 422 c) 99 h) 668 d) 101 i) 707 e) 206 j) 999 2. a) tizennégy f) háromszázötven b) negyvennyolc g) ötszázkilencvenegy c) nyolcvanhét h)

Háromszögek, négyszögek, sokszögek 9. évfolyam

Háromszögek, négyszögek, sokszögek 9. évfolyam I. Pontok, egyenesek, síkok és ezek kölcsönös helyzetet 1) a pont, az egyenes, a sík és az illeszkedés alapfogalmak 2) két egyenes metsző, ha van közös pontjuk

NÉGYOSZTÁLYOS FELVÉTELI Részletes megoldás és pontozás a Gyakorló feladatsor I-hez

NÉGYOSZTÁLYOS FELVÉTELI Részletes megoldás és pontozás a Gyakorló feladatsor I-hez Számadó László (Budapest) 1. Számold ki! a) 1 2 3 + 4 5 6 ; b) 1 2 3 + 4 5 6. 2 3 4 5 6 7 2 3 5 6 7 a) 1 2 3 4 2 3 4 +5

A 2013/2014. tanévi Országos Középiskolai Tanulmányi Verseny első forduló MATEMATIKA I. KATEGÓRIA (SZAKKÖZÉPISKOLA) Javítási-értékelési útmutató

Okttási Hivtl A 013/014 tnévi Országos Középiskoli Tnulmányi Verseny első forduló MATEMATIKA I KATEGÓRIA (SZAKKÖZÉPISKOLA) Jvítási-értékelési útmuttó 1 Oldj meg vlós számok hlmzán egyenletet! 3 5 16 0

MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Koordináta-geometria

MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Koordináta-geometria A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett

MATEMATIKAI KOMPETENCIATERÜLET A

MATEMATIKAI KOMPETENCIATERÜLET A Matematika 5. évfolyam eszközök tanárok részére 1. félév A kiadvány az Educatio Kht. Kompetenciafejlesztő oktatási program kerettanterve alapján készült. A kiadvány a Nemzeti

Dudás Gabriella Hetényiné Kulcsár Mária Machánné Tatár Rita Sós Mária. sokszínû. 5 gyakorló. kompetenciafejlesztõ munkafüzet. 2.

Dudás Gabriella Hetényiné Kulcsár Mária Machánné Tatár Rita Sós Mária sokszínû gyakorló kompetenciafejlesztõ munkafüzet. kötet Mozaik Kiadó Szeged, Színesrúd-készlet. Törtek bõvítése és egyszerûsítése

MATEMATIKA FELADATLAP a 8. évfolyamosok számára

Matematika érettségi 2015 május 5

( ) A 6-tl vló oszthtóság feltétele, hogy szám oszthtó legyen -vel és -ml. 60 6 64 66 68 X X A minden tgdás: vn olyn A brn tgdás: nem brn Vn olyn szekrény, melyik nem brn (A) A D 49 b 4 ( 0)

EÖTVÖS LORÁND SZAKKÖZÉP- ÉS SZAKISKOLA TANÍTÁST SEGÍTŐ OKTATÁSI ANYAGOK MÉRÉS TANTÁRGY

EÖTVÖS LORÁND SZAKKÖZÉP- ÉS SZAKISKOLA TANÍTÁST SEGÍTŐ OKTATÁSI ANYAGOK MÉRÉS TANTÁRGY ALAPMÉRTÉKEGYSÉGEK A fizikában és a méréstudományban mértékegységeknek hívjuk azokat a méréshez használt egységeket,

4. évfolyam A feladatsor

Név: 4. évfolyam A feladatsor Osztály: Kedves Vizsgázó! Olvasd el figyelmesen a feladatokat, gondold át a megoldások menetét! Eredményes, sikeres munkát kívánunk!. a) Írd le számjegyekkel! Rendezd a számokat

MATEMATIKA FELADATLAP a 8. évfolyamosok számára

7. tétel: Elsı- és másodfokú egyenletek és egyenletrendszerek megoldási módszerei

7. tétel: Elsı- és másodfokú egyenletek és egyenletrendszerek megoldási módszerei Elsıfokú függvények: f : A R A R, A és f () = m, hol m; R m 0 Az elsıfokú függvény képe egyenes. (lásd késı) m: meredekség,

JAVÍTÓKULCSOK I. Természetes számok

JAVÍTÓKULCSOK I. Természetes számok Bevezetı feladatok 1. a) b) c) d) e) 2. a) A = 5; B = 45; C = 55; D = 30; E = 20 b) A = 120; B = 160; C = 220; D = 235; E = 285 c) A = 1000; B = 1300; C = 1900; D =

A kompetencia alapú matematika oktatás. tanmenete a 9. osztályban. Készítette Maitz Csaba

A kompetencia alapú matematika oktatás tanmenete a 9. osztályban Készítette Maitz Csaba Szerkesztési feladatok 1. Síkgeometriai alapfogalmak 2. Egyszerűbb rajzok, szerkesztések körző, vonalzó használata

Geometriai feladatok, 9. évfolyam

Geometriai feladatok, 9. évfolyam Szögek 1. Nevezzük meg az ábrán látható szögpárokat. Mekkora a nagyságuk, ha α =52 o fok? 2. Mekkora az a szög, amelyik a, az egyenesszög 1/3-ad része b, pótszögénél 32

Skaláris szorzat: a b cos, ahol α a két vektor által bezárt szög.

1 Összeadás: Legyen a (7; 3) és b (- 2; 4), akkor az összegük a + b (7 + (-2); 3 + 4) = (5; 7) Kivonás: Legyen a (7; 3) és b (- 2; 4), akkor a különbségük a b (7 – (-2); 3-4)=(9; – 1) Valós számmal való

Koordinátageometria Megoldások

005-0XX Középszint Koordinátageometria Megoldások 1) Adott két pont: A 4; 1 felezőpontjának koordinátáit! AB felezőpontja legyen F. és B 3 1; Írja fel az AB szakasz 1 3 + 4 + 1 3 F ; = F ;1 ) Egy kör sugarának

Matematika felső tagozat

Matematika felső tagozat 5. évfolyam Témakör 1. Gondolkodási módszerek 2. Számtan, algebra 3. Összefüggések, függvények, sorozatok 4. Geometria, mérés I. félév Követelmény A gondolkodási módszerek követelményei

Differenciálgeometria feladatok

Differenciálgeometri feldtok 1. sorozt 1. Egy sugrú kör csúszás nélkül gördül egy egyenes mentén. A kör egy rögzített kerületi pontj áltl leírt pályát cikloisnk nevezzük. () Írjuk fel ciklois egy c: R

Matematika A1a – Analízis elméleti kérdései

Matematika A1a - Analízis elméleti kérdései

Mtemtik A1 – Anlízis elméleti kérdései (műszki menedzser szk, 2018. ősz) Kör egyenlete Az (x 0, y 0 ) középpontú, R sugrú kör egyenlete síkon (x x 0 ) 2 + (y y 0 ) 2 = R 2. Polinom Az x n x n + n 1 x n

Osztályozóvizsga-tematika 8. évfolyam Matematika

Osztályozóvizsga-tematika 8. évfolyam Matematika 1. félév 1. Gondolkozz és számolj! A természetes szám fogalma, műveleti tulajdonságok Helyiértékek rendszere a tízes számrendszerben: alakiérték, tényleges

MATEMATIKA FELADATLAP

MATEMATIKA FELADATLAP 8. évfolymosok számár tehetséggonozó változt :00 ór NÉV: SZÜLETÉSI ÉV: HÓ: NAP: Tolll olgozz! Zseszámológépet nem hsználhtsz. A feltokt tetszés szerinti sorrenen olhto meg. Minen

Bevezetés. Alapműveletek szakaszokkal geometriai úton

011.05.19. Másodfokú egyenletek megoldás geometrii úton evezetés A középiskoli mtemtik legszerteágzóbb része másodfokú egyenletek megoldás. A legismertebb módj természetesen megoldóképlet hsznált. A képlet

Tehetetlenségi nyomatékok

Tehetetlenségi nyomtékok 1 Htározzuk meg z m tömegű l hosszúságú homogén rúd tehetetlenségi nyomtékát rúd trtóegyenesét metsző tetszőleges egyenesre vontkozón, h rúd és z egyenes hjlásszöge α, rúd középpontjánk

MATEMATIKA FELADATLAP a 8. évfolyamosok számára

FELVÉTELI VIZSGA, július 15.

BABEŞ-BOLYAI TUDOMÁNYEGYETEM, KOLOZSVÁR MATEMATIKA ÉS INFORMATIKA KAR FELVÉTELI VIZSGA, 8. július. Írásbeli vizsg MATEMATIKÁBÓL FONTOS TUDNIVALÓK: ) A feleletválsztós feldtok (,,A rész) esetén egy vgy

Munkafüzet megoldások 7. osztályos tanulók számára. Makara Ágnes Bankáné Mező Katalin Argayné Magyar Bernadette Vépy-Benyhe Judit

Kalandtúra 7. unkafüzet megoldások 7. osztályos tanulók számára akara Ágnes Bankáné ező Katalin Argayné agyar Bernadette Vépy-Benyhe Judit BEELEGÍTŐ GONDOLKODÁS. SZÓRAKOZTATÓ FELADVÁNYOK. oldal. 6. 6.

Nagy Erika. Matekból Ötös. 5. osztályosoknak. www.matek.info

Nagy Erika Matekból Ötös 5. osztályosoknak www.matek.info 1 Készítette: Nagy Erika 2009 Javított kiadás 2010 MINDEN JOG FENNTARTVA! Jelen kiadványt vagy annak részeit tilos bármilyen eljárással (elektronikusan,

MATEMATIKA FELADATLAP a 8. évfolyamosok számára

MATEMATIKA a 8. évfolyamosok számára. Mat2 JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ

8. évfolyam Mat Javítási-értékelési útmutató MATEMATIKA a 8. évfolyamosok számára Mat JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ A javítási-értékelési útmutatóban feltüntetett válaszokra a megadott pontszámok adhatók.

MILYEN ÚJDONSÁGOK VANNAK AZ OFI ÚJ TANKÖNYVEIBEN? OSZTÁLY

A NEMZETI ALAPTANTERVHEZ ILLESZKEDŐ TANKÖNYV, TANESZKÖZ ÉS NEMZETI KÖZOKTATÁSI PORTÁL FEJLESZTÉSE TÁMOP-3.1.2-B/13-2013-0001 MILYEN ÚJDONSÁGOK VANNAK AZ OFI ÚJ TANKÖNYVEIBEN? 5-6-7. OSZTÁLY KEDVES ÖTÖDIKES!

Hatvani István fizikaverseny 2015-16. 1. forduló megoldások. 1. kategória

1. ktegóri 1.1.1. Adtok: ) Cseh László átlgsebessége b) Chd le Clos átlgsebessége Ezzel z átlgsebességgel Cseh László ideje ( ) ltt megtett távolság Így -re volt céltól. Jn Switkowski átlgsebessége Ezzel

Hatványozás és négyzetgyök. Másodfokú egyenletek

Defiíció: R, Z Htváyozás és égyzetgyök 0 h 0. ( téyezős szorzt) h h 0, 0. A htváyozás zoossági: : m ( ) m m m m m Defiíció: Az x vlós szám ormállkják evezzük z hol 0 és egész szám. 0 kifejezést, h x