Gyermeked nehezen boldogul a 11. osztályos matekkal

1. Biztos, hogy más! Egyrészt nem száraz tankönyv, ami a mai fiataloknál hatalmas előnyt jelent. Interaktivitást igényel! Gyermekednek kell beírnia, összekötni, kijelölnie, sorrendbe helyeznie a megoldásokat.

Geőcze Zoárd matematikaverseny

A verseny célja Lehetőséget biztosítani a Kárpátalja magyar iskoláiban tanuló általános és középiskolás diákok számára, hogy összemérhessék matematikai tudásukat, logikus gondolkodási képességüket.

A verseny célja

Lehetőséget biztosítani a Kárpátalja magyar iskoláiban tanuló általános és középiskolás diákok számára, hogy összemérhessék matematikai tudásukat, logikus gondolkodási képességüket évfolyamtársaikkal.

A verseny névadója, a magyar matematika tudomány egyik büszkesége. 1899-től az ungvári alreál iskolában tanított.

A verseny lebonyolítása

A Geőcze Zoárd matematika emlékverseny klasszikus feladatmegoldó verseny. Évfolyamonként 5 feladatot kell (4 algebra, 1 mértan) megoldani. A feladatok megoldására 3 óra áll rendelkezésre. Minden feladatot 1-10 pont között értékelnek.

A versenyen az általános és középiskolák 7–11. évfolyamára járó diákjai vehetnek részt iskolatípustól függetlenül.

A feladatok összeállításánál az Ukrajnában elfogadott állami tanterv alapján a megnevezett szerzők által írt tankönyveket, illetve a tanmenetnek megfelelő fejezeteket és témákat vesszük figyelembe.

A vetélkedőn egy feladat a GENIUS tehetségpontok tematikájához kapcsolódik.

7. osztály: Algebra, Mértan / H. P. Bevz, V. H. Bevz, N. H. Vladimirova

8. osztály: Algebra, Mértan /A. H. Merzljak, V. B. Polonszkij, M. Sz. Jakir, M.I. Burda, N. A. Taraszenkova

9. osztály: Algebra, Mértan / H. P. Bevz, M. I. Burda, N. A. Taraszenkova

10. osztály: Algebra, Mértan / J. P. Nelin, M. I. Burda, N. A. Taraszenkova

11. osztály: Matematika / H. P. Bevz, V. H. Bevz

A feladatok megoldása során az elérhető maximális pontérték 100

Jelentkezési határidő: 2014. február 22.

A verseny helyszíne: II. Rákóczi Ferenc Kárpátaljai Magyar Főiskola, 90202 Beregszász, Kossuth Lajos tér 6.

Matematika 11 osztály feladatok megoldással

Vissza

vagy regisztrálj a következő fiókjaid egyikével

Letelt az ehhez a blokkhoz tartozó időkeret!

A blokk végéhez értél.

A dolgozat kitöltésének határideje lejárt!

A dolgozat kitöltésére szánt időkeret lejárt!

Válaszd ki a csoportodat, akiknek feladatot szeretnél kiosztani!

Hozd létre a csoportodat a Személyes címtáradban, akiknek feladatot szeretnél kiosztani!

Egyenletek – feladatok és megoldások

egyenlet feladatok és megoldások

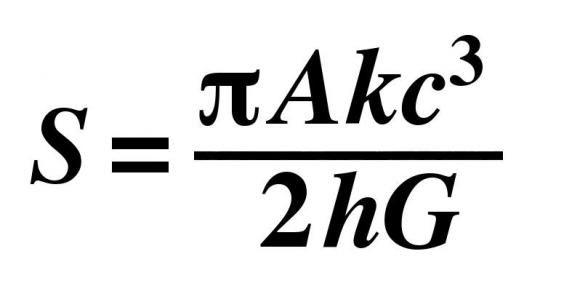
y 2 – 5y – 24 = y 2 – 5y + 2 (y + 6)
y 2 – 5y – 24 = y 2 – 5y + 2y + 12
y 2 – 5y – 24 = y 2 – 3y + 12
y 2 – 5y – 24 + 24 = y 2 – 3y + 12 + 24
y 2 – 5y = y 2 – 3y + 36
y 2 – 5y – (y 2 – 3y) = y 2 – 3y + 36 – (y 2 – 3y)
-2y = 36
y = -18

MEGOLDÁS

y 2 – 6y – 16 = y 2 – 4y – 8
y 2 – 6y – 16 + 16 = y 2 – 4y – 8 + 16
y 2 – 6y = y 2 – 4y + 8
y 2 – 6y – (y 2 – 4y) = y 2 – 4y + 8 – (y 2 – 4y)
-2y = 8
y = -4

MEGOLDÁS

2z 2 – z – 15 = 2z 2 – 14z + 11
2z 2 – z – 15 + 15 = 2z 2 – 14z + 11 + 15
2z 2 – z = 2z 2 – 14z + 26
2z 2 – z – (2z 2 – 14z) = 2z 2 – 14z + 26 – (2z 2 – 14z)
13z = 26

z = 2

MEGOLDÁS

-6 ≠ -14 ellentmondás nincs megoldás

MEGOLDÁS

x 2 – 2x + 1 = x 2 – x – 6
x 2 – 2x + 1 – 1 = x 2 – x – 6 – 1
x 2 – 2x = x 2 – x – 7
x 2 – 2x – (x 2 – x) = x 2 – x – 7 – (x 2 – x)
-x = -7
x = 7

MEGOLDÁS

x 2 + 10x + 25 = x 2 + 2x + 9
x 2 + 10x + 25 – 25 = x 2 + 2x + 9 – 25
x 2 + 10x = x 2 + 2x – 16
x 2 + 10x – (x 2 + 2x) = x 2 + 2x – 16 – (x 2 + 2x)

8x = -16
x = -2

MEGOLDÁS

x 2 – 4 = x 2 + 2x . 6 + 6 2
x 2 – 4 = x 2 + 12x + 36
x 2 – 4 + 4 = x 2 + 12x + 36 + 4
x 2 = x 2 + 12x + 40
x 2 – (x 2 + 12x) = x 2 + 12x + 40 – (x 2 + 12x)
-12x = 40

MEGOLDÁS

(3z) 2 – 2 . 3z . 1 + 1 2 = 3z . 3z + 3z (-5 ) + 4 . 3z + 4 (-5)
9z 2 – 6z + 1 = 9z 2 – 3z – 20
9z 2 – 6z + 1 – 1 = 9z 2 – 3z – 20 -1
9z 2 – 6z = 9z 2 – 3z – 21
9z 2 – 6z – (9z 2 – 3z) = 9z 2 – 3z – 21 – (9z 2 – 3z)
-3z = -21
z = 7

Fejezd ki a kérdezett ismeretlent a megadott képletekből!

MEGOLDÁS

Szöveges feladatok

Ha egy szám harmadából kivonjuk a negyedét, akkor eredményül 7-et kapunk. Melyik ez a szám?

MEGOLDÁS

ELLENŐRZÉS

$\begin{pmatrix} \frac{84}{3} = 28 \end{pmatrix} - \begin{pmatrix} \frac{84}{4} = 21 \end{pmatrix} \Rightarrow 28 - 21 = 7$

MEGOLDÁS

$x + \frac{x}{3} + \frac{x}{4} = 190 \Rightarrow x = 120$

ELLENŐRZÉS

$120 +\begin{pmatrix} \frac{120}{3} = 40 \end{pmatrix} + \begin{pmatrix} \frac{120}{4} = 30 \end{pmatrix} \Rightarrow 120 + 40 + 30 = 190$

MEGOLDÁS

$\frac{x}{2} + \frac{x}{3} + \frac{x}{4} = x +3 \Rightarrow x = 36$

ELLENŐRZÉS

$\begin{pmatrix} \frac{36}{2} = 18 \end{pmatrix} + \begin{pmatrix} \frac{36}{3} = 12 \end{pmatrix} + \begin{pmatrix} \frac{36}{4} = 9 \end{pmatrix}\Rightarrow (18 + 12 + 9 = 39) = (36 + 3 =39)$

Feladatok másodfokú egyenletekre

Oldd meg a következő egyenleteket a valós számok halmazán!

MEGOLDÁS

$\frac{3 \pm \sqrt{(-3)^2 - 4 * 1 * (-10)}} {2 * 1}$

MEGOLDÁS

$\frac{14 \pm \sqrt{(-14)^2 - 4 * 1 * 49}} {2 * 1}$

MEGOLDÁS

⇒ gyök alatt negatív szám nincs megoldás

MEGOLDÁS

$\frac{22 \pm \sqrt{(-22)^2 - 4 * 1 * 121}} {2 * 1}$

MEGOLDÁS

⇒ gyök alatt negatív szám nincs megoldás

MEGOLDÁS

$\frac{7 \pm \sqrt{(-7)^2 - 4 * 1 * (-10)}} {2 * 1}$

MEGOLDÁS

$\frac{1 \pm \sqrt{(-1)^2 - 4 * 1 * (-20)}} {2 * 1}$

MEGOLDÁS

Add meg a következő gyökök másodfokú egyenletét, gyöktényezős alakban!

MEGOLDÁS

$(x - \frac{2} {3}) * (x - 3) = x^2 - \frac{11} {3}x + 2$

MEGOLDÁS

$(x - \frac{1} {4}) * (x - 4) = x^2 - \frac{5} {4}x + 1$

MEGOLDÁS

$(x - \frac{3} {4}) * (x - \frac{4} {3}) = x^2 - \frac{25} {12}x + 1$

MEGOLDÁS

$(x + \frac{5} {6}) * (x - \frac{2} {5}) = x^2 - \frac{13} {30}x - \frac{1} {3}$

Írd fel a következő polinomokat egész számokkal szorzatalakba!

MEGOLDÁS

Szöveges feladatok

Egy n oldalú sok szögnek

átlója van. Hány oldalú a sokszög, ha összesen 54 átlója van?

MEGOLDÁS

⇒ n * (n – 3) = 108 ⇒ n 2 – 3n – 108 = 0 ⇒ x = 12

MEGOLDÁS

a . b = 320 cm 2 és a – 4 = b ⇒ a = b + 4
(b + 4) . b = 320 ⇒ b 2 + 4b – 320 = 0
⇒ b = 16 cm ⇒ a = 20 cm

MEGOLDÁS

a . b = 140 cm 2 és a + 1 = 3b ⇒ a = 3b – 1
(3b – 1) . b = 140 ⇒ 3b 2 – b – 140 = 0
⇒ b = 7 cm ⇒ a = 20 cm

MEGOLDÁS

2 . (a + b) = 70 cm a . b = 300 cm 2 ⇒ 35 – b = a
(35 – b) . b = 300 ⇒ b 2 – 35b + 300 = 0
⇒ b₁ = 15 cm ⇒ a₁ = 20 cm
⇒ b₂ = 20 cm ⇒ a₂ = 15 cm

Feladatok magasabb fokú egyenletekre

Oldd meg a következő egyenleteket a valós számok halmazán!

MEGOLDÁS

t = x 2 = 4 ⇒ x₁ = -2 x₂ = 2 és x 2 = 1 ⇒ x₃ = -1 x₄ = 1

MEGOLDÁS

t = x 2 = 16 ⇒ x₁ = -4 x₂ = 4 és x 2 = 4 ⇒ x₃ = -2 x₄ = 2

MEGOLDÁS

t = x 2 = 5 ⇒ x₁ = -\sqrt x₂ = \sqrt és x 2 = 2 ⇒ x₃ = -\sqrt x₄ = \sqrt

MEGOLDÁS

t = x 2 = 3 ⇒ x₁ = -\sqrt x₂ = \sqrt és x 2 = -1 nincs megoldás

Feladatok elsőfokú egyenletrendszerekre

I. 4x + 3y = 14
II. 2x – y = 12

MEGOLDÁS

I. -4x – y = 40
II. x + 5y = 9

MEGOLDÁS

I. 2x – 6y = 6
II. 5x + 3y = 42

MEGOLDÁS

I. 4x + 2y =4
II. -6x + 3y = 33

MEGOLDÁS

I. 12x + 11y = 18
II. 16x – 7y = -12

MEGOLDÁS

I. 12x + 11y = 18 /*4 ⇒ I. 48x + 44y = 72 II. 16x – 7y = -12 /* (-3) ⇒ II. -48x + 21y = 36 ⇒ I. + II. 65y = 108 ⇒ y = \frac és 16x – 7 *\frac = -12 ⇒ x = -\frac

I. 3x – 10y = 3
II. -9x + 24y = -10

MEGOLDÁS

-6y = -1 ⇒ y = \frac és 3x – 10 * \frac = 3 ⇒ x = \frac = \frac

I. 14x – 8y = 10
II. -21x + 15y = 60

MEGOLDÁS

6y = 150 ⇒ y = 25 és x = 15

I. 18x + 24y = -132
II. 27x – 40y = 676

MEGOLDÁS

I. + II. ⇒ 152y = -1748 ⇒ y = -11,5 és x = 8

I. 2x + 3y + 5 = 5x + 6y – 1
II. x – 4y 2 = 2x – 2y

MEGOLDÁS

I. 3 . (x + 5) = 2 . (2y – 1)
II. 4 . (3x – 6) = 3 . (y + 4)

MEGOLDÁS

I. 3 * (x + 5) = 2 * (2y – 1) ⇒ I. 3x – 4y = -17 /* 4 ⇒ I. -12x + 16y = 68 II. 4 * (3x – 6) = 3 * (y + 4) ⇒ II. 12x – 3y = 36

I. + II. ⇒ 13y = 104 ⇒ y = 8 és x = 5

I. 5 . (2x + y) = 4 . (3y – 5x) + 13
II. 6 . (8x – 2y + 6) = 4 . (2y – 3x) – 4

MEGOLDÁS

I. 5 * (2x + y) = 4 * (3y – 5x) + 13 ⇒ I. 30x – 7y = 13 /* (-2) ⇒ I. -60x + 14y = -26 II. 6 * (8x – 2y + 6) = 4 * (2y – 3x) – 4 ⇒ II. 60x – 20y = -40

I. + II. ⇒ -6y = -66 ⇒ y = 11 és x = 3

I. 2 . (2x + 3y ) = 3 . (3x – y) + 5
II. 4 . (3x – 4y) = 2 . (x + y) – 10

MEGOLDÁS

I. 2 * (2x + 3y) = 3 * (3x – y) + 5 ⇒ I. 10x – 18y = -10 II. 4 * (3x – 4y) = 2 * (x + y) – 10 ⇒ II. -5x + 9y = 5 /*2 ⇒ -10x +18y = 10

I. + II. ⇒ 0 = 0 ⇒ Minden x és y értékre igaz.

I. 4x – 2y + z =15
II. -x + 3y + 4z =15
III. 5x – y + 3z = 26

MEGOLDÁS

I. 2x – 3y + z = 10
II. x + y – 2z = -6
III. 3y – y – 4z = -5

MEGOLDÁS

I. x + y +z =1
II. 17x + y – 7z = 9
III. 4x + 2y + z = 3

MEGOLDÁS

I. 3y – z = 7
II. 2x – 3y + 2z = -21
III. 3x + y = -21

MEGOLDÁS

I. 2x + 7y – z = 13
II. 17x – 3y + 4z = -9
III. 3x – 2y + z = -5

MEGOLDÁS

I. 3x – 4y – 6z = 42
II. -x – 2y + 3z = -6
III. 7x + 10y + 6z = 0

MEGOLDÁS

Previous Fontosabb függvények primitív függvényei

Next Primitív függvények (Határozatlan integrál)

KAPCSOLÓDÓ BEJEGYZÉSEK

Feladatok integrálszámítás

Feladatok függvényvizsgálathoz

Feladatok függvényekhez

11 hozzászólás

Kedves Tudománypláza!
“Írd fel a következő polinomokat egész számokkal szorzatalakba!” feladatok megoldási gondolatmenetét nem értem. Különösen az e,f,g,h … �� Segítenének?
Köszönöm

köszi a feladatokat.

A 3. feladatcsoport szöveges feladatokból a 3. hibásan van leírva, a szöveg elejéről kimaradt az “egy szám felének” rész.

Köszönjük a jelzést, javítottuk!

Szeretném kérni az egyes feladat csoport és a hármas feladat csoport levezetését

Hogy jobban megértse. Az általános iskolás kislányomnak kellene

3(x-1)=5(x+1)
15(4x+1)=25(2x-3)
3(2+x)-4=2(2+x)
7(x+1)-3=3(x-1)+3
6(x-2)+1=3(x+4)+1
4(3x-1)+11=2(3x-1)-9
2(3-2x)+10=5(x-3)-5
8(2-3x)-11=7(3x-2)+10
72-2(3x+1)=4(3-2x)
a levezetését is szeretném kérni hogy meg értsem köszönöm

Kedves hozzászóló! Ezek melyik feladatban vannak?

2. feladatcsoport, c feladat megoldása hibás. ( jó : -(50/3) )

Dezső! Igen-igen gyorsan javítottuk.

Leave a reply Kilépés a válaszból

LEGTÖBB HOZZÁSZÓLÁS

Algebra feladatok

Feladatok és megoldások deriválás témakörben

Tudósok, akik szerint van bizonyíték Isten létezésére

Szöveges feladatok és megoldások

Egyenletek – feladatok és megoldások

LEGOLVASOTTABB CIKKEINK

A Quercetin (kvercetin) és a D-vitamin – Szövetségesek a koronavírus ellen?

Kéz-láb-száj vírus – az új gyerekbetegség

Boldogságunk négy forrása: dopamin, endorfin, szerotonin és oxitocin

Agyérkatasztrófák nyomában

A lekopogás babonája

LEGUTÓBBI HOZZÁSZÓLÁSOK

Valcsicsák Zoltán – A Big Mac-index – szemléltethető közgazdaságtan

Kati – Szélsőérték-számítási feladatok

Hargitai Ferenc – Vicces matematika

TudományPláza – Szélsőérték-számítási feladatok

TudományPláza – Boldogságunk négy forrása: dopamin, endorfin, szerotonin és oxitocin

Egészség és életmód

Élővilág

Évezredek

Környezet

Mi magyarok

Mindennapok

Technika

Univerzum

RÓLUNK – TUDOMÁNYPLÁZA

Világunk összes titkát bizonyára sohasem fogjuk megismerni, így mindig érhetnek bennünket meglepetések. A TudományPláza egy olyan online magazin, amely igyekszik mindenki számára elérhetővé és érthetővé tenni a tényeket. Ám, nem szabad elfelejtenünk, hogy minél többet tudunk, annál kevesebbet ismerünk ahhoz képest, amit ismerni szeretnénk.

LEGUTÓBBI TUDOMÁNYOS CIKKEK

Kutatók éjszakája 2022. szeptember 30.- október 1.

Márton-napi kvíz – Ismered ezeket a babonákat?

A méhek nem csak a színeket figyelik a virágok megtalálásához

Hogyan válasszunk gyerekforgószéket?

Videó, ÉRDEKESSÉGEK

Don’t miss

Kutatók éjszakája 2022. szeptember 30.- október 1.

Márton-napi kvíz – Ismered ezeket a babonákat?

A méhek nem csak a színeket figyelik a virágok megtalálásához

Azért, hogy megkönnyítsük látogatóink számára a weboldal használatát, oldalunk cookie-kat, ismert nevén sütiket használ.
Weboldalunk böngészésével Ön beleegyezik, hogy a számítógépén, illetve mobil eszközén cookie-kat tároljunk. Elfogadom Információ

Privacy Overview

This website uses cookies to improve your experience while you navigate through the website. Out of these, the cookies that are categorized as necessary are stored on your browser as they are essential for the working of basic functionalities of the website. We also use third-party cookies that help us analyze and understand how you use this website. These cookies will be stored in your browser only with your consent. You also have the option to opt-out of these cookies. But opting out of some of these cookies may affect your browsing experience.

Necessary cookies are absolutely essential for the website to function properly. This category only includes cookies that ensures basic functionalities and security features of the website. These cookies do not store any personal information.

Any cookies that may not be particularly necessary for the website to function and is used specifically to collect user personal data via analytics, ads, other embedded contents are termed as non-necessary cookies. It is mandatory to procure user consent prior to running these cookies on your website.

Related posts:

Fizika 7 osztály tankönyv megoldások

Fizika tankönyv 2020

Mozaik kiadó tankönyv rendelés

Tankönyvkiadó bolt