2011 Május Emelt Angol Érettségi

I. Gazdaság, gazdaságpolitika, anyagi kultúra pénzügyi és gazdasági ismeretek. 1. A nagy földrajzi felfedezések. 2. Az ipari forradalom.

MATEMATIKA ÉRETTSÉGI május 3. KÖZÉPSZINT

1 MATMATIKA ÉRTTSÉGI 011. május 3. KÖZÉPSZINT 1) gyszerűsítse a következő törtet, ahol b 6 b b 36 6 I. Az egyszerűsítés utáni alak: b 6 Összesen: pont ) A, 4 és 5 számjegyek mindegyikének felhasználásával elkészítjük az összes, különböző számjegyekből álló háromjegyű számot. zek közül véletlenszerűen kiválasztunk egyet. Mennyi annak a valószínűsége, hogy az így kiválasztott szám páratlan? Válaszát indokolja! (3 pont) (A képezhető háromjegyű számok száma:) zek közül páratlan. Így a keresett valószínűség ! 6. Összesen: 3 pont 3) Hányszorosára nő egy kocka térfogata, ha minden élét háromszorosára növeljük? A kocka térfogata 7-szeresére nő ) Adottak a következő számok: a és b. Írja fel a és b legnagyobb közös osztóját és legkisebb közös többszörösét! A kért számokat elegendő prímtényezős alakban megadni. A legnagyobb közös osztó: 3 A legkisebb közös többszörös: Összesen: pont

2 5) A következő két függvény mindegyikét a valós számok halmazán értelmezzük: ;. Adja meg mindkét függvény értékkészletét! 3sin f x x f értékkészlete: g értékkészlete: sin3 g x R f Rg 33 ; 11 ; x Összesen: pont 6) Mekkora az x 6, 5x 3, 50 egyenlet valós gyökeinek összege, illetve szorzata? Válaszát indokolja! (3 pont) Az egyenlet gyökei: 7 és 0,5. A gyökök összege: 6,5. A gyökök szorzata: 3,5. Összesen: 3 pont 7) Az A halmaz az 5-re végződő kétjegyű pozitív egészek halmaza, a B halmaz pedig a kilenccel osztható kétjegyű pozitív egészek halmaza. Adja meg elemeik felsorolásával az alábbi halmazokat: (4 pont) A; B; A B; A\ B; A 15;5;35;45;55;65;75;85;95 B 18;7;36;45;54;63;7;81;90;99 AB 45 A\ B 15;5;35;55;65;75;85;95 8) Adja meg az alábbi két egyenlet valós gyökeit! a) b) x y 5 x Összesen: 4 pont 5 65 y 1 3 Összesen: pont

3 9) Melyik szám nagyobb? 1 A lg 10 vagy B cos8 cos 8 A nagyobb szám betűjele: B 10) Oldja meg a valós számok halmazán a következő egyenletet! x 7 Az egyenlet megoldása a 9 és a 5. Összesen: pont 11) Melyik a 01-edik pozitív páros szám? Válaszát indokolja! (3 pont) Az a 1 első tagú, a d differenciájú számtani sorozat felismerése. Összesen: 3 pont 1) Döntse el az alábbi állítások mindegyikéről, hogy igaz-e vagy hamis! A: Ha két szám négyzete egyenlő, akkor a számok is egyenlők. B: A kettes számrendszerben felírt szám a tízes számrendszerben 0. C: gy hat oldalú konvex sokszögnek 6 átlója van. A: hamis B: igaz C: hamis Összesen: 3 pont

4 II/A. 13) gy iskolai tanulmányi verseny döntőjébe 30 diák jutott be, két feladatot kellett megoldaniuk. A verseny után a szervezők az alábbi oszlopdiagramokon ábrázolták az egyes feladatokban szerzett pontszámok eloszlását: a) A diagramok alapján töltse ki a táblázat üres mezőit! Az első feladatra kapott pontszámok átlagát két tizedes jegyre kerekítve adja meg! (3 pont) 1. feladat. feladat pontszámok átlaga 3,10 pontszámok mediánja b) A megfelelő középponti szögek megadása után ábrázolja kördiagramon a. feladatra kapott pontszámok eloszlását! (4 pont) c) A versenyen minden tanuló elért legalább 3 pontot. Legfeljebb hány olyan tanuló lehetett a versenyzők között, aki a két feladat megoldása során összesen pontosan 3 pontot szerzett? (5 pont)

5 a) 1. feladat. feladat pontszámok átlaga 3,57 3,10 pontszámok mediánja 3,5 4 (3 pont) b) gy tanulóhoz tartozó középponti szög: tanulóhoz 156, 6 tanulóhoz 7, 4 tanulóhoz 48, 3 tanulóhoz 36, tanulóhoz 4 tartozik. c) gy tanuló 3 pontot négyféleképpen érhetne el: 0 3; 1 ; 1; 3 0. A diagram alapján nem valósulhat meg: 0 3; 1. 1 pontot 1 tanuló kaphatott. 3 0 pontot tanuló kaphatott. Legfeljebb 3 tanuló érhetett el pontosan 3 pontot. Összesen: 1 pont 14) gy autó ára újonnan millió 15 ezer forint, a megvásárlása után öt évvel ennek az autónak az értéke 900 ezer forint. a) A megvásárolt autó tulajdonosának a vezetési biztonságát a vásárláskor 90 ponttal jellemezhetjük. z a vezetési biztonság évente az előző évinek 6 %-ával nő. (4 pont) Hány pontos lesz 5 év elteltével az autótulajdonos vezetési biztonsága? Válaszát egész pontra kerekítve adja meg! b) Az első öt év során ennek az autónak az értéke minden évben az előző évi értékének ugyanannyi százalékával csökken. Hány százalék ez az éves csökkenés? (8 pont) Válaszát egész százalékra kerekítve adja meg!

6 a) A vezetési biztonság pontjai egy tagjai. (bben a sorozatban) 5 t ,06 t (pont)., q 1,6 hányadosú mértani sorozat 90 1,06 10,44 tehát 5 év után a vezetési biztonság 10 pontos. b) Legyen a csökkenési ráta x. 5 kkor,15 x 0, x 15 0,418, amiből x , x 0,84 10,84 0,16, tehát évente 16 %-kal csökken az autó értéke. A feladat megoldható úgy is, ha a kamatos kamatszámításhoz hasonló képletet használunk. Összesen: 1 pont 15) Az ABC háromszög csúcsainak koordinátái:, és. a) Számítsa ki az ABC háromszög szögeit! (5 pont) b) Írja fel az ABC háromszög körülírt körének egyenletét! (7 pont) A 3; B 3 ; C 00 ; a) Az ABC háromszög egyenlő szárú. Az AB alapon fekvő hegyesszögek tangense 3 tehát az alapon fekvő szögek nagysága 33,7, a szárak szöge pedig 11,6. b) A körülírt kör középpontja az oldalfelező merőlegesek közös pontja, ez a szimmetria miatt az ordinátatengelyen van. felezőponton. 1,5;1 Az AC oldal felezőmerőlegese átmegy a Az AC oldal felezőmerőlegesének egy normálvektora a CA, CA3;. Az AC oldal felezőmerőlegesének egyenlete:. z az y tengelyt a 0;3,5 pontban metszi (ez a körülírt kör középpontja). A kör sugara 3,5. 3x y 6,5 A körülírt kör egyenlete: x y 3,5 3,5. Összesen: 1 pont

7 II/B. 16) gy 1 cm oldalhosszúságú négyzetet megforgatunk az egyik oldalával párhuzamos szimmetriatengelye körül. a) Mekkora az így keletkező forgástest térfogata és felszíne? (6 pont) A felszínt egész cm -re, a térfogatot egész cm 3 -re kerekítve adja meg! Ugyanezt a négyzetet forgassuk meg az egyik átlóját tartalmazó forgástengely körül! b) Mekkora az így keletkező forgástest térfogata és felszíne? (9 pont) A felszínt egész cm -re, a térfogatot egész cm 3 -re kerekítve adja meg! c) A forgástestek közül az utóbbinak a felszíne hány százaléka az első forgatással kapott forgástest felszínének? a) Az első esetben a forgástengely a négyzet szemközti oldalainak közös felezőmerőlegese, a keletkező forgástest forgáshenger: alapkörének sugara 6 cm, magassága 1 cm. Térfogata: V 1 43 V cm 3 Felszíne: A A cm b) A második esetben (mivel a négyzet átlói merőlegesen felezik egymást) a forgástest egy kettőskúp. A közös köralap átmérője a négyzet átlója, a kúpok magassága a négyzet átlóhosszának fele. d 1 17 A négyzet átlója: 6 6 Az egyik kúp térfogata: V 1 3 azaz V V V A két kúp egybevágó, így a kettőskúp térfogata: A forgáskúp palástja kiterítve körcikk, amelynek az ívhossza ,4 cm cm sugara 1 cm hosszú. Így a területe: cm T A kettőskúp felszíne: cm c) A kérdezett százalék: azaz kb. 94%. T T A 1 16, Összesen: 17 pont

8 17) gy új típusú, az alacsonyabb nyomások mérésére kifejlesztett műszer tesztelése során azt tapasztalták, hogy a műszer által mért pm és a valódi pv nyomás között a lg 0,8 lg 0,301 összefüggés áll fenn. A műszer által mért és a valódi nyomás egyaránt pascal (Pa) egységekben szerepel a képletben. a) Mennyit mér az új műszer 0 Pa valódi nyomás esetén? (4 pont) b) Mennyi valójában a nyomás, ha a műszer 50 Pa értéket mutat?(6 pont) c) Mekkora nyomás esetén mutatja a műszer a valódi nyomást? (7 pont) A pascalban kiszámított értékeket egész számra kerekítve adja meg! a) b) c) lg p m 0,8 lg 0 0,301 lg p m 1,34 pm Pa lg 50 0,8 lg 0,301 lg p v p v lg 50 0,301 0,8 lg 1,747 pv p v p v 56 Pa p m felismerése p m p v, (Legyen a keresett nyomás ), lg p 0,8 lg p 0,301 0,301 lg p 1,505 0, p 3 Pa p p p v m Összesen: 17 pont

9 18) András, Balázs, Cili, Dóra és nikő elhatározták, hogy sorsolással döntenek arról, hogy közülük ki kinek készít ajándékot. Úgy tervezték, hogy a neveket ráírják egy-egy papírcetlire, majd a lefelé fordított öt cédulát összekeverik, végül egy sorban egymás mellé leteszik azokat az asztalra. zután, keresztnevük szerinti névsorban haladva egymás után vesznek el egy-egy cédulát úgy, hogy a soron következő mindig a bal szélső cédulát veszi el. a) Mennyi a valószínűsége, hogy az elsőnek húzó Andrásnak a saját neve jut? (5 pont) b) Írja be az alábbi táblázatba az összes olyan sorsolás eredményét, amelyben csak nikőnek jut a saját neve! A táblázat egyes soraiban az asztalon lévő cédulák megfelelő sorrendjét adja meg! (A megadott táblázat sorainak a száma lehet több, kevesebb vagy ugyanannyi, mint a felsorolandó esetek száma. nnek megfelelően hagyja üresen a felesleges mezőket, vagy egészítse ki újabb mezőkkel a táblázatot, ha szükséges!) (6 pont) A húzó neve A B C D A cédulák megfelelő sorrendjei c) Az ajándékok átadása után mind az öten moziba mentek, és a nézőtéren egymás mellett foglaltak helyet. Hány különböző módon kerülhetett erre sor, ha tudjuk, hogy a két fiú nem ült egymás mellett? (6 pont) a) Az 5 név bármelyike ugyanakkora valószínűséggel kerülhet az első helyre, 1 tehát a keresett valószínűség 0,. 5 A feladat megoldható a kedvező/összes formulával is.

10 b) A húzó neve A B C D B A D C B C D A A cédulák megfelelő sorrendjei B D A C C A D B C D A B C D B A D A B C D C A B D C B A (6 pont) c) Azt a két helyet, ahol a fiúk ülhetnek (nem egymás mellett), 6-féleképpen választhatjuk ki, 5 mert 4 6. A két kiválasztott helyen a fiúk -féleképpen helyezkedhetnek el. A lányok minden egyes esetben egymáshoz képest. Összesen tehát 7 különböző módon ülhetnek le. Komplementer halmazzal is számolhatunk. Összesen: 17 pont 6 6 3! 6 különböző módon ülhetnek le

2011 Május Emelt Angol Érettségi

00 matematika idegen nyelven történelem 2011. május 4. 00 történelem idegen nyelven angol nyelv 2011. május 5. 00 német nyelv 2011. május 6. 00 horvát nyelv és irodalom 2011. május 9. 00 német nemzetiségi nyelv és irodalom német nemzetiségi nyelv román nyelv és irodalom szerb nyelv és irodalom szlovák nyelv és irodalom szlovén nemzetiségi nyelv latin nyelv 2011. május 10. – 14. 00 héber nyelv biológia 2011. május 11. 00 biológia idegen nyelven kémia 2011. május 12. 00 kémia idegen nyelven földrajz 2011. 00 földrajz idegen nyelven egészségügyi alapismeretek 2011. május 13.

2011 május emelt angol érettségi yakorlo feladatok

Elhunyt Libero De Rienzo színész-rendező Régen láttuk őket: Óriási változott a kicsi Venci, Mici pedig kész nagylány. Ördög Nóráék nyaralási fotói fantasztikusak Kiskegyed – AKCIÓK Megjelent a legújabb Kiskegyed Konyhája (X) Játssz a Kiskegyeddel, és nyerj akár 500 ezer forintot! (X) Diétás, fogyókúrás receptekkel megjelent a Kiskegyed Konyhája különszáma! (X) FRISS HÍREK 20:02 19:34 19:06 19:03

A tanárok megfelelő nehézségűnek találták a 2011-es angolérettségit, amelyben utazásos témák és anekdoták is voltak. A 180 perces középszintű vizsgát 58 521-en, a négyórás emeltet pedig 6 194-en töltötték ki. a rovat legfrissebb cikkei

2011 május emelt angol érettségi zokincs

A kapott értéket behelyettesítette a képletbe és 3, 1596 jött ki neki. Természetesen “végtelen számú” feldobás hozna pontos közelítést, de ha figyelembe vesszük, hogy egyszerű tűdobálással számította ki ezt az értéket…

2011 május emelt angol érettségi raskeszseg

2011. ápr 27. 0:00 #gimnázium #érettségi #2011 #vizsga 30001_erettsegi-240-d000269C0637464aec219 Május első hetén kezdődnek az idei érettségi vizsgák, amik egészen június végéig elhúzódhatnak. Íme az időpontok! Írásbeli érettségi időpontok 1. magyar nyelv és irodalom emelt szintű, magyar nyelv és irodalom, magyar mint idegen nyelv középszintű érettségi: 2011. május 2., 8. 002. matematika emelt-, és középszintű érettségi: 2011. május 3., 8. 003. történelem emelt-, és középszintű érettségi: 2011. május 4., 8. 004. angol nyelv emelt-, és középszintű érettségi: 2011. május 5., 8. 005. német nyelv emelt-, és középszintű érettségi: 2011. május 6., 8. 006. nemzetiségi nyelv és irodalom, nemzetiségi nyelv emelt-, és középszintű érettségi: 2011. május9., 8. 007. informatika emelt szintű érettségi: 2011. május 10., 8. 008. latin nyelv, héber nyelv emelt-, és középszintű érettségi: 2011. május 10., 14. 009. biológia emelt-, és középszintű érettségi: 2011. május 11., 8. 00 10. társadalomismeret emelt szintű érettségi: 2011. május 11., 14.

2011 május emelt angol érettségi 016

2011. 09:11 Angolérettségi: feladatok és megoldások elsőként itt! Nyolc órakor megkezdődött az angolérettségi: folyamatosan figyelemmel követjük az eseményeket, hogy ne maradj le semmilyen fontos infóról, a középszintű írásbeli feladatait és a nem hivatalos megoldásokat pedig 13 órakor nézheted át. 2011. 06:42 Nyolckor kezdődik az angolérettségi: több mint 60 ezren vizsgáznak Az angol írásbelikkel folytatódnak ma reggel 8 órakor a tavaszi érettségi vizsgák, a diákok közép- és emelt szinten adnak számot tudásukról. Középszinten 1 187 helyszínen 58 521-en, emelt szinten 88 helyszínen 6 194-en vizsgáznak ebből a tárgyból. 2011. 04. 21:05 Angolérettségi: milyen az idei feladatsor? Csütörtökön az angol írásbelivel folytatódik az érettségi időszak: középszinten 58 521-en, emelt szinten 6 194-en vizsgáznak. A vizsga után a középszintű feladatlapokat és a nem hivatalos megoldásokat is megtaláljátok az eduline-on.

1. Az ember, aki mindent tudott – Wikipédia
2. Móra ferenc a cinege cipője vers
3. Arany női fülbevaló francia kapcsos
4. Egészségügyi szolgáltatások: Komárom-Esztergom megye, Közép-Dunántúl
5. Eduline.hu – angol érettségi 2011
6. 2011 május emelt angol érettségi inta
7. Érettségi eredmények
8. 2011 május emelt angol érettségi yakorlo feladatok
9. Eladó panel lakás – Pest megye, Gödöllő, Szent János utca #32287385

2011 május emelt angol érettségi 013

MÁJUS-JÚNIUS Előrehozott érettségi vizsgák 5. 00 3. 48 4. 50 4. 66 4. 5 Az első 5 éves nyelvi előkészítő osztályunk a rendszer sajátosságából adódóan 2009-ben tett rendes érettségi vizsgát.

00 informatika idegen nyelven ábrázoló és művészeti geometria 2011. 00 ének-zene művészettörténet fizika 2011. május 17. 00 fizika idegen nyelven rajz és vizuális kultúra 2011. 00 francia nyelv 2011. május 18. 00 filozófia 2011. 00 olasz nyelv 2011. május 19. 00 dráma 2011. 00 mozgóképkultúra és médiaismeret spanyol nyelv 2011. május 20. 00 arab nyelv 2011. május 23. 00 beás nyelv bolgár nyelv eszperantó nyelv finn nyelv holland nyelv horvát nyelv japán nyelv kínai nyelv lengyel nyelv lovári nyelv orosz nyelv portugál nyelv román nyelv szerb nyelv szlovák nyelv újgörög nyelv ukrán nyelv belügyi rendészeti ismeretek 2011. 00 katonai alapismeretek természettudomány

Érettségi-felvételi 2012. április. 13. 18:12 Mennyire tudsz angolul? Teszteld, hány pontot érnél el az érettségin Több mint 58 ezren választották angolból a középszintű érettségit 2011 májusában, emelt szinten csupán 6194-en vizsgáztak. Kevesebb mint egy hónap van hátra az angolérettségiig – ha már nem bírtok magatokkal, töltsétek le az előző évek feladatsorait, és nézzétek meg, most hány pontot szereznétek. Eduline 2011. október. 21. 13:04 Itt van az emelt szintű angolérettségi feladasora és megoldókulcsa A középszintű angolérettségi feladatsora és megoldókulcsa után az emelt szintű vizsga tesztlapját is közzétette az. 2011. június. 11. 07:54 Ilyen a szóbeli angolérettségi: kidolgozott tételek és feladattípusok Június 14-én kezdődik a középszintű szóbeli érettségi, angolból több mint 58 ezren vizsgáznak. Az idegen nyelvi szóbeli három részből áll: a rövid, bevezető kérdések után egy szituációs játék következik, végül egy hétköznapi témáról kell két-három percig beszélni. 2011. május.

-ben a szintén angol Fergusson kimutatta, hogy az 528. Tizedestől kezdve tévedett… Már a XVIII. századtól tudták, hogy irracionális szám, jelölésére a görög “Pi” betűt 1739. -ben Euler javasolta. Most pedig nézzük, hogy mi is kötődik Buffon gróf nevéhez? A legenda szerint felesége rendszeresen kötögetett, és gyakran kiesett a kezéből a kötőtű. Padlójukat, párhuzamosan lefektetett deszkalapok borították, ezért a leeső tű néha metszette, néha pedig nem metszette, a padlólapok illesztéseinél látható vonalakat. Állítólag ez késztette Buffon grófot arra, hogy 1777. -ben, elsőként bevezesse a geometriai valószínűség fogalmát. Képletben adta meg, hogy mi a valószínűsége annak, hogy a leeső tű metszi a padló vonalát (ez nyílván függ a vonalak távolságától, és a tű hosszától, és szerepel benne a Pi, értéke is). A zürichi Rudolf Wolf 1850. -ben a képletet átrendezte, Pi értékére. A vonalak távolsága 45 mm volt, 35 mm-es tűt használt, amit 5000 szer dobott fel, és számolta, hogy hányszor metszi a vonalak egyikét.

Matematika érettségi 2011 május megoldás

Mai 1144
Heti 9138
Havi 31554
Összes 4003220
IP: 104.28.222.237 Chrome – Windows 2022. október 14. péntek, 08:43

Ki van itt?

Honlapok

SULINET Matematika

Oktatási Hivatal

Versenyvizsga portál

Matematika Portálok

Berzsenyi Dániel Gimnázium


Óbudai Árpád Gimnázium


Szent István Gimnázium

A gondolkodás öröme

251. találat: Matematika középszintű érettségi, 2010. október, I. rész, 9. feladat
Témakör: *Algebra (Azonosító: mmk_201010_1r09f )

A $ b $, $ c $ és $ d $ pozitív számokat jelölnek. Tudjuk, hogy $ \lg b = \dfrac<\lg c-\lg d>3 $ Fejezze ki az egyenlőségből $ b $-t úgy, hogy abban $ c $ és $ d $ logaritmusa ne szerepeljen!

252. találat: Matematika középszintű érettségi, 2010. október, I. rész, 10. feladat
Témakör: *Algebra (Azonosító: mmk_201010_1r10f )

Adja meg képlettel egy olyan, a valós számok halmazán értelmezett függvény hozzárendelési utasítását, amelynek (abszolút) maximuma van! A megadott függvénynek állapítsa meg a maximumhelyét is!

253. találat: Matematika középszintű érettségi, 2010. október, I. rész, 11. feladat
Témakör: *Kombinatorika (Azonosító: mmk_201010_1r11f )

A diákönkormányzat újonnan választott négytagú vezetősége: Kata, Mari, Réka és Bence. Közülük Kata három, Réka és Bence pedig két-két vezetőségi tagot ismert korábbról. Mari a négyes csoportnak csak egy tagját ismerte. (Az ismeretségek kölcsönösek.) Rajzolja fel a négytagú vezetőség választás előtti ismeretségi gráfját!

254. találat: Matematika középszintű érettségi, 2010. október, I. rész, 12. feladat
Témakör: *Algebra (Azonosító: mmk_201010_1r12f )

Egy kör az $ (1; 0) $ és $ (7; 0) $ pontokban metszi az x tengelyt. Tudjuk, hogy a kör középpontja az $ y = x $ egyenletű egyenesre illeszkedik. Írja fel a kör középpontjának koordinátáit! Válaszát indokolja!

255. találat: Matematika középszintű érettségi, 2010. október, II. rész, 13. feladat
Témakör: *Algebra (Azonosító: mmk_201010_2r13f )

Oldja meg a valós számok halmazán a következő egyenlőtlenségeket!

a) $ x-\dfrac 2 > \dfrac 4 – \dfrac 3 $

Mindkét esetben ábrázolja a megoldáshalmazt számegyenesen!

256. találat: Matematika középszintű érettségi, 2010. október, II. rész, 14. feladat
Témakör: *Geometria (Azonosító: mmk_201010_2r14f )

Az iskolatejet gúla alakú, impregnált papírból készült dobozba csomagolják. (Lásd az alábbi ábrát, ahol $ CA = CB = CD $ .)

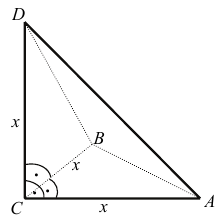
A dobozba 2,88 dl tej fér.

a) Számítsa ki a gúla éleinek hosszát! Válaszát egész $ cm $-ben adja meg!

b) Mekkora a papírdoboz felszíne? Válaszát $ cm^2 $-ben, egészre kerekítve adja meg!

257. találat: Matematika középszintű érettségi, 2010. október, II. rész, 15. feladat
Témakör: *Kombinatorika (Azonosító: mmk_201010_2r15f )

Egy kockajátékban egy menet abból áll, hogy szabályos dobókockával kétszer dobunk egymás után. Egy dobás 1 pontot ér, ha négyest, vagy ötöst dobunk, egyébként a dobásért nem jár pont. A menetet úgy pontozzák, hogy a két dobásért járó pontszámot összeadják.

a) Mennyi annak a valószínűsége, hogy egy menetben 1 pontot szerzünk, és azt az első dobásért kapjuk?

b) Minek nagyobb a valószínűsége,

– annak, hogy egy menetben szerzünk pontot, vagy

– annak, hogy egy menetben nem szerzünk pontot?

258. találat: Matematika középszintű érettségi, 2010. október, II. rész, 16. feladat
Témakör: *Algebra (Azonosító: mmk_201010_2r16f )

a) Egy számtani sorozat első tagja -7, a nyolcadik tagja 14. Adja meg n lehetséges értékeit, ha a sorozat első n tagjának összege legfeljebb 660.

b) Egy mértani sorozat első tagja ugyancsak -7, a negyedik tagja -189. Mekkora az n, ha az első n tag összege -68 887?

259. találat: Matematika középszintű érettségi, 2010. október, II. rész, 17. feladat
Témakör: *Geometria (Azonosító: mmk_201010_2r17f )

Az ábrán egy ejtőernyős klub kitűzője látható. (Az egyik körív középpontja a szabályos háromszög A csúcsa, a másik körív középpontja az A csúccsal szemközti oldal felezőpontja.) Ezt a lapot fogják tartományonként színesre festeni.

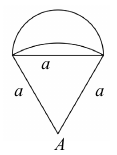
a) A Számítsa ki egyenként mindhárom tartomány területét, ha a = 2,5 cm ! Számításait legalább két tizedesjegy pontossággal végezze, és az így kapott eredményt egy tizedesjegyre kerekítve adja meg!

b) Hányféle módon festhető színesre a kitűző, ha minden tartományt a piros, sárga, zöld és kék színek valamelyikére festenek a következő két feltétel együttes figyelembe vételével:

(1) szomszédos tartományok nem lehetnek azonos színűek;

(2) piros és sárga színű tartomány nem lehet egymás mellett. (Szomszédos tartományoknak van közös határvonala.)

260. találat: Matematika középszintű érettségi, 2010. október, II. rész, 18. feladat
Témakör: *Kombinatorika (Azonosító: mmk_201010_2r18f )

Megkérdeztek 25 családot arról, hogy hány forintot költöttek az elmúlt hónapban friss gyümölcsre. A felmérés eredményét mutatja az alábbi táblázat:

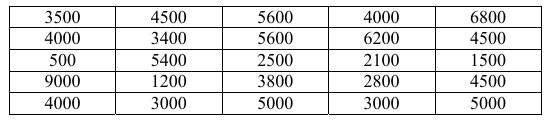
(Az adatokat tekintsük pontos értékeknek!)

a) Hány forintot költöttek átlagosan ezek a családok friss gyümölcs vásárlására az elmúlt hónapban?

b) Ossza 1000 Ft terjedelmű osztályokba a fenti értékeket, kezdve a 0-1000 Ft, 1001-2000 Ft stb. osztályokkal, és ábrázolja ezeknek az osztályoknak a gyakoriságát oszlopdiagramon!

c) Az 500 Ft és a 9000 Ft kiugró értékek. Mennyi a megmaradt adatok átlaga, ha ezeket a kiugró értékeket elhagyjuk az adatok közül? Hány százalékos változást jelent ez az eredeti átlaghoz képest, és milyen irányú ez a változás? Mennyi az így keletkezett új adatsor terjedelme?

(Azátlagot forintra, a százaléklábat két tizedesjegyre kerekítve adja meg!)

d) Az eredeti mintát a vizsgálatot végző cég két új család megfelelő adatával bővítette. Az egyik az eredeti átlagnál 1000 Ft-tal többet, a másik ugyanennyivel kevesebbet költött havonta friss gyümölcsre. Mutassa meg számítással, hogy így az átlag nem változott!

261. találat: Matematika középszintű érettségi, 2011. május, I. rész, 1. feladat
Témakör: *Algebra ( nevezetes azonosság, egyszerűsítés) (Azonosító: mmk_201105_1r01f )

Egyszerűsítse a következő törtet, ahol $b \neq 6$.

262. találat: Matematika középszintű érettségi, 2011. május, I. rész, 2. feladat
Témakör: *Valószínűségszámítás ( kombinatorika) (Azonosító: mmk_201105_1r02f )

A 2, 4 és 5 számjegyek mindegyikének felhasználásával elkészítjük az összes, különböző számjegyekből álló háromjegyű számot. Ezek közül véletlenszerűen kiválasztunk egyet. Mennyi annak a valószínűsége, hogy az így kiválasztott szám páratlan? Válaszát indokolja!

263. találat: Matematika középszintű érettségi, 2011. május, I. rész, 3. feladat
Témakör: *Térgeometria ( hasonlóság) (Azonosító: mmk_201105_1r03f )

Hányszorosára nő egy kocka térfogata, ha minden élét háromszorosára növeljük?

264. találat: Matematika középszintű érettségi, 2011. május, I. rész, 4. feladat
Témakör: *Oszthatóság ( számelmélet, LNKO, LKKT) (Azonosító: mmk_201105_1r04f )

Adottak a következő számok: $a=2^3 \cdot 5 \cdot 7^2 \cdot 11^4$ és $b=2 \cdot 5^2 \cdot 11^3 \cdot 15$. Írja fel a és b legnagyobb közös osztóját és legkisebb közös többszörösét! A kért számokat elegendő prímtényezős alakban megadni.

265. találat: Matematika középszintű érettségi, 2011. május, I. rész, 5. feladat
Témakör: *Függvények ( trigonometria) (Azonosító: mmk_201105_1r05f )

A következő két függvény mindegyikét a valós számok halmazán értelmezzük: $f(x)= \sin x; \quad g(x)=\sin 3x$. Adja meg mindkét függvény értékkészletét!

266. találat: Matematika középszintű érettségi, 2011. május, I. rész, 6. feladat
Témakör: *Algebra ( másodfokú) (Azonosító: mmk_201105_1r06f )

Mekkora az $x^2-6,5x-3,5=0$ egyenlet valós gyökeinek összege, illetve szorzata? Válaszát indokolja!

267. találat: Matematika középszintű érettségi, 2011. május, I. rész, 7. feladat
Témakör: *Halmazok ( metszet, különbség) (Azonosító: mmk_201105_1r07f )

Az A halmaz az 5-re végződő kétjegyű pozitív egészek halmaza, a B halmaz pedig a kilenccel osztható kétjegyű pozitív egészek halmaza. Adja meg elemeik felsorolásával az alábbi halmazokat:

$A; \quad B; \quad A \cap B; \quad A \setminus B$

268. találat: Matematika középszintű érettségi, 2011. május, I. rész, 8. feladat
Témakör: *Algebra ( exponenciális) (Azonosító: mmk_201105_1r08f )

Adja meg az alábbi két egyenlet valós gyökeit!

a) $ 5^=625$

b) $ 2^y = \dfrac$

269. találat: Matematika középszintű érettségi, 2011. május, I. rész, 9. feladat
Témakör: *Algebra ( logaritmus, trigonometria) (Azonosító: mmk_201105_1r09f )

Melyik szám nagyobb?

$A= \lg \dfrac$ vagy $B=\cos 8\pi$

270. találat: Matematika középszintű érettségi, 2011. május, I. rész, 10. feladat
Témakör: *Algebra ( abszolútérték) (Azonosító: mmk_201105_1r10f )

Oldja meg a valós számok halmazán a következő egyenletet!

271. találat: Matematika középszintű érettségi, 2011. május, I. rész, 11. feladat
Témakör: *Sorozatok ( algebra, számtani sorozat) (Azonosító: mmk_201105_1r11f )

Melyik a 201-edik pozitív páros szám? Válaszát indokolja!

272. találat: Matematika középszintű érettségi, 2011. május, I. rész, 12. feladat
Témakör: *Logika ( algebra, geometria) (Azonosító: mmk_201105_1r12f )

Döntse el az alábbi állítások mindegyikéről, hogy igaz-e vagy hamis!

A: Ha két szám négyzete egyenlő, akkor a számok is egyenlők.

B: A kettes számrendszerben felírt 10100 szám a tízes számrendszerben 20.

C: Egy hat oldalú konvex sokszögnek 6 átlója van.

273. találat: Matematika középszintű érettségi, 2011. május, II. rész, 13. feladat
Témakör: *statisztika (medián, átlag, diagram, grafikon) (Azonosító: mmk_201105_2r13f )

Egy iskolai tanulmányi verseny döntőjébe 30 diák jutott be, két feladatot kellett megoldaniuk. A verseny után a szervezők az alábbi oszlopdiagramokon ábrázolták az egyes feladatokban szerzett pontszámok eloszlását:

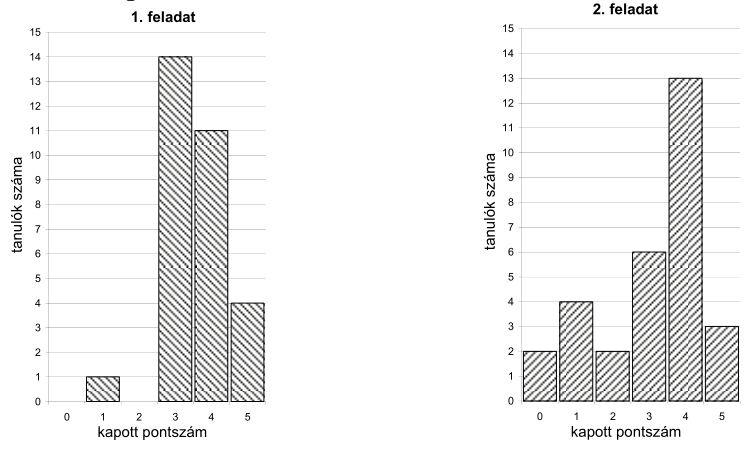
a) A diagramok alapján töltse ki a táblázat üres mezőit! Az első feladatra kapott pontszámok átlagát két tizedes jegyre kerekítve adja meg!

b) A megfelelő középponti szögek megadása után ábrázolja kördiagramon a 2. feladatra kapott pontszámok eloszlását!

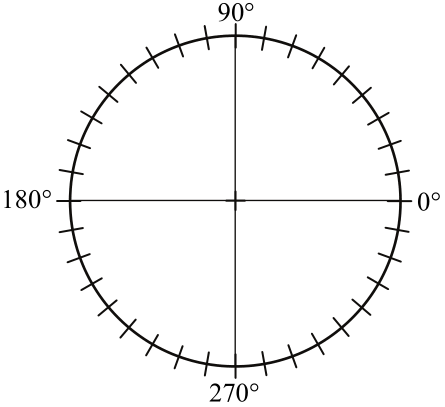
c) A versenyen minden tanuló elért legalább 3 pontot. Legfeljebb hány olyan tanuló lehetett a versenyzők között, aki a két feladat megoldása során összesen pontosan 3 pontot szerzett?

274. találat: Matematika középszintű érettségi, 2011. május, II. rész, 14. feladat
Témakör: *Sorozatok (mértani sorozat) (Azonosító: mmk_201105_2r14f )

Egy autó ára újonnan 2 millió 152 ezer forint, a megvásárlása után öt évvel ennek az autónak az értéke 900 ezer forint.

a) A megvásárolt autó tulajdonosának a vezetési biztonságát a vásárláskor 90 ponttal jellemezhetjük. Ez a vezetési biztonság évente az előző évinek 6 %-ával nő. Hány pontos lesz 5 év elteltével az autótulajdonos vezetési biztonsága? Válaszát egész pontra kerekítve adja meg!

b) Az első öt év során ennek az autónak az értéke minden évben az előző évi értékének ugyanannyi százalékával csökken. Hány százalék ez az éves csökkenés? Válaszát egész százalékra kerekítve adja meg!

275. találat: Matematika középszintű érettségi, 2011. május, II. rész, 15. feladat
Témakör: *Koordinátageometria (skaláris szorzat, koszinusztétel, egyenlő szárú, tangens) (Azonosító: mmk_201105_2r15f )

Az ABC háromszög csúcsainak koordinátái: A(-3; 2); B(3; 2); és C(0;0).

a) Számítsa ki az ABC háromszög szögeit!

b) Írja fel az ABC háromszög körülírt körének egyenletét!

276. találat: Matematika középszintű érettségi, 2011. május, II. rész, 16. feladat
Témakör: *Térgeometria (henger, kúp, kettőskúp) (Azonosító: mmk_201105_2r16f )

Egy 12 cm oldalhosszúságú négyzetet megforgatunk az egyik oldalával párhuzamos szimmetriatengelye körül.

a) Mekkora az így keletkező forgástest térfogata és felszíne? A felszínt egész $ cm^2 $-re, a térfogatot egész $ cm^3 $-re kerekítve adja meg!

Ugyanezt a négyzetet forgassuk meg az egyik átlóját tartalmazó forgástengely körül!

b) Mekkora az így keletkező forgástest térfogata és felszíne? A felszínt egész $ cm^2 $-re, a térfogatot egész $ cm^3 $-re kerekítve adja meg!

c) A forgástestek közül az utóbbinak a felszíne hány százaléka az első forgatással kapott forgástest felszínének?

277. találat: Matematika középszintű érettségi, 2011. május, II. rész, 17. feladat
Témakör: *Algebra (logaritmus, egyenlet, helyettesítési érték) (Azonosító: mmk_201105_2r17f )

Egy új típusú, az alacsonyabb nyomások mérésére kifejlesztett műszer tesztelése során azt tapasztalták, hogy a műszer által mért $ p_m $ és a valódi $ p_v $ nyomás között a $ \lg p_m=0,8 \cdot \lg p_v+0,301 $ összefüggés áll fenn. A műszer által mért és a valódi nyomás egyaránt pascal (Pa) egységekben szerepel a képletben.

a) Mennyit mér az új műszer 20 Pa valódi nyomás esetén?

b) Mennyi valójában a nyomás, ha a műszer 50 Pa értéket mutat?

c) Mekkora nyomás esetén mutatja a műszer a valódi nyomást?

A pascalban kiszámított értékeket egész számra kerekítve adja meg!

278. találat: Matematika középszintű érettségi, 2011. május, II. rész, 18. feladat
Témakör: *Kombinatorika (valószínűségszámítás) (Azonosító: mmk_201105_2r18f )

András, Balázs, Cili, Dóra és Enikő elhatározták, hogy sorsolással döntenek arról, hogy közülük ki kinek készít ajándékot. Úgy tervezték, hogy a neveket ráírják egy-egy papírcetlire, majd a lefelé fordított öt cédulát összekeverik, végül egy sorban egymás mellé leteszik azokat az asztalra. Ezután, keresztnevük szerinti névsorban haladva egymás után vesznek el egy-egy cédulát úgy, hogy a soron következő mindig a bal szélső cédulát veszi el.

a) Mennyi a valószínűsége, hogy az elsőnek húzó Andrásnak a saját neve jut?

b) Írja be az alábbi táblázatba az összes olyan sorsolás eredményét, amelyben csak Enikőnek jut a saját neve! A táblázat egyes soraiban az asztalon lévő cédulák megfelelő sorrendjét adja meg! (A megadott táblázat sorainak a száma lehet több, kevesebb vagy ugyanannyi, mint a felsorolandó esetek száma. Ennek megfelelően hagyja üresen a felesleges mezőket, vagy egészítse ki újabb mezőkkel a táblázatot, ha szükséges!)

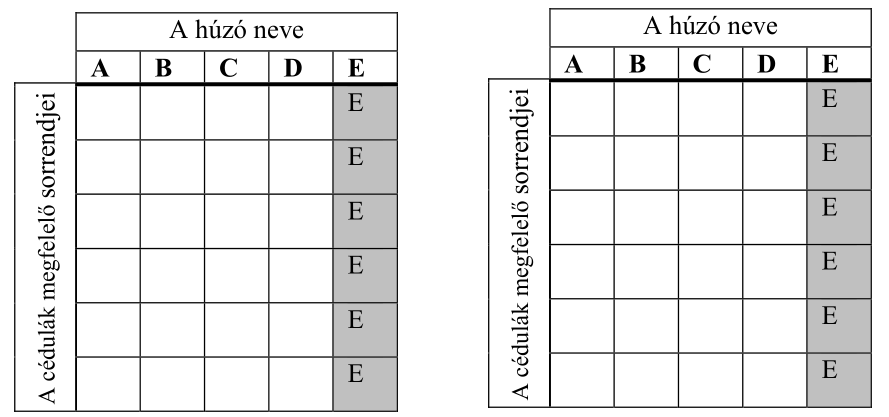
c) Az ajándékok átadása után mind az öten moziba mentek, és a nézőtéren egymás mellett foglaltak helyet. Hány különböző módon kerülhetett erre sor, ha tudjuk, hogy a két fiú nem ült egymás mellett?

279. találat: Matematika középszintű érettségi, 2011. október, I. rész, 1. feladat
Témakör: *Számelmélet ( prím) (Azonosító: mmk_201110_1r01f )

Írja fel prímszámok szorzataként a 420-at!

280. találat: Matematika középszintű érettségi, 2011. október, I. rész, 2. feladat
Témakör: *Algebra ( arány) (Azonosító: mmk_201110_1r02f )

Bontsa fel a 36 000-et két részre úgy, hogy a részek aránya 5 : 4 legyen!

281. találat: Matematika középszintű érettségi, 2011. október, I. rész, 3. feladat
Témakör: *Sorozatok ( algebra, mértani sorozat) (Azonosító: mmk_201110_1r03f )

Egy sejttenyészetben 2 naponta kétszereződik meg a sejtek száma. Az első nap kezdetén 5000 sejtből állt a tenyészet. Hány sejt lesz a tenyészetben 8 nap elteltével? Számításait részletezze!

282. találat: Matematika középszintű érettségi, 2011. október, I. rész, 4. feladat
Témakör: *Halmazok ( halmazművelet) (Azonosító: mmk_201110_1r04f )

Jelölje $\mathbb$ a természetes számok halmazát, $\mathbb$ az egész számok halmazát és $\varnothing$ az üres halmazt! Adja meg az alábbi halmazműveletek eredményét!

a) $\mathbb\cap \mathbb$

b) $\mathbb\cup \varnothing $

c) $\varnothing \setminus \mathbb$

283. találat: Matematika középszintű érettségi, 2011. október, I. rész, 5. feladat
Témakör: *Függvények ( abszolútérték, paraméter) (Azonosító: mmk_201110_1r05f )

Az ábrán a valós számok halmazán értelmezett $f(x)= \left | x+a \right |+b$ függvény grafikonjának egy részlete látható. Adja meg a és b értékét!

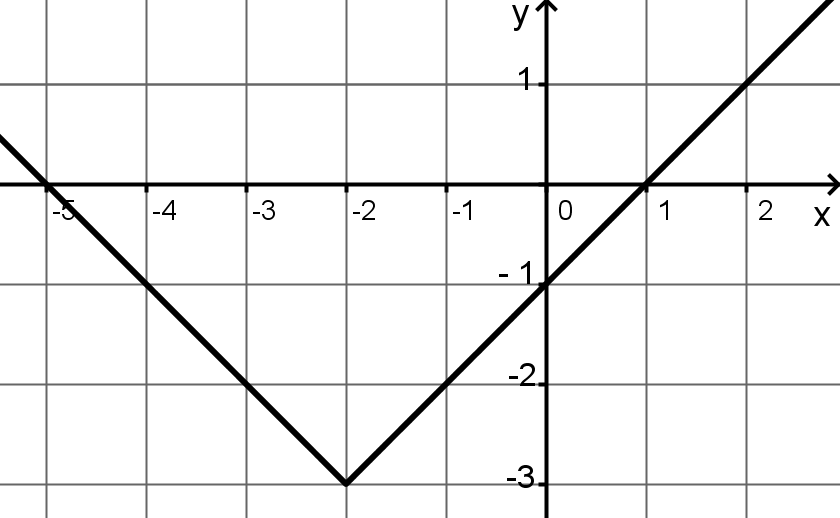
284. találat: Matematika középszintű érettségi, 2011. október, I. rész, 6. feladat
Témakör: *Statisztika (Azonosító: mmk_201110_1r06f )

Adja meg a 2; 11; 7; 3; 17; 5; 13 számok mediánját!

285. találat: Matematika középszintű érettségi, 2011. október, I. rész, 7. feladat
Témakör: *Kombinatorika ( gráfok) (Azonosító: mmk_201110_1r07f )

Rajzoljon le egy 4 pontú egyszerű gráfot, amelyben a pontok fokszáma rendre 3, 2, 2, 1!

286. találat: Matematika középszintű érettségi, 2011. október, I. rész, 8. feladat
Témakör: *Sorozatok (Azonosító: mmk_201110_1r08f )

Egy számtani sorozat ötvenedik tagja 29, az ötvenegyedik tagja 26. Számítsa ki a sorozat első tagját!

287. találat: Matematika középszintű érettségi, 2011. október, I. rész, 9. feladat
Témakör: *Algebra ( azonosság) (Azonosító: mmk_201110_1r09f )

Ha $a \neq 1$ , akkor az alábbi egyenletek közül melyik azonosság?

288. találat: Matematika középszintű érettségi, 2011. október, I. rész, 10. feladat
Témakör: *Függvények ( logaritmus) (Azonosító: mmk_201110_1r10f )

István az $x \mapsto \log_>x$ $x > 0$ függvény grafikonját akarta felvázolni, de ez nem sikerült neki, több hibát is elkövetett (a hibás vázlat látható a mellékelt ábrán).

Döntse el, hogy melyik igaz az alábbi állítások közül!

A) István rajzában hiba az, hogy a vázolt függvény szigorúan monoton csökkenő.

B) István rajzában hiba az, hogy a vázolt függvény 2-höz –2-t rendel.

C) István rajzában hiba az, hogy a vázolt függvény zérushelye 1.

289. találat: Matematika középszintű érettségi, 2011. október, I. rész, 11. feladat
Témakör: *Sorozatok ( mértani sorozat, logaritmus) (Azonosító: mmk_201110_1r11f )

A 2000 eurós tőke évi 6 %-os kamatos kamat mellett hány teljes év elteltével nőne 4024 euróra? Megoldását részletezze!

290. találat: Matematika középszintű érettségi, 2011. október, I. rész, 12. feladat
Témakör: *Térgeometria (Azonosító: mmk_201110_1r12f )

Az ábrán látható kockának berajzoltuk az egyik lapátlóját. Rajzoljon ebbe az ábrába egy olyan másik lapátlót, amelynek van közös végpontja a berajzolt lapátlóval! Hány fokos szöget zár be ez a két lapátló? Válaszát indokolja!

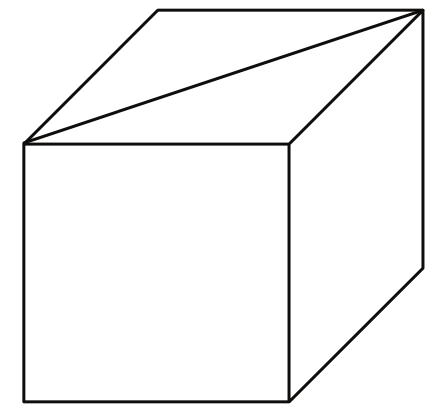
291. találat: Matematika középszintű érettségi, 2011. október, II. rész, 13. feladat
Témakör: *Algebra (gyökös egyenlet, trigonometrikus egyenlet, trigonometria) (Azonosító: mmk_201110_2r13f )

Oldja meg a valós számok halmazán az alábbi egyenleteket!

a) $ 5-x=\sqrt$

b) $\sin^2 x = 1+2 \cos x$

292. találat: Matematika középszintű érettségi, 2011. október, II. rész, 14. feladat
Témakör: *Statisztika (grafikon, valószínűségszámítás) (Azonosító: mmk_201110_2r14f )

Egy felmérés során két korcsoportban összesen 200 embert kérdeztek meg arról, hogy évente hány alkalommal járnak színházba. Közülük 120-an 40 évesnél fiatalabbak, 80 válaszadó pedig 40 éves vagy annál idősebb volt. Az eredményeket (százalékos megoszlásban) az alábbi diagram szemlélteti.

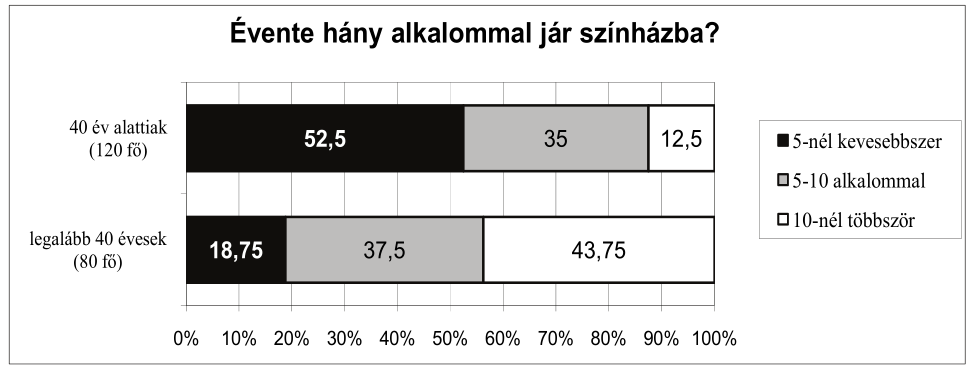
a) Hány legalább 40 éves ember adta azt a választ, hogy 5-nél kevesebbszer volt színházban?

b) A megkérdezettek hány százaléka jár évente legalább 5, de legfeljebb 10 alkalommal színházba?

c) A 200 ember közül véletlenszerűen kiválasztunk kettőt. Mekkora a valószínűsége annak, hogy közülük legfeljebb az egyik fiatalabb 40 évesnél? Válaszát három tizedesjegyre kerekítve adja meg!

293. találat: Matematika középszintű érettségi, 2011. október, II. rész, 15. feladat
Témakör: *Koordinátageometria (skalárszorzat, meredekség, hajlásszög) (Azonosító: mmk_201110_2r15f )

Adott két egyenes: $e: 5x-2y=-14,5$ ; $f: 2x+5y=14,5$ .

a) Határozza meg a két egyenes P metszéspontjának koordinátáit!

b) Igazolja, hogy az e és az f egyenesek egymásra merőlegesek!

c) Számítsa ki az e egyenes x tengellyel bezárt szögét!

294. találat: Matematika középszintű érettségi, 2011. október, II. rész, 16. feladat
Témakör: *Algebra (geometria, logaritmus) (Azonosító: mmk_201110_2r16f )

Újsághír: „Szeizmológusok számításai alapján a 2004. december 26-án Szumátra szigetének közelében kipattant földrengés a Richter-skála szerint 9,3-es erősségű volt; a rengést követő cunami (szökőár) halálos áldozatainak száma megközelítette a 300 ezret.”

A földrengés Richter-skála szerinti „erőssége” és a rengés középpontjában felszabaduló energia között fennálló összefüggés: $M=-4,42 + \dfrac \lg E$ .

Ebben a képletben E a földrengés középpontjában felszabaduló energia mérőszáma (joule-ban mérve), M pedig a földrengés erősségét megadó nem negatív szám a Richter- skálán.

a) A Nagasakira 1945-ben ledobott atombomba felrobbanásakor felszabaduló energia $ 1,344 \cdot 10^$ joule volt. A Richter-skála szerint mekkora erősségű az a földrengés, amelynek középpontjában ekkora energia szabadul fel?

b) A 2004. december 26-i szumátrai földrengésben mekkora volt a felszabadult energia?

c) A 2007-es chilei nagy földrengés erőssége a Richter-skála szerint 2-vel nagyobb volt, mint annak a kanadai földrengésnek az erőssége, amely ugyanebben az évben következett be. Hányszor akkora energia szabadult fel a chilei földrengésben, mint a kanadaiban?

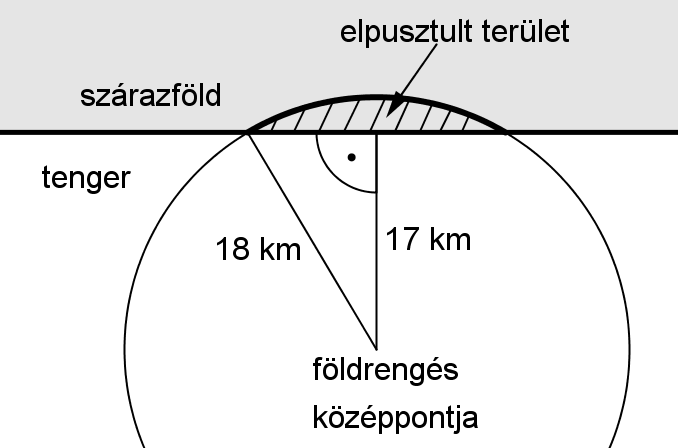
d) Az óceánban fekvő egyik szigeten a földrengést követően kialakuló szökőár egy körszelet alakú részt tarolt le. A körszeletet határoló körív középpontja a rengés középpontja, sugara pedig 18 km. A rengés középpontja a sziget partjától 17 km távolságban volt (lásd a felülnézeti ábrán). Mekkora a szárazföldön elpusztult rész területe egész négyzetkilométerre kerekítve?

295. találat: Matematika középszintű érettségi, 2011. október, II. rész, 17. feladat
Témakör: *Kombinatorika (számelmélet, oszthatóság) (Azonosító: mmk_201110_2r17f )

a) Hány olyan négy különböző számjegyből álló négyjegyű számot tudunk készíteni, amelynek mindegyik számjegye eleme az $\< 1; 2; 3; 4; 5; 6; 7\>$ halmaznak?

b) Hány 4-gyel osztható hétjegyű szám alkotható az 1, 2, 3, 4, 5 számjegyekből?

c) Hány olyan hatjegyű, hárommal osztható szám írható fel, amely csak az 1, 2, 3, 4, 5 számjegyeket tartalmazza, és e számjegyek mindegyike legalább egyszer előfordul benne?

296. találat: Matematika középszintű érettségi, 2011. október, II. rész, 18. feladat
Témakör: *Térgeometria (valószínűség, hasonlóság, binomiális eloszlás) (Azonosító: mmk_201110_2r18f )

Egy csonkakúp alakú tejfölös doboz méretei a következők: az alaplap átmérője 6 cm, a fedőlap átmérője 11 cm és az alkotója 8,5 cm.

a) Hány $cm^3$ tejföl kerül a dobozba, ha a gyárban a kisebbik körlapján álló dobozt magasságának 86%-áig töltik meg? Válaszát tíz $cm^3$ -re kerekítve adja meg!

b) A gyártás során a dobozok 3%-a megsérül, selejtes lesz. Az ellenőr a gyártott dobozok közül visszatevéssel 10 dobozt kiválaszt. Mennyi a valószínűsége annak, hogy a 10 doboz között lesz legalább egy selejtes? Válaszát két tizedesjegyre kerekítve adja meg!

297. találat: Matematika középszintű érettségi, 2012. május, I. rész, 1. feladat
Témakör: *Sorozatok (Azonosító: mmk_201205_1r01f )

Egy mértani sorozat első tagja 3, hányadosa (-2). Adja meg a sorozat első hat tagjának összegét!

298. találat: Matematika középszintű érettségi, 2012. május, I. rész, 2. feladat
Témakör: *Koordinátageometria (Azonosító: mmk_201205_1r02f )

Írja fel annak az e egyenesnek az egyenletét, amelyik párhuzamos a $ 2x-y=5$ egyenletű f egyenessel és áthalad a P(3; –2) ponton! Válaszát indokolja!

299. találat: Matematika középszintű érettségi, 2012. május, I. rész, 3. feladat
Témakör: *Függvények ( szélsőérték, másodfokú, parabola) (Azonosító: mmk_201205_1r03f )

Adott a valós számok halmazán értelmezett $f(x)=(x+2)^2+4$ függvény. Adja meg az f függvény minimumának helyét és értékét!

300. találat: Matematika középszintű érettségi, 2012. május, I. rész, 4. feladat
Témakör: *Logika ( kombinatorika, algebra) (Azonosító: mmk_201205_1r04f )

Döntse el, melyik állítás igaz, melyik hamis!

A) Hét tanulóból négyet ugyanannyiféleképpen lehet kiválasztani, mint hármat, ha a kiválasztás sorrendjétől mindkét esetben eltekintünk.