Matematika Gyakorlo Es Erettsegire Felkeszito Feladatgyujtemeny III Kek Small ocr

Részlet a 2022.-es melet szintű érettségi I. rész interktív videóból

MATEMATIKA GYAKORLÓ FELADATGYŰJTEMÉNY

1 MATEMATIKA GYAKORLÓ FELADATGYŰJTEMÉNY (Kezdő 9. évfolyam) A feladatokat a Borbás Lászlóné MATEMATIKA a nyelvi előkészítő évfolyamok számára című könyv alapján állítottuk össze.

2 I. Számok, műveletek számokkal. Töltsük ki a táblázat hiányzó részeit! a b c a+b-c -+- (-5)= a-(b+c) a-(b+c) (a+b)-c b-a+c a +b -ab. Végezd el a kijelölt műveleteket! a) + < [ (5 + ) ] + 96>+ = b) 9 < + [8 ( + ( )) + 5] 0>=. Gergő nyírja a füvet a kertben. A kert 7 m. Amikor lenyírta a terület részét, Domi 7 átvette tőle a fűnyírót. Hány m -t nyírt le Gergő? Mekkora rész maradt Dominak?. Anyu behozott a gyerekének egy tálca süteményt. A gyerekek megettek szelet süteményt. Ez az összesnek a 6 e volt. Hány szelet sütemény volt a tálcán? Egy gyerek az 7 összes süteménynek hányad részét ette meg, ha mindenki egyformán evett? 5. a) [ ] : [ ]= e) [ 7 8 ] [+ ] 0 = 9 b) : = f) 0 [+ ] : [+ 5 ] = c) [ ] 0 = g) [ ] : 7 [+ ] = d) 0 = h) 7: ( 9) =

3 6. Töltsük ki a táblázat hiányzó részeit! a b c ab + b: c , 0, 0, 0,75 0,5 0,5 (a + c): ( c) (ac bc): (b a): ( a) 7. Írd le növekvő sorrendben a következő számokat! a) – ; -; -,5; -0,0; – ; -5 b) -, ; ; -; 0; ; 0,5; -0; 5, 8 8. Töltsük ki a táblázat hiányzó részeit! a – 0 b a b a b a b (a b)(a + b) (a b) (a + b)

4 9. 5 csapból 5 óra alatt 0 m víz folyik ki. II. Egyenes arányosság, fordított arányosság a) Mennyi idő alatt folyik ki 0 csapból 0 m víz? b) Mennyi víz folyik ki a 0 csapból,5 óra alatt? c) Hány csapból folyik ki 5 m víz óra és 5 perc alatt? 0. 0 szüretelő 8 óra alatt 0 hordót töltött meg. a) Mennyi idő alatt tölt meg 60 szüretelő 0 hordót? b) Hány szüretelő tölt meg óra alatt 0 hordót? c) Hány hordót tölt meg 6 óra alatt 5 szüretelő?. Tavasszal, a Föld napja alkalmából az iskola tanulói az iskolához közeli erdőben egy közeli erdőben egy korábban megtisztított irtásterületen facsemetétek ültetnek. 0 gyerek 00 facsemetetét ültetett el egy nap. Ha mindenki ilyen munkatempóban dolgozik, akkor a) hány csemetét ültetnének el 5-en egy nap alatt? b) hány nap alatt ültettek volna el 0-en 50 csemetét? c) 00 facsemetét gyerek hány nap alatt ültetett volna el? d) 50 gyerek hány nap alatt ültetett volna el 50 csemetét?. Hány százaléka a) az 5-nek? d) a 8-nak? g) a 0-nak? j) 5 a -nek? b) a 0-nak? e) a 0-nek? h) az 50-nek? k) 5 a 0nek? c) a -nek? f) a 5-nek? i) a 5-nek? l) 5 a 0-nak?. Számítsd ki, hogy mennyi a) 5-nek a 80%-a, e) 60-nak az 50%-a, i) 680-nak a 0%-a b) 75-nek a 0/-a, f) 90-nek a 0%-a, j) 8-nak a 5%-a c) 0-nek a 60%-a, g) -nek az 5%-a, k) 0-nek a 5%-a d) -nak a 00%-a, h) 80-nek a 60%-a, l) 0-nak a 0%-a. A matematikatanár a dolgozatokat úgy osztályozza, hogy az eltérő maximális pontszám 85%-áért már jelest ad. Hány ponttól jeles a dolgozat, ha a maximális pontszám 0? 5. Egy vasúttársaságnál felmérést végeztek. Megnézték, hogy a Zamárdiba menő 8 órás vonaton hányan utaztak. 56 utast számoltak. Ez hány %-os kihasználtságot jelent, ha a vonaton 80 ülőhely volt? 6. Ágoston nagyon ügyesen pingpongozik. Az iskolai bajnokságon az eddig játszott mérkőzéseinek a 90%-át megnyerte. Hány mérkőzést játszott, ha most 6 pontja van? (A bajnokságban a nyert mérkőzésért pont, a vesztettért 0 pont jár, döntetlen nincs.) 7. A tej tömegének 7,%-a a tejszín, a tejszín 6%-a vaj. 500 kg tejből mennyi vaj lesz?

5 8. Ábrázold a következő függvényeket! III. Függvények a) f (x) = x + b) g(x) x c) h (x) = x + 9. Ábrázold az f (x) = x és a g (x) = x 9 függvényeket! a) Hol metszi a grafikon az az x tengelyt? b) Hol metszi a két grafikon egymást? c) Hol van az f függvény grafikonja a g függvény grafikonja fölött? 0. Néhány, a valós számokon értelmezett függvény grafikonját látod az ábrát: a) Melyik grafikon egyenes arányosság képe? b) Készítsd el a grafikon alapján az egyenes függvények értéktáblázatát 5 adatpárra! c) Melyik grafikon nem elsőfokú függvény képe? d) Állapítsd meg a hozzárendelési szabályokat! e) Melyik függvény növekvő, melyik csökkenő? f) Melyik függvény fejez ki egyenes arányosságot?. Ábrázold a valós számokon értelmezett f (x) = x függvényt! a) Milyen kapcsolatot látsz a x és a x függvény grafikonjai között? b) Hol növekvő, hol csökkenő a függvény? c) Van-e a függvénynek maximuma? Ha igen, hol? d) Van-e a függvénynek minimuma? Ha igen, hol? 5

6 e) Hol van a függvénynek zérushelye? Algebrai úton hogyan tudnád meghatározni? f) Határozd meg a függvény értékkészletét!. Ábrázold az f(x) = (x ) függvényt a [ ; ] intervallumon! Válaszolj az alábbi kérdésekre! a) Hol növekvő a függvény? b) Hol csökkenő a függvény? c) Van-e a függvénynek maximuma? Ha igen, hol? d) Van-e a függvénynek minimuma? Ha igen, hol? e) Hol van a függvénynek zérushelye? Algebrai úton hogyan tudnád meghatározni? f) Határozd meg a függvény értékkészletét!. Az ábrán néhány másodfokú függvény képletét láthatod. Olvass le néhány összetartozó értékpárt, s állapítsd meg a hozzárendelési szabályt!. Ábrázold a következő valós számokon értelmezett függvényeket a kifejezés melletti intervallumon! a(x) = (x ) [ ; ] d(x) = (x + ) + [ ; ] b(x) = x [ ; ] e(x) = (x + ) [ ; ] c(x) = (x ) + [ ; ] 6

7 5. Ábrázold az f(x) = x + függvényt a [ 5; ] intervallumon! Válaszolj az alábbi kérdésekre! a) Milyen kapcsolatot látsz a x + és x + függvény grafikonjai között? b) Hol növekvő, hol csökkenő a függvény? c) Van-e a függvénynek maximuma? Ha igen, hol? d) Van-e a függvénynek minimuma? Ha igen, hol? e) Hol van a függvénynek zérushelye? Algebrai úton hogyan tudnád meghatározni? f) Határozd meg a függvény értékkészletét! 6. Ábrázold a valós számokon értelmezett következő függvényeket a kifejezés melletti intervallumon! Majd válaszolj az előző feladatban föltett kérésekre! a(x) = x [ ; ] b(x) = x [ ; ] c(x) = x + [ ; ] d(x) = x + + [ ; ] e(x) = x + [ ; ] 7. Az ábrán néhány abszolútérték-függvény képét látod. Olvass le néhány összetartozó értékpárt, s állapítsd meg a hozzárendelési szabályt! 7

8 IV. Műveletek algebrai kifejezések 8. Az áruházban egy kazetta ára m Ft. Egy másik típusú kazetta 70 Ft-tal kerül többe. Egy video ára 70-szerese az olcsón kazettának. Menyibe kerül a drágább kazetta, és mennyibe kerül a video? 9. Mennyi az 5 a-szorosánál -vel több? Mennyi ez a szám, ha a=. 5, 6, 7, 8, 0,? 0. Írd fel az a, b, c betűk segítségével az alábbi műveleteket! a) Két szám (a és b) összegének a -szerese! b) Két szám (a és b) különbségének a háromszorosa! c) Két szám (a és b) különbségének az egyharmada! d) Az (a és b) szorzatának és a (b és c) szorzatának az összege! e) Két szám (a és b) összegének és ugyanennek a két számnak a különbségének a szorzata! f) Két szám (a és b) különbségének és ugyanennek a két szám különbségének a szorzata! g) A táblázat adatainak alapján számítsd ki a feladat kifejezéseinek a helyettesítési értékét!. Válaszd ki az egynemű kifejezéseket, és add össze azokat! a) a b d) 5xy z g) x y j) xzy b) x y e) x y h) a b k) b a c) ab f) 5a b i) 5ab l) zyx. Vond össze az egynemű tagokat! a) 5a b + a b 9a b c) x + x + x 8x b) p q + q p d) 5ab a b 7a b a b + 5ab 8a b. Vond össze az egynemű tagokat! a) k – m – 5 k + m b) 5 x y xy – 5 x y+ 5 x y c) a b + ab a b + ab d) 5 (x + y) (x + y) 5 (x + y) e) (x y ) + 5(x y ) (x y ) + 7(x y ) 8

9 . Végezd el a kijelölt műveleteket! a) (6a + ) (a 5) b) 6a + a 5 c) (6a + ) a 5 d) 6a + (a 5) 5. Végezd el a kivonásokat, ahol lehet, vonj össze! a) x (x + y) b) x (x y) c) 5a (b + a) d) (u + 5v) (5u + v) e) (5b + 6b) (5b + 6b ) f) (0x + y) (0y + x) g) (00x + 0y + z) (00z + 0y + x) h) (7a ab b) (a ab + b ) i) (uvz vzw + zwx) ( uvz + zxw) 9

10 V. Egyenletek, egyenlőtlenségek 6. Oldd meg a következő egyenleteket az egész számok halmazán! a) x 7 + 8x = 9x x b) x + x = 00 9x c) x 0 + 6x = 8x 0 + x d) 0x x = x x e) x x = x x f) x + x + 9 = x x 7 5 x + 5 g) +,5x +,6 = x ,x h) 0,75x x = 9 + 0,6x 0,5x 7. Oldd meg az alábbi egyenleteket a racionális számok halmazán! a) x 8(x ) = 7x 5( x) b) 7(x ) 6( x) = (x + ) c) (x + ) = 8( x) 5(x ) d) 7( x) 5(x + ) = 8( 7x) 8. Oldd meg az alábbi egyenleteket a racionális számok halmazán! a) b) c) x + x x = 7 x 5 + x 7 x 5 = x + x 6 x 9 = d) x + x x = 9. Oldd meg az alábbi egyenleteket a racionális számok halmazán! a) b) y+ x+7 5 = 5y 7 x 7 c) x + = x+ d) x + x 7 = x+ 5 x 8 = 5 x+6 0. Egy alkalommal Zsolti és Dóri összesen 600 Ft-ot kapott. Zsolti pénzének 5%-a annyi, mint Dóri pénzének a 5%-a. Mennyi pénzt kapott Zsolti, mennyit Dóri?. István édesapja éves volt, amikor István született. Most négyszer annyi idős, mint István. Hány éves István, hány éves az édesapja? 0

11 . Feles Elek és Stüszi Vadász szomszédok. Kertjeik összterülete 759 m. A területek aránya pedig 5:6. Mekkora kertje van Feles Eleknek és Stüszi Vadásznak külön-külön, ha tudjuk, hogy Stüszi Vadász kertje a kisebb?. Kétféle cukorkából 8 kg keveréket készített Mariska néni. Az egyik cukorka ára kg-onként 0 Ft, a másiké 00 Ft. A keveréket 50 Ft-ért árulta Mariska néni. Mennyi cukorkát használt Mariska néni az egyes fajtákból?. Oldd meg az alábbi egyenlőtlenségeket a pozitív egész számok halmazán! Szemléltesd a megoldást számegyenesen! a) 8(x + ) > 8 c) (y 5) b) (x + ) < 60 d) 5(x ) (x ) 5. Oldd meg az egyenlőtlenségeket a negatív számok halmazán! Szemléltesd a megoldást számegyenesen! a) 7(x ) 6( x) >(x + ) b) (x + ) 8( x) 5(x ) c) y ( 0 y) 6y 7( y) d) 7( x) 5(x + ) 8( 7x)

12 VI. Geometria 7. Határozd meg az a alapú egyenlőszárú háromszög keresett adatait, számítsd ki a háromszög kerületét és területet! a) a = cm b = 0 cm m a =? b) a = 0 cm b =? m a = 8 cm c) a =? b =,5 cm m a = 0,8 cm 7. Egy egyenlőszárú háromszög átfogója 5cm. Mekkora a befogója? 8. Milyen távol van a cm sugarú kör középpontjától egy 5cm hosszú húr? 9. Egy szabályos háromszög kerülete 9, cm. Mekkora a területe? 50. Egy téglalap aránya :, az átlója,0 dm. Mekkora a kerülete? 5. Egy négyzet átlója cm. Mekkora az oldala? 5. Egy szabályos háromszög 7 cm. Mekkora az oldala? 5. Egy egyenlő szárú trapéz alapjai 0 cm és 7 cm. A szárai 5 cm hosszúak. Mekkora a trapéz területe? 5. Egy rombusz átlói 8 cm és 6 cm hosszúak. Mekkora a rombusz kerülete és területe? 55. Egy háromszög két belső szögének nagysága a) 0 és 60 b) 5 és 75 Határozzuk meg a háromszög harmadik belső szögét és külső szögeit. 56. Jelölje α, β, γ egy háromszögbelső szögeit, és legyenek α, β, γ a megfelelő külső szögek. A következő adatok alapján határozzuk meg a háromszög hiányzó és külső szögeit. a) α= 5, β = 80 b) α=56 β = 57. Egy háromszög belső szögeinek aránya a) :: b) :5:6 Határozzuk meg a háromszög belső és külső szögeit. 58. Egy háromszög belső szöge 8. A másik két belső szög közül az egyik -kal nagyobb a másiknál. Mekkorák a háromszög belső és külső szögei? 59. Egy konvex négyszög belső szögei α, β, γ, δ, a megfelelő külső szögek rendre α,β,γ,δ. Számítsuk ki a megfelelő belső és külső szögeket, ha a) α = 00, β = 7, γ = 8. b) α = 70, β = 5, γ = Mekkorák a trapéz belső és külső szögei, ha két szemközti belső szöge? a) 60 és 0 b) 5 és 00

13 6. Számítsuk ki a paralelogramma belső és külső szögeit, ha egyik belső szöge a) 0. b) Számítsuk ki a deltoid belső szögeit, ha két szomszédos belső szöge a) és 8. c) 0 és 8.

14 Megoldások I. Számok, műveletek számokkal:. a b c a+b-c -+- (-5)= a-(b+c) a-(b+c) (a+b)-c b-a+c a +b -ab a) 0; b) 0.. m ; 5 7 rész.. szelet; 7 rész. 5. a) 7 6 b) c) 7 d) 97 e) 0 f) 8 9 g) 6 h) 6. a b c , 0, 0, 0,75 0,5 0,5 ab + b: c ,9,8 (a + c): ( c) ,6,8 (ac bc): (b a): ( a)

15 7. a) 5; ;,5; ; ; 0,0 b) 0;,; ; 0; 0,5; ;, 5, 8 8. a – 0 b a b a b a b (a b)(a + b) (a b) (a + b) II. Egyenes arányosság, fordított arányosság 9. a) 5 óra; b) 0 m ; c) 5 csapból. 0. a) 8 óra; b) 0 szüretelő;c) 0 hordó.. a) 50 csemete; b),5 nap; c) 5 nap; d) fél nap.. a) 80%; b) 5%; c) 50%; d) 7,5%; e) 0%; f) 6%; h) 6%; i) %; j) 50%; k) 50%; l) 50%. a) ; b) 5; c) ; d) 9; e) 80; f)78; g),; h) 50; i) 7; j) 5; k),5; ) 0. 5,5 ponttól % 6. 0 mérkőzés. 7.,6 kg. 5

16 III. Függvények

17 0. a) h, g; b) pl. j(x) x – – 0,5 j(x) 0,5,5,75 c) k; d) f (x) = -x; h (x) = x; j(x) = 0,5x+; k(x) = 6,5; e) f és g csökkenő, h és j növekvő, k állandó f) g és h egyenes arányosság. f) Melyik függvény fejez ki egyenes arányosságot?. a) b) A két függvény grafikonja egymás tükörképei az x tengelyre vonatkozóan. c) csökkenő:x > 0, növekvő: x < 0 d) maximum: x = 0-nál az y = 0 e) minimum nincs f) zérushely: x = 0; algebrai úton a x = 0 egyenlet megoldásával g) értékkészlet: y 0 7

18 . a) növekvő: [; ] b) csökkenő: [ ; ], c) maximum: x = nél y = 9 d) minimum: x = nél y = 0 e) zérushely: x = 0; algebrai úton a (x + ) = 0 egyenlet megoldásával f) értékkészlet: [0; 9]. f (x) = (x 5) ; g (x ) = x + 9; h (x) = (x + ) 9 8

19 . 5. a) A két függvény grafikonja egymás tükörképei az x tengelyre vonatkozóan. b) csökkenő: x >, növekvő: x < c) maximum: x = -nál az y = 0 d) minimum: x = -nél az y = 9

20 e) zérushely: x = ; algebrai úton a x + = 0 egyenlet megoldásával f) értékkészlet: y 0 6. a(x): ha x, csökkenő, ha x, növekvő nincs maximum; x = -nél minimum, zérushely: x = ; értékkészlet: a(x) 0; b (x): ha x 0; csökkenő; ha x 0; növekvő; nincs maximum; x = 0-nál minimum; zérushely: x = és x = ; értékkészlet: b (x) ; c (x) : ha x, csökkenő, ha x, növekvő nincs maximum; x = -nél minimum; zérushely: nincs; értékkészlet : c (x) ; d (x): ha x, növekvő ha x, csökkenő; maximum x = -nél; nincs minimum zérushely: x = és ; értékkészlet d (x) ; e(x:) ha x, növekvő ha x, csökkenő; nincs minimum; x = -nél maximum; zérushely: nincs; értékkészlet: e (x). 7. f(x) = x + 9 g(x) = x 5 h(x) = x + 9 0

21 IV. Műveletek algebrai kifejezésekkel 8. kazetta m + 70 Ft, videó 70m Ft 9. 5a + ; 7; ; 7; ; 7; ; 5; 6, 0. a) ( a + b); b) ( a b); c) (b a); d) ab + bc; e) (a + b) ( a b) f) (a b) (a b). a), h), összeg 0; b), e), összeg x y; c), i) összeg 8a b ; d) j összeg 7xy z; f), k), összeg 8 a b ; g), l, összeg x yz. a) 0 5 b) 6 6 c) d) – 0 e) f) ,8-0, 0 0,5-0,09 0,0. a) 9a b 9a b; b) b q ; c) 7x + 5x; d) 0ab a b a b. a) 7 0 k 7 m ; b) 5 x y xy ; c) a b + ab ; d) 0 (x + y) ; e) (x y ).. a) x y b) y c) -b; d) v u ; e) b b f) 9x 9y; g) 99x 99z; h) 5a ab b i i) uvz uvw + zwx. 5. a) a a 5; b) a 5; c) a + 6a 5; d) a 5. V. Egyenletek, egyenlőtlenségek 6. a) ; b) ; c) -; d) ; e)5; f) -; g) ; h) nem egész: 6 7. a) ; b) 5; c) d) nincs megoldása a) ; b) 5; c) 9 d) 8 9. a) 6 ; b) ; c) 6 ; d) Zsolti 50-Ft-ot, Dóri 50 Ft-ot.. István éves., édesapja 56.. Stüszi Vadásznak 5 m, Feles Eleknek m.. 5 kg a 0 Ft-osból és kg a 00 Ft-osból.

23 α = 7, β = 5, γ = 7, ρ = 5 6. a) α = 78, β =, γ = 8, ρ = vagy α =, β = 8, γ = 6, ρ = 8 c) α = 0, β = 8, γ = 0, ρ = 8

Matematika Gyakorlo Es Erettsegire Felkeszito Feladatgyujtemeny III Kek Small ocr

We believe everything in the internet must be free. So this tool was designed for free download documents from the internet.

Legal Notice

We are not associated with any website in anyway.

Disclaimer

Designed and built with ♥ by Erik Fong. Licensed under the MIT License. The source code can be found at Github.

♥ Please donate to keep our website running. ♥

BITCOIN: 1JBEG65wHHw1TpjJps52vMR5vYZhggQmNG
ETHEREUM: 0x4B6F4c9817eec0BFa7e1c51B232a114de0Bc9B2B

MATEMATIKA MEGOLDÁSOK I. EGYSÉGES ÉRETTSÉGI FGY

Az új, kétszintű érettségi vizsga előkészítése keretében, a középszintű matematikavizsgára való felkészülést szolgáló feladatgyűjtemény megoldáskötetét tartja kezében az olvasó. Tekintettel arra a tartalmi megújulásra, melyet a nemzeti alaptanterv,a kerettanterv, az érettségi vizsgakövetelmények előirnak, és amely tükröződik a feladatgyűjtemény összeállításán, valamennyi feladat megoldását elkészítettük. Ennek eredményeként három kötetet töltenek meg a megoldások.

Emelt szintű matematika érettségi 2022 feladatok: ezek voltak a feladatok a megoldásokkal együtt!

Dancsó Imre, 2022. augusztus 19.

A 2022-es emelt szintű érettségi nem okozott különösebb meglepetéseket. A szokásos témakörök jelentek meg, többnyire olyan arányban, ahogy azt megszokhattuk.

A feladatsor első fele (az első négy feladat), ami mindenki számára kötelező változatos, egymástól eltérő témákat hozott. Diákbarátnak mondható feladatok voltak, de azért megjelent egy-két nehezebb részfeladat is. A második részben, ahol 5 feladat közül 4-et kell megoldani már igen sokszínűek voltak a példák. Előfordult, hogy egy feladaton belül (6.) mind a három részfeladat külön témakörrel foglalkozott. A feladatsor nem volt könnyű, sokat kellett számolni benne és profin tudni az összefüggéseket, de nagy varázslatot nem igényeltek a példák. de úgy gondoljuk mindenki ki tudta választani azt az egy példát, ami számára barátságtalan.

Emelt szintű matematika érettségi 2022: milyen feladatok voltak?

Itt egy gyors összefoglaló, hogy melyik témakörből mennyi pontot lehetett szerezni az érettségin. Meglepetésnek számít, hogy az előző évi májusi feladatsorhoz képest mekkora az eltérés.

1. helyezett: Egyenletek és algebra 25 pont
2. helyezett: Függvények és analízis 15 pont
3. helyezett: Valószínűségszámítás 15 pont
4. helyezett: Sorozatok és Síkgeometria 13-13 pont
5. helyezett: Kombinatorika és Koordinátageometria 11-11 pont
6. helyezett: Térgeometria 8 pont
7. helyezett: Gráfok 7 pont
8. helyezett: Százalékszámítás és Statisztika 5-5 pont

Nézzük részletesen a feladatokat – megoldásokkal együtt!

Itt megtalálod a 2022-es emelt szintű matematika érettségi 1-3. feladatait interaktív megoldásokkal, amikből nagyon sokat tanulhatsz:

Részlet a 2022.-es melet szintű érettségi I. rész interktív videóból

Hasonló interaktív videókon átnézhetsz minden matek érettségi témakört, és begyakorolhatod az érettségi feladatok megoldását.

Ezek voltak a feladatok (I. rész):

1. Oldja meg a valós számok halmazán az alábbi egyenleteket!

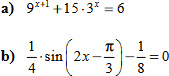
2.
a) Egy számtani sorozat első tagja 5, differenciája 3, az első n tag összege pedig 4900. Határozza meg n értékét! (5 pont)

b) Egy mértani sorozat első és második tagjának összege 6, harmadik és negyedik tagjának összege pedig 96. Adja meg a sorozat első tagját és hányadosát! (8 pont)

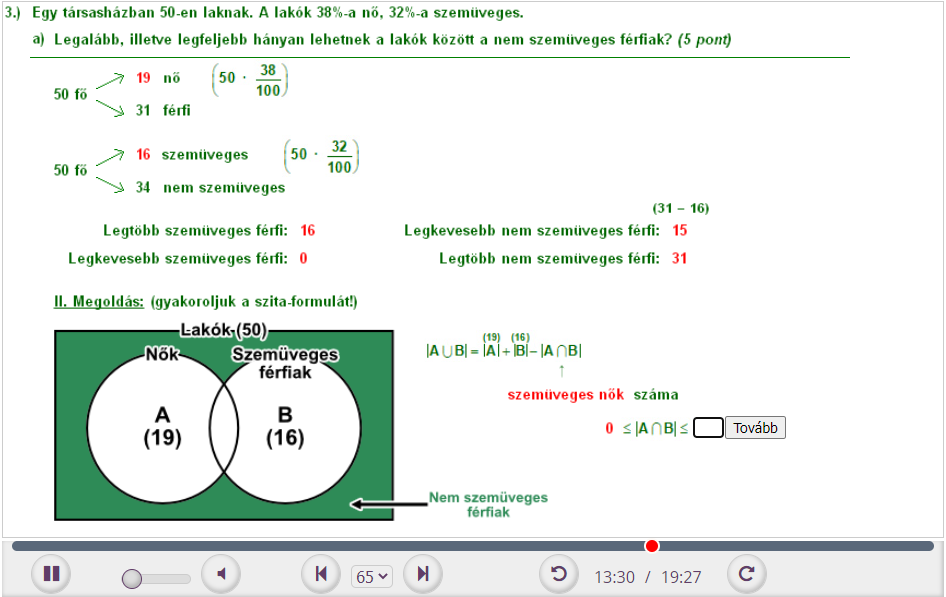
3.) Egy társasházban 50-en laknak. A lakók 38%-a nő, 32%-a szemüveges.

a) Legalább, illetve legfeljebb hányan lehetnek a lakók között a nem szemüveges férfiak? (5 pont)

A társasház kertje egy 15 méter hosszú, 10 méter széles téglalap alakú földterület, amely az egyik átlója mentén ketté van osztva: az egyik fele füvesítve van,
a másik felén virágágyás található. A füvesített rész derékszögű csúcsában van egy öntöző, amely egy 10 méter sugarú negyedkör alakú területet locsol a kertben.

b) Mekkora az a füvesített terület, amelyet nem ér el az öntöző? (8 pont)

4. Egy biliárdgolyó készletben található 9 golyó tömegére a következő mérési eredményeket kapták (grammban): 163, 163, 163, 163, 163, 164, 165, 166, 166.
Egy ilyen készletet akkor hitelesítenek a minőségellenőrzésen, ha az alábbi feltételek mindegyikének megfelel:

• minden golyó tömege legalább 160 gramm és legfeljebb 170 gramm;
• a golyók tömegének terjedelme legfeljebb 3 gramm;
• a golyók tömegének szórása legfeljebb 1 gramm.

a) Hitelesíthető-e ez a készlet? (5 pont)

Egy dobozban 3 piros és 7 kék golyó található.

b) Kihúzunk a dobozból egymás után két golyót úgy, hogy az elsőként kihúzott golyót a húzás után nem tesszük vissza. Határozza meg annak a valószínűségét,
hogy a kihúzott két golyó között lesz piros! (4 pont)

c) Kihúzunk a 10 golyó közül egymás után három golyót úgy, hogy a kihúzott golyót a következő húzás előtt mindig visszatesszük. Legyen az A esemény az,
hogy a kihúzott három golyó közül pontosan kettő piros, a B esemény pedig az, hogy a kihúzott golyók között van piros.
Határozza meg a P(A | B) valószínűséget! (5 pont)

A 2022. emelt szintű érettségi feladatok II. része:

5. Lali, Pali és Vali egy palacsintázóban ebédelnek. Lali 3 mogyorókrémes, 1 túrós és 2 fahéjas palacsintáért 1500 Ft-ot, Pali 4 mogyorókrémes, 2 túrós és 1 fahéjas palacsintáért
1740 Ft-ot, Vali pedig 1 mogyorókrémes, 2 túrós és 2 fahéjas palacsintáért 1170 Ft-ot fizetett.

a) Mennyibe kerül 1-1 darab a különböző fajta palacsintákból? (8 pont)

Lali vesz még egy lekváros palacsintát 210 Ft-ért. Lali zsebében 100, 50, 20, 10 és 5 Ft-os érmék vannak, mindegyikből több is. Ezek közül 6 érmét választ ki.

b) Igazolja, hogy 6 érmével három különböző módon fizethető ki 210 Ft! (Két fizetést különbözőnek tekintünk, ha legalább az egyik címletű érméből eltérő számút
használunk fel a két fizetés során.) (5 pont)

c) Hányféle sorrendben vehet elő Lali 6 olyan érmét a zsebéből, amelyek összege 210 Ft, ha egyesével húzza elő őket? (Az azonos címletű érméket nem
különböztetjük meg egymástól.) (3 pont)

6. Egy egyenlőszárú háromszög csúcsai a derékszögű koordináta-rendszerben A(0 ; 0), B(82 ; 0) és C(41 ; 71). Géza szerint ez a háromszög szabályos.

a) Határozza meg a háromszög szögeit fokban, három tizedesjegyre kerekítve! (5 pont)

b) Határozza meg a háromszög AC és AB oldalainak arányát négy tizedesjegyre kerekítve! (3 pont)

Egy csonkakúp alapkörének sugara 14 cm, fedőkörének sugara 8 cm, alkotója 10 cm hosszú. Géza szeretné gyorsan megbecsülni a csonkakúp térfogatát,
ezért azt egy henger térfogatával közelíti. A közelítő henger alapkörének sugara megegyezik a csonkakúp alap- és fedőköre sugarának számtani közepével,
magassága pedig egyenlő a csonkakúp magasságával.

c) Határozza meg Géza közelítésének relatív hibáját! (Relatív hibának nevezzük a közelítő értéknek a pontos értéktől mért százalékos eltérését.) (8 pont)

7. Flóra kétfajta lisztből süt kenyeret. A kenyérhez a recept alapján 5 : 4 arányban kell búzaliszt és rozsliszt. Eredetileg 450 gramm búzalisztet és 400 gramm rozslisztet
kevert össze, de további, összesen 500 gramm liszt hozzáadásával sikerült elérnie a recept által előírt arányt.

a) A hozzáadott 500 gramm lisztből hány gramm volt a búzaliszt? (3 pont)

Ha egy cég x tonna lisztet állít elő egy nap alatt (0 2 (x − 3)(1,5 − x) képlet adja meg, a nyereségét képlet adja meg, a nyereséget tízezer tallérban számítva. (Negatív helyettesítési érték
veszteséget jelent.)

b) Mutassa meg, hogy csak 1,5 2 + 2y = 16 egyenletű parabola é az x 2 + (y − 3) 2 = 9 egyenletű kör.

a) Határozza meg a parabola fókuszpontjának és a kör középpontjának a koordinátáit! (4 pont)

b) Igazolja, hogy a Q(2√ 2 ;4) pont a par abolának és a körnek is pontja, és a kör Q-ban húzott érintője érinti a parabolát is! (7 pont)

c) Határozza meg a parabola és az x tengely által közrezárt korlátos síkidom területét! (5 pont)

A feladatokat és a megoldókulcsot innen letöltheted:

Ha sok hiányosságod van még, az intenzív tréninggel bepótolhatod, és egy klassz érettségit írhatsz!

Hihetetlenül gyorsan tudsz fejlődni matekból az egyedi módszereknek és a jól felépített tananyagnak köszönhetően.

A törtek összeadása és kivonása egyszerűen

Hogyan kell a törteket összeadni? Hogyan kell a vegyes törteteket összeadni egymással, kivonni egymásból?