Emelt matematika 11. osztály
A Matekból Ötös 11. osztályosoknak: • csak gyermekedre figyel, hiszen egy oktatószoftver gyermeked laptopján; • türelmes, mert annyiszor oldja meg a feladatokat és nézheti meg az elméletet ahányszor csak akarja; • érthetően magyaráz, mert a teljes 11.-es matematikaanyagot közérthető és barátságos formába öntöttük – ez a matek végre nem harap;
Matematika 11. – Az érthető matematika – NT-16312
Az érthető matematika tankönyvsorozatban – az alkotók szándéka szerint – a matematikai ismeretek könnyen megérthetők és a bonyolultnak tűnő problémák is megoldhatók. A tankönyv elsősorban a középszintű érettségi tananyagát tartalmazza, de kiegészítő anyagként megtalálható benne mindaz, ami a 11. évfolyamon megérthető és az emelt szintű érettségi vizsgán kérdezhető. Lehetővé téve ezzel azt, hogy már a középiskola első évétől kezdve mindenki folyamatosan tudjon felkészülni az érettségire, akár középszinten, akár emelt szinten szeretne majd vizsgázni. Fokozatosan nehezedő, jól kidolgozott példák vezetik be a tanulókat az elsajátítandó tananyagba. A gyakorlást, az otthoni tanulást és az érettségire vizsgára való felkészülést a leckék végén található feladatok segítik. A feladatok részletes megoldása megtalálható a kiadó honlapján. Az érdeklődő vagy otthon gyakorolni vágyók számára még további feladatokat is ajánlunk, amelyeket a Nemzeti Tankönyvkiadó Matematika Gyakorló és érettségire felkészítő feladatgyűjtemény családjából jelöltünk ki.
Emelt matematika 11. osztály

Próbáld ki, mennyire világos és érthető velünk a matek! Megmutatjuk, hogyan működik nálunk a matek felkészítés. Garantáljuk, hogy velünk megérted és még emlékezni is fogsz rá. Ezt szeretnénk itt bemutatni.

A hiányosságok pótlása
- Útmutató
Ha vannak elmaradásaid az előző évekből, azokat gyorsabban és könnyebben pótolhatod, mint gondolnád! A “Pótold a hiányosságaidat” modul segít, ha szeretnél jobb eredményeket matekból.

5 lépéses Matek Oázis-módszer
- Útmutató
Megmutatjuk, miért különleges, és mitől működik olyan jól az 5 lépéses Matek Oázis módszer. Tutti, hogy velünk megérted a matekot, és valódi, alkalmazható tudásra tehetsz szert.

Hogyan használd a Matek Oázist?
- Útmutató
Hogyan érdemes használni a matek videókat, hogy a legjobb eredményt érjétek el matekból szórakoztató módon tanulva? Velünk nem csak a matekot gyakorolhatod, hanem csillagokat, érmeket, kupákat is gyűjthetsz. Lépésről lépésre elmondjuk, hogyan kezdj hozzá, és hogyan folytasd. Célunk, hogy mindent érts, és a feladatokat is meg tudd oldani. Akár 4-szer gyorsabban haladhatsz, mint a suliban, mivel interaktívan, az alapoktól kezdve és szemléltetve magyarázunk.
A hét legnépszerűbb videója (hétfőnként cseréljük)

Szinusz- és koszinusz-tétel
-
Tananyag
Ez a matematikai oktatóvideó a szinusz és koszinusz-tétel használatára tanít meg téged. Fontosak ezek a tételek, hisz minden háromszögben alkalmazhatók. Ha a háromszög oldalai és szögei közül hiányzó adatokat kell kiszámolnunk, bizonyos esetekben a szinusztételt, máskor a koszinusz-tételt kell használni. Azt is megtanulhatod a videóról, mikor melyik tételt kell használni. Kattints és nézz körül az évfolyam videói között!
HOL IS KEZDJEM?
2 alfejezet / 5 tananyag
01. HOGYAN HASZNÁLD?
- Neked is lehetnek jobb eredményeid matekból!
Próbáld ki, mennyire világos és érthető velünk a matek! Megmutatjuk, hogyan működik nálunk a matek felkészítés. Garantáljuk, hogy velünk megérted és még emlékezni is fogsz rá. Ezt szeretnénk itt bemutatni.
Ha vannak elmaradásaid az előző évekből, azokat gyorsabban és könnyebben pótolhatod, mint gondolnád! A “Pótold a hiányosságaidat” modul segít, ha szeretnél jobb eredményeket matekból.
Megmutatjuk, miért különleges, és mitől működik olyan jól az 5 lépéses Matek Oázis módszer. Tutti, hogy velünk megérted a matekot, és valódi, alkalmazható tudásra tehetsz szert.
Hogyan érdemes használni a matek videókat, hogy a legjobb eredményt érjétek el matekból szórakoztató módon tanulva? Velünk nem csak a matekot gyakorolhatod, hanem csillagokat, érmeket, kupákat is gyűjthetsz. Lépésről lépésre elmondjuk, hogyan kezdj hozzá, és hogyan folytasd. Célunk, hogy mindent érts, és a feladatokat is meg tudd oldani. Akár 4-szer gyorsabban haladhatsz, mint a suliban, mivel interaktívan, az alapoktól kezdve és szemléltetve magyarázunk.
02. A hét legnépszerűbb videója (hétfőnként cseréljük)
- Szinusz- és koszinusz-tétel
Ez a matematikai oktatóvideó a szinusz és koszinusz-tétel használatára tanít meg téged. Fontosak ezek a tételek, hisz minden háromszögben alkalmazhatók. Ha a háromszög oldalai és szögei közül hiányzó adatokat kell kiszámolnunk, bizonyos esetekben a szinusztételt, máskor a koszinusz-tételt kell használni. Azt is megtanulhatod a videóról, mikor melyik tételt kell használni. Kattints és nézz körül az évfolyam videói között!
Trigonometria
Hegyesszögek szögfüggvényei
Csillagaim: 0 /18

Szögfüggvények derékszögű háromszögekben
-
Tananyag
A szögfüggvények ismerete nagyon fontos a geometriai számításokban. Derékszögű háromszögek hiányzó adatait a szinusz (sin), koszinusz (cos), tangens (tg), kotangens (ctg) szögfüggvények segítségével könnyedén kiszámíthatjuk. Nézd át mindezt ezen az interaktív oktatóvideón, és gyakorold velünk a sin, cos, tg, ctg szögfüggvények használatát!

Hegyesszögek szögfüggvényei
-
Játék
JÁTÉK! Telepítsd be a tengeri akváriumot! Derékszögű háromszögekben keressük az alfa vagy a béta szög szögfüggvényeit. El kell döntened, hogy a felírt tört a megadott szög szinuszával, koszinuszával, vagy épp tangensével-kotangensével egyezik meg. Látni fogod utána a magyarázatot is, így a végére már magabiztosan fogod tudni használni a szögfüggvényeket.

Szögfüggvények derékszögű háromszögekben
-
Teszt
TESZT! Hét feladat megoldásával gyakorolhatod a szögfüggvények használatát derékszögű háromszögekben. Oldd meg a feladatokat önállóan! Kiértékelés után levezetjük a megoldást lépésről lépésre.

Szögfüggvények alkalmazása
-
Tananyag
Ez a videó a szögfüggvények alkalmazásával foglalkozik. Sorra vesszük a nevezetes (30, 45, 60 fokos) szögek szögfüggvényeit. Alkalmazzuk a szögfüggvényeket sík-és térgeometriai feladatokban.

Szögfüggvények és alkalmazásuk
-
Teszt
TESZT! Feladatok segítségével tedd próbára tudásod, mennyire sikerült elsajátítanod a szögfüggvényekről tanultakat. Oldd meg a feladatokat önállóan! Kiértékelés után levezetjük a megoldást lépésről lépésre.

TESZT! Hegyesszögek szögfüggvényei
-
Teszt
TESZT! Keresd a derékszögű háromszögeket, és a szögfüggvények segítségével határozd meg a hiányzó oldalakat, szögeket! Dolgozz önállóan, majd ellenőrizd a magad! Kiértékelés után láthatod a részletes megoldásokat!
Szögfüggvények általánosítása
Csillagaim: 0 /15

A sin x általánosítása
-
Tananyag
Ebben a matek tananyagban a szinusz szögfüggvény általánosítását vezetjük be, megnézzük a függvény tulajdonságait és a szinuszos alapegyenleteket. Azt is részletesen elmagyarázzuk, mi is az a radián, mert erre is szükség van a trigonometrikus egyenletek megoldásához.

A cos x általánosítása
-
Tananyag
Ebben a matek tananyagban a szinusz-függvény után a koszinusz-függvény általános definícióját, a koszinusz-függvény tulajdonságait és az ezek ismeretében megoldható egyszerű trigonometrikus egyenletek megoldását nézzük át. Feladatokkal gyakorlunk.

A tg x és ctg x általánosítása
-
Tananyag
A tg x és ctg x alkalmazását és függvényeiket vizsgáljuk ebben a videóban. Meghatározzuk a definíciót: tg x = a megoldása; ctg x = a megoldása. Megvizsgáljuk koordináta-rendszerben is, vajon növekszik vagy csökken-e a függvény. Hol lehet értelmezni a függvényt?

Gyakorlás – szögfüggvények általánosítása
-
Tananyag
Ebben a videóban gyakorló feladatokat találsz a szögfüggvények általánosításáról tanultak ellenőrzésére. Háromszög területének kiszámítását gyakorolhatod két oldal és az általuk bezárt szög ismeretében.

Legegyszerűbb trigonometrikus egyenletek
-
Teszt
TESZT! Gyakorold be a legegyszerűbb trigonometrikus egyenletek megoldását, mert ez az alapja a nehezebb feladatok megoldásának! Figyelj a periódusra, és arra, ha több megoldás is van! Oldd meg a feladatokat önállóan! Kiértékelés után levezetjük a megoldást lépésről lépésre.
Szinusz- és koszinusz-tétel

Szinusz- és koszinusz-tétel
-
Tananyag
Ez a matematikai oktatóvideó a szinusz és koszinusz-tétel használatára tanít meg téged. Fontosak ezek a tételek, hisz minden háromszögben alkalmazhatók. Ha a háromszög oldalai és szögei közül hiányzó adatokat kell kiszámolnunk, bizonyos esetekben a szinusztételt, máskor a koszinusz-tételt kell használni. Azt is megtanulhatod a videóról, mikor melyik tételt kell használni. Kattints és nézz körül az évfolyam videói között!

Gyakorlás – szinusz- és koszinusz-tétel
-
Tananyag
Geometriai feladatokat oldunk meg, melyek megoldásával gyakorolhatod a szinusz-, és a koszinusz-tétel alkalmazását. Figyelj, mikor melyiket kell alkalmazni, melyik adat hiányzik a háromszögben.

Szinusz- és koszinusztételes feladatok
-
Teszt
TESZT! További hét feladatot oldhatsz meg önállóan a szinusz-, és a koszinusz tétel alkalmazásának gyakorlására. Kiértékelés után levezetjük a megoldást lépésről lépésre.
Trigonometrikus egyenletek, egyenlőtlenségek
Csillagaim: 0 /12

Trigonometrikus egyenletek
-
Tananyag
Ebben a videóban különböző trigonometrikus egyenletek megoldását gyakorolhatod. Bemutatjuk azokat a típusfeladatokat, amik középszinten jellemzőek, illetve igyekszünk támpontokat adni az ilyen egyenletek megoldásához. A feladatok megoldásánál feltételezzük, hogy az alapegyenletekkel (sin x = a; cos x = a; tg x; ctg x = a típusú feladatok általános megoldásával) már tisztában vagy.

Trigonometrikus egyenletek – gyakorlás
-
Tananyag
Trigonometrikus egyenletek megoldását gyakorolhatod velünk további tíz feladat megoldásával. A szinusz, koszinusz, tangens, kotangens szögfüggvények összefüggéseit alkalmazva megmutatjuk a típusfeladatokat és a megoldásuk mesterfogásait.

Trigonometrikus egyenletek
-
Teszt
TESZT! Tedd próbára tudásod! További feladatokat találsz ebben a videóban, melyekkel a trigonometrikus egyenletek megoldását gyakorolhatod. Oldd meg a feladatokat önállóan! Kiértékelés után levezetjük a megoldást lépésről lépésre.

Trigonometrikus egyenlőtlenségek
-
Tananyag
Az egyenletek után a trigonometrikus egyenlőtlenségek megoldásával is foglalkozunk. Tisztázzuk a tudnivalókat a nevezetes szögekről, meghatározzuk a tartományt, a periódust, amiben számolunk. Szinusz, koszinusz, tangens, kotangens szögfüggvényekkel is dolgozunk. Feladatokat oldunk meg a trigonometrikus egyenlőtlenségek megoldásának gyakorlására.
Trigonometria
4 alfejezet / 18 tananyag
01. Hegyesszögek szögfüggvényei
- Szögfüggvények derékszögű háromszögekben
A szögfüggvények ismerete nagyon fontos a geometriai számításokban. Derékszögű háromszögek hiányzó adatait a szinusz (sin), koszinusz (cos), tangens (tg), kotangens (ctg) szögfüggvények segítségével könnyedén kiszámíthatjuk. Nézd át mindezt ezen az interaktív oktatóvideón, és gyakorold velünk a sin, cos, tg, ctg szögfüggvények használatát!
JÁTÉK! Telepítsd be a tengeri akváriumot! Derékszögű háromszögekben keressük az alfa vagy a béta szög szögfüggvényeit. El kell döntened, hogy a felírt tört a megadott szög szinuszával, koszinuszával, vagy épp tangensével-kotangensével egyezik meg. Látni fogod utána a magyarázatot is, így a végére már magabiztosan fogod tudni használni a szögfüggvényeket.
TESZT! Hét feladat megoldásával gyakorolhatod a szögfüggvények használatát derékszögű háromszögekben. Oldd meg a feladatokat önállóan! Kiértékelés után levezetjük a megoldást lépésről lépésre.
Ez a videó a szögfüggvények alkalmazásával foglalkozik. Sorra vesszük a nevezetes (30, 45, 60 fokos) szögek szögfüggvényeit. Alkalmazzuk a szögfüggvényeket sík-és térgeometriai feladatokban.
TESZT! Feladatok segítségével tedd próbára tudásod, mennyire sikerült elsajátítanod a szögfüggvényekről tanultakat. Oldd meg a feladatokat önállóan! Kiértékelés után levezetjük a megoldást lépésről lépésre.
TESZT! Keresd a derékszögű háromszögeket, és a szögfüggvények segítségével határozd meg a hiányzó oldalakat, szögeket! Dolgozz önállóan, majd ellenőrizd a magad! Kiértékelés után láthatod a részletes megoldásokat!
02. Szögfüggvények általánosítása
- A sin x általánosítása
Ebben a matek tananyagban a szinusz szögfüggvény általánosítását vezetjük be, megnézzük a függvény tulajdonságait és a szinuszos alapegyenleteket. Azt is részletesen elmagyarázzuk, mi is az a radián, mert erre is szükség van a trigonometrikus egyenletek megoldásához.
Ebben a matek tananyagban a szinusz-függvény után a koszinusz-függvény általános definícióját, a koszinusz-függvény tulajdonságait és az ezek ismeretében megoldható egyszerű trigonometrikus egyenletek megoldását nézzük át. Feladatokkal gyakorlunk.
A tg x és ctg x alkalmazását és függvényeiket vizsgáljuk ebben a videóban. Meghatározzuk a definíciót: tg x = a megoldása; ctg x = a megoldása. Megvizsgáljuk koordináta-rendszerben is, vajon növekszik vagy csökken-e a függvény. Hol lehet értelmezni a függvényt?
Ebben a videóban gyakorló feladatokat találsz a szögfüggvények általánosításáról tanultak ellenőrzésére. Háromszög területének kiszámítását gyakorolhatod két oldal és az általuk bezárt szög ismeretében.
TESZT! Gyakorold be a legegyszerűbb trigonometrikus egyenletek megoldását, mert ez az alapja a nehezebb feladatok megoldásának! Figyelj a periódusra, és arra, ha több megoldás is van! Oldd meg a feladatokat önállóan! Kiértékelés után levezetjük a megoldást lépésről lépésre.
03. Szinusz- és koszinusz-tétel
- Szinusz- és koszinusz-tétel
Ez a matematikai oktatóvideó a szinusz és koszinusz-tétel használatára tanít meg téged. Fontosak ezek a tételek, hisz minden háromszögben alkalmazhatók. Ha a háromszög oldalai és szögei közül hiányzó adatokat kell kiszámolnunk, bizonyos esetekben a szinusztételt, máskor a koszinusz-tételt kell használni. Azt is megtanulhatod a videóról, mikor melyik tételt kell használni. Kattints és nézz körül az évfolyam videói között!
Geometriai feladatokat oldunk meg, melyek megoldásával gyakorolhatod a szinusz-, és a koszinusz-tétel alkalmazását. Figyelj, mikor melyiket kell alkalmazni, melyik adat hiányzik a háromszögben.
TESZT! További hét feladatot oldhatsz meg önállóan a szinusz-, és a koszinusz tétel alkalmazásának gyakorlására. Kiértékelés után levezetjük a megoldást lépésről lépésre.
04. Trigonometrikus egyenletek, egyenlőtlenségek
- Trigonometrikus egyenletek
Ebben a videóban különböző trigonometrikus egyenletek megoldását gyakorolhatod. Bemutatjuk azokat a típusfeladatokat, amik középszinten jellemzőek, illetve igyekszünk támpontokat adni az ilyen egyenletek megoldásához. A feladatok megoldásánál feltételezzük, hogy az alapegyenletekkel (sin x = a; cos x = a; tg x; ctg x = a típusú feladatok általános megoldásával) már tisztában vagy.
Trigonometrikus egyenletek megoldását gyakorolhatod velünk további tíz feladat megoldásával. A szinusz, koszinusz, tangens, kotangens szögfüggvények összefüggéseit alkalmazva megmutatjuk a típusfeladatokat és a megoldásuk mesterfogásait.
TESZT! Tedd próbára tudásod! További feladatokat találsz ebben a videóban, melyekkel a trigonometrikus egyenletek megoldását gyakorolhatod. Oldd meg a feladatokat önállóan! Kiértékelés után levezetjük a megoldást lépésről lépésre.
Az egyenletek után a trigonometrikus egyenlőtlenségek megoldásával is foglalkozunk. Tisztázzuk a tudnivalókat a nevezetes szögekről, meghatározzuk a tartományt, a periódust, amiben számolunk. Szinusz, koszinusz, tangens, kotangens szögfüggvényekkel is dolgozunk. Feladatokat oldunk meg a trigonometrikus egyenlőtlenségek megoldásának gyakorlására.
Számelmélet, számrendszerek
Oszthatóság, lnko, lkkt, számrendszerek

Számelmélet (1)
-
Tananyag
Összefoglaljuk a számelmélet alapjait: Osztó, oszthatóság, legnagyobb közös osztó, legkisebb közös többszörös. Beszélünk a prímszámokról, prímtényezős felbontásról, relatív prímekről. Felelevenítjük az oszthatósági szabályokat: Mikor osztható egy szám kettővel (néggyel, öttel, hárommal, nyolccal, kilenccel)? Példákkal, feladatokkal gyakorlunk.

Számrendszerek
-
Tananyag
A számelmélet alapjai után a számrendszerekről tanulunk (pl.: tizes-, kettes-, ötös alapú számrendszer). Megvizsgáljuk a számok értékét más számrendszerben. Megtanuljuk felírni a számokat különböző számrendszerekben. Megmutatjuk, milyen számokat használhatunk, melyek azok, amik nem léteznek bizonyos számrendszerekben. Példákkal, feladatokkal gyakorlunk.

Gyakorlás Számelmélet
-
Teszt
TESZT! Önálló munkára hívunk a számelmélet témában: legkisebb közös többszörös, legnagyobb közös osztó, Oszthatóság, osztási maradékok, számok átírása adott számrendszerbe. Kiértékelés után levezetjük a megoldást lépésről lépésre.
Számelmélet, számrendszerek
1 alfejezet / 3 tananyag
01. Oszthatóság, lnko, lkkt, számrendszerek
- Számelmélet (1)
Összefoglaljuk a számelmélet alapjait: Osztó, oszthatóság, legnagyobb közös osztó, legkisebb közös többszörös. Beszélünk a prímszámokról, prímtényezős felbontásról, relatív prímekről. Felelevenítjük az oszthatósági szabályokat: Mikor osztható egy szám kettővel (néggyel, öttel, hárommal, nyolccal, kilenccel)? Példákkal, feladatokkal gyakorlunk.
A számelmélet alapjai után a számrendszerekről tanulunk (pl.: tizes-, kettes-, ötös alapú számrendszer). Megvizsgáljuk a számok értékét más számrendszerben. Megtanuljuk felírni a számokat különböző számrendszerekben. Megmutatjuk, milyen számokat használhatunk, melyek azok, amik nem léteznek bizonyos számrendszerekben. Példákkal, feladatokkal gyakorlunk.
TESZT! Önálló munkára hívunk a számelmélet témában: legkisebb közös többszörös, legnagyobb közös osztó, Oszthatóság, osztási maradékok, számok átírása adott számrendszerbe. Kiértékelés után levezetjük a megoldást lépésről lépésre.
Exp. és logaritm.
Hatvány, gyök
Csillagaim: 0 /21

Hatványozás (ismétlés)
-
Tananyag
A hatványozás, a gyökvonás és a logaritmus összefüggenek egymással. A hatványozás az alapja mindennek, tehát nagyon fontos, hogy tisztában legyél ezek azonosságaival, és alkalmazni is tudd őket. Átismételjük a hatványozást egész kitevővel. Meghatározzuk a hatványozás definícióját, a hatványozás azonosságait. Feladatokat oldunk meg együtt a hatványozás gyakorlására.

Négyzetgyök (ismétlés)
-
Tananyag
A négyzetgyök fogalmával már korábban is találkozhattál. Sorra vesszük a négyzetgyök átalakítás azonosságait. Megvizsgáljuk, mit lehet “kihozni”, kiemelni a gyökjel alól, vagy mi lehet bevinni a gyökjel alá. A törtek (nevező) gyöktelenítéséről is tanulunk. Példákat, feladatokat oldunk meg gyökvonással kapcsolatban. Ismételjük át mindezt a 10.-es anyagból!

n-edik gyök
-
Tananyag
A gyökvonás nemcsak négyzetgyököt jelenthet. Megvizsgáljuk, mit is jelent a 3., 4., stb. gyök, hogyan lehet számolni vele. Mi történik páros és páratlan n szám esetén, megnézzük, milyen feltételeknek kell megfelelni. Az n-dik gyökvonás azonosságaival is foglalkozunk. Hozzuk közös gyökjel alá! A gyökök kitevőit is össze lehet szorozni, mint a hatványkitevőket.

n-edik gyök, törtkitevős hatvány
-
Tananyag
A mostani matekvideóban először is az n-edik gyök fogalmát ismételjük át, példákkal, foglalkozunk a páros és páratlan gyök közötti különbségekkel. Aztán megnézzük, mit jelent az, ha a hatvány kitevőjében egy törtszám áll. Majd megmutatjuk, hogy így egyesítve a gyökvonást a hatványozással, mennyivel könnyebb a törtkitevőkkel műveleteket végezni.

n-edik gyök, törtkitevős hatvány – gyakorlás
-
Tananyag
Gyakoroljuk a gyökös és törtkitevős hatványok átalakítását. Alkalmazd a hatványozás és a gyökvonás azonosságait és hozd egyszerűbb alakra a kifejezéseket!

Törtkitevős hatvány
-
Játék
JÁTÉK! Építs fel és rendezz be egy modern családi házat! A törtkitevős hatványok értelmezését, átalakítását gyakorolhatod a feladatokkal. Döntsd el, hogy helyes-e a számolás vagy átalakítás eredménye. Utána látni fogod a magyarázatot is. Mire elkészül a ház, profin fogsz bánni a törtkitevős hatványokkal.

Törtkitevős hatvány
-
Teszt
TESZT! A hatványozásról és a gyökvonásról tanultakat gyakorolhatod a feladatok megoldásával. Oldd meg a feladatokat önállóan! Kiértékelés után levezetjük a megoldást lépésről lépésre.
Exponenciális egyenletek, exp.-log. függvények
Csillagaim: 0 /12

Exponenciális egyenletek
-
Tananyag
Ha jól tudod a hatványozás azonosságait, akkor az exponenciális egyenletek megoldása is menni fog. Nézzük meg ennek lépéseit, a típusfeladatokat, és gyakoroljuk ezek megoldását! Sok gyakorló példa vár.

Exponenciális egyenletek
-
Játék
JÁTÉK! Oldd meg az exponenciális egyenleteket, és szerezd meg az elsüllyedt hajók kincseit! Vizsgáld meg minden lépésben, hogy jó-e a levezetés, helyes-e az átalakítás.

Exponenciális egyenletek
-
Teszt
TESZT! Oldd meg a következő exponenciális egyenleteket a valós számok halmazán! Dolgozz önállóan, kiderül, elsajátítottad-e az exponenciális egyenletekről szóló tudnivalókat. Kiértékelés után levezetjük a megoldást lépésről lépésre.

Exp. és log. függvények
-
Tananyag
Exponenciális és a logaritmus függvények legfontosabb tulajdonságait tekintjük át ezen a videón. Vajon hogyan néz ki a függvény 1-nél kisebb és 1-nél nagyobb számok esetén. Csökkenő vagy növekvő a függvény? A függvények értelmezési tartománya a valós számok halmaza, az értékkészlet viszont csak a pozitív számok halmaza.
Logaritmus, logaritmikus egyenletek
Csillagaim: 0 /18

Logaritmus
-
Tananyag
A logaritmus művelete sok szempontból a legnehezebb fogalmak közé tartozik a középszintű matematikában. Ez a videó úgy mutatja be a logaritmus definícióját, és az ehhez kapcsolódó feladatokat, hogy az emészthető legyen bárki számára. Hogyan kell “levarázsolni” a hatvány kitevőjét, aztán hogyan kell áttérni más alapra, ilyeneket is begyakorolhatsz ezzel a videóval.

Logaritmus alapjai
-
Teszt
TESZT! Tesztelt a tudásod az alábbi feladatokkal: Határozd meg a logaritmusok értékeit!; Oldd meg a logaritmusos egyenleteket!; Számítsd ki a közelítő értékét! Sok sikert! Kiértékelés után levezetjük a megoldást lépésről lépésre.

Logaritmikus egyenletek
-
Tananyag
Ez a matematikai oktatóvideó a logaritmikus egyenletek (vagy logaritmusos egyenletek) különböző fajtáit mutatja be. Sorra vesszük a logaritmus azonosságait, és gyakorolhatod is a feladatmegoldást.

Logaritmus azonosságok
-
Teszt
TESZT! Oldd meg a feladatokat a logaritmus-azonosságok alkalmazásával! Logaritmusos matematika feladatok megoldását gyakorolhatod önállóan, majd kiértékelés után levezetjük a megoldást lépésről lépésre.

Logaritmus gyakorlása
-
Játék
JÁTÉK! Építsd fel a városodat a mezőre! El kell döntened a logaritmusokról, vagy a velük végzett műveletekről, hogy az átalakítás helyes vagy helytelen. Látni fogod utána a magyarázatot is. Így a végére profin tudsz majd bánni a logaritmussal és az azonosságaival.
Logaritmikus egyenletek
-
Teszt
TESZT! Tedd próbára tudásod! Add meg a következő logaritmikus egyenletek megoldásait logaritmus azonosságok felhasználásával! Kiértékelés után levezetjük a megoldást lépésről lépésre.
Exp. és log. egyenlőtlenségek, gyakorlás

Exp és log egyenlőtlenségek
-
Tananyag
Ez a videó az exponenciális és a logaritmikus egyenlőtlenségek megoldásának rejtelmeibe vezet be. Növekvő vagy csökkenő a függvény? Melyik hatvány a nagyobb? Hogyan változik a relációs jel? Feladatokat oldunk meg exponenciális és logaritmikus egyenlőtlenségekkel.

Logaritmus felmérő
-
Teszt
TESZT! Az alábbi tesztben próbára teheted tudásod a logaritmus definíció és logaritmus azonosságok alkalmazása, logaritmikus egyenletek, egyenlőtlenségek, egyenlet-rendszerek és a logaritmus függvény ábrázolása terén. Dolgozz önállóan, majd a kiértékelésben levezetjük a megoldást lépésről lépésre.

Gyakorlás Exponenciális feladatok
-
Teszt
TESZT! Tedd próbára tudásod az exponenciális egyenleteket, egyenlőtlenségeket terén! Ábrázold koordináta-rendszerben a függvényt! Dolgozz önállóan, majd a kiértékelés során levezetjük a megoldást lépésről lépésre.
Exp. és logaritm.
4 alfejezet / 20 tananyag
01. Hatvány, gyök
- Hatványozás (ismétlés)
A hatványozás, a gyökvonás és a logaritmus összefüggenek egymással. A hatványozás az alapja mindennek, tehát nagyon fontos, hogy tisztában legyél ezek azonosságaival, és alkalmazni is tudd őket. Átismételjük a hatványozást egész kitevővel. Meghatározzuk a hatványozás definícióját, a hatványozás azonosságait. Feladatokat oldunk meg együtt a hatványozás gyakorlására.
A négyzetgyök fogalmával már korábban is találkozhattál. Sorra vesszük a négyzetgyök átalakítás azonosságait. Megvizsgáljuk, mit lehet “kihozni”, kiemelni a gyökjel alól, vagy mi lehet bevinni a gyökjel alá. A törtek (nevező) gyöktelenítéséről is tanulunk. Példákat, feladatokat oldunk meg gyökvonással kapcsolatban. Ismételjük át mindezt a 10.-es anyagból!
A gyökvonás nemcsak négyzetgyököt jelenthet. Megvizsgáljuk, mit is jelent a 3., 4., stb. gyök, hogyan lehet számolni vele. Mi történik páros és páratlan n szám esetén, megnézzük, milyen feltételeknek kell megfelelni. Az n-dik gyökvonás azonosságaival is foglalkozunk. Hozzuk közös gyökjel alá! A gyökök kitevőit is össze lehet szorozni, mint a hatványkitevőket.
A mostani matekvideóban először is az n-edik gyök fogalmát ismételjük át, példákkal, foglalkozunk a páros és páratlan gyök közötti különbségekkel. Aztán megnézzük, mit jelent az, ha a hatvány kitevőjében egy törtszám áll. Majd megmutatjuk, hogy így egyesítve a gyökvonást a hatványozással, mennyivel könnyebb a törtkitevőkkel műveleteket végezni.
Gyakoroljuk a gyökös és törtkitevős hatványok átalakítását. Alkalmazd a hatványozás és a gyökvonás azonosságait és hozd egyszerűbb alakra a kifejezéseket!
JÁTÉK! Építs fel és rendezz be egy modern családi házat! A törtkitevős hatványok értelmezését, átalakítását gyakorolhatod a feladatokkal. Döntsd el, hogy helyes-e a számolás vagy átalakítás eredménye. Utána látni fogod a magyarázatot is. Mire elkészül a ház, profin fogsz bánni a törtkitevős hatványokkal.
TESZT! A hatványozásról és a gyökvonásról tanultakat gyakorolhatod a feladatok megoldásával. Oldd meg a feladatokat önállóan! Kiértékelés után levezetjük a megoldást lépésről lépésre.
02. Exponenciális egyenletek, exp.-log. függvények
- Exponenciális egyenletek
Ha jól tudod a hatványozás azonosságait, akkor az exponenciális egyenletek megoldása is menni fog. Nézzük meg ennek lépéseit, a típusfeladatokat, és gyakoroljuk ezek megoldását! Sok gyakorló példa vár.
JÁTÉK! Oldd meg az exponenciális egyenleteket, és szerezd meg az elsüllyedt hajók kincseit! Vizsgáld meg minden lépésben, hogy jó-e a levezetés, helyes-e az átalakítás.
TESZT! Oldd meg a következő exponenciális egyenleteket a valós számok halmazán! Dolgozz önállóan, kiderül, elsajátítottad-e az exponenciális egyenletekről szóló tudnivalókat. Kiértékelés után levezetjük a megoldást lépésről lépésre.
Exponenciális és a logaritmus függvények legfontosabb tulajdonságait tekintjük át ezen a videón. Vajon hogyan néz ki a függvény 1-nél kisebb és 1-nél nagyobb számok esetén. Csökkenő vagy növekvő a függvény? A függvények értelmezési tartománya a valós számok halmaza, az értékkészlet viszont csak a pozitív számok halmaza.
03. Logaritmus, logaritmikus egyenletek
A logaritmus művelete sok szempontból a legnehezebb fogalmak közé tartozik a középszintű matematikában. Ez a videó úgy mutatja be a logaritmus definícióját, és az ehhez kapcsolódó feladatokat, hogy az emészthető legyen bárki számára. Hogyan kell “levarázsolni” a hatvány kitevőjét, aztán hogyan kell áttérni más alapra, ilyeneket is begyakorolhatsz ezzel a videóval.
TESZT! Tesztelt a tudásod az alábbi feladatokkal: Határozd meg a logaritmusok értékeit!; Oldd meg a logaritmusos egyenleteket!; Számítsd ki a közelítő értékét! Sok sikert! Kiértékelés után levezetjük a megoldást lépésről lépésre.
Ez a matematikai oktatóvideó a logaritmikus egyenletek (vagy logaritmusos egyenletek) különböző fajtáit mutatja be. Sorra vesszük a logaritmus azonosságait, és gyakorolhatod is a feladatmegoldást.
TESZT! Oldd meg a feladatokat a logaritmus-azonosságok alkalmazásával! Logaritmusos matematika feladatok megoldását gyakorolhatod önállóan, majd kiértékelés után levezetjük a megoldást lépésről lépésre.
JÁTÉK! Építsd fel a városodat a mezőre! El kell döntened a logaritmusokról, vagy a velük végzett műveletekről, hogy az átalakítás helyes vagy helytelen. Látni fogod utána a magyarázatot is. Így a végére profin tudsz majd bánni a logaritmussal és az azonosságaival.
TESZT! Tedd próbára tudásod! Add meg a következő logaritmikus egyenletek megoldásait logaritmus azonosságok felhasználásával! Kiértékelés után levezetjük a megoldást lépésről lépésre.
04. Exp. és log. egyenlőtlenségek, gyakorlás
- Exp és log egyenlőtlenségek
Ez a videó az exponenciális és a logaritmikus egyenlőtlenségek megoldásának rejtelmeibe vezet be. Növekvő vagy csökkenő a függvény? Melyik hatvány a nagyobb? Hogyan változik a relációs jel? Feladatokat oldunk meg exponenciális és logaritmikus egyenlőtlenségekkel.
TESZT! Az alábbi tesztben próbára teheted tudásod a logaritmus definíció és logaritmus azonosságok alkalmazása, logaritmikus egyenletek, egyenlőtlenségek, egyenlet-rendszerek és a logaritmus függvény ábrázolása terén. Dolgozz önállóan, majd a kiértékelésben levezetjük a megoldást lépésről lépésre.
TESZT! Tedd próbára tudásod az exponenciális egyenleteket, egyenlőtlenségeket terén! Ábrázold koordináta-rendszerben a függvényt! Dolgozz önállóan, majd a kiértékelés során levezetjük a megoldást lépésről lépésre.
Egyenletrendszerek
Egyenletrendszerek megoldása

Elsőfokú egyenletrendszerek
-
Tananyag
Elsőfokú egyenletrendszerek megoldási módszereit ismertetjük. Kifejezzük az egyik ismeretlent az egyik egyenletből, majd visszahelyettesítjük a másik egyenletbe. Másik módszer az egyenlő együtthatók módszere. Továbbá lehetséges az új ismeretlen bevezetése is. Tarts velünk, biztos megérted Te is!
Másodfokú és egyéb egyenletrendszerek
-
Tananyag
Másodfokú, logaritmusos és trigonometrikus egyenletrendszerek megoldásának lépéseit, módszereit sajátíthatod el ebben a videóban. Fejezzük ki az egyik egyenletből az egyik ismeretlent, majd helyettesítsük be a másik egyenletbe!

Gyakorlás: trig. és exp-log egyenletrendszerek
-
Tananyag
Tovább gyakorolhatod az exponenciális, logaritmikus-, és trigonometrikus egyenletrendszerek megoldását. Sok gyakorló feladatot oldunk meg együtt.
Egyenletrendszerek
1 alfejezet / 3 tananyag
01. Egyenletrendszerek megoldása
- Elsőfokú egyenletrendszerek
Elsőfokú egyenletrendszerek megoldási módszereit ismertetjük. Kifejezzük az egyik ismeretlent az egyik egyenletből, majd visszahelyettesítjük a másik egyenletbe. Másik módszer az egyenlő együtthatók módszere. Továbbá lehetséges az új ismeretlen bevezetése is. Tarts velünk, biztos megérted Te is!
Másodfokú, logaritmusos és trigonometrikus egyenletrendszerek megoldásának lépéseit, módszereit sajátíthatod el ebben a videóban. Fejezzük ki az egyik egyenletből az egyik ismeretlent, majd helyettesítsük be a másik egyenletbe!
Tovább gyakorolhatod az exponenciális, logaritmikus-, és trigonometrikus egyenletrendszerek megoldását. Sok gyakorló feladatot oldunk meg együtt.
Koordinátageometria
Alapok

Vektorok (ismétlés)
-
Tananyag
A vektorok irányított szakaszok. Először azokat a vektorokkal kapcsolatos ismereteket nézzük át, amelyekkel valószínűleg már találkoztál. Vektorműveleteket végzünk, vektorokat adunk össze és vonunk ki egymásból, vektort számmal szorzunk összefűzés, paralelogramma módszerével. Elmondjuk, mikor melyik módszert érdemes vagy kell alkalmazni. Megismerkedünk a helyvektor és a háromszög súlypontjába mutató helyvektor fogalmával. Vektoros feladatokat oldunk meg együtt.
Alapok
-
Tananyag
A koordinátageometria tanulását ezekkel az alapokkal kell kezdeni. Ezen a videón mindent megtanítunk a vektorokkal kapcsolatos számításokról: vektor hossza, vektorműveletek koordinátákkal, vektorok hajlásszöge, skaláris szorzata. Ezen túl megmutatjuk még, hogyan kell kiszámolni szakasz hosszát, szakasz felezőpontját, a harmadolópontjait, sőt, még a háromszög súlypontjának koordinátáiról is szó van ebben a tananyagban.

Koordinátageometria alapok
-
Teszt
TESZT! Számítsd ki két pont távolságát! Mennyi a vektor hossza? Írd fel a háromszög súlypontjának koordinátáit! Mennyi a b és c vektor skaláris szorzata? Írd fel a paralelogramma oldalvektorait! Dolgozz önállóan! Kiértékelés után levezetjük a megoldást lépésről lépésre.
Egyenes egyenlete

Egyenes egyenlete
-
Tananyag
Az egyenessel kapcsolatos alapfogalmakat vesszük át ezen a videón: irányvektor, normálvektor, irányszög, meredekség vagy iránytangens. Szó lesz az egyenes normálvektoros egyenletéről, a párhuzamos és merőleges egyenesekről, háromszögek nevezetes vonalainak egyenletéről, egyenesek metszéspontjáról.

Egyenes egyenlete
-
Teszt
TESZT! Gyakorló feladatokat találsz ebben a videóban: Mennyi az egyenes meredeksége? Írd fel a P és Q pontokon átmenő egyenes egyenletét! Írd fel a C csúcson átmenő magasságvonal egyenletét! Határozd meg a két egyenes metszéspontját!
Kör egyenlete

Kör egyenlete
-
Tananyag
Ebben a videóban a kör egyenletével ismerkedhetsz meg. Megtanulhatod, hogyan kell felírni a kör egyenletét, visszafelé: hogyan lehet az egyenletből kiszámítani a középpont koordinátáit és a sugarát. Hogyan kell felírni a kör érintőjének egyenletét, kiszámítani körök és egyenesek metszéspontjait. Kattints és nézz körül az évfolyam videói között!

Kör egyenlete
-
Teszt
TESZT! Gyakorló feladatokat találsz ebben a videóban: Írd fel a kör egyenletét! Rajta van-e a k körön a P pont? Dolgozz önállóan! Kiértékelés után levezetjük a megoldást lépésről lépésre.
Gyakorlás
Csillagaim: 0 /15

Gyakorlás 1.: Alapfeladatok
-
Tananyag
Írd fel az A és B pontokon átmenő egyenes egyenletét! Írd fel az ABC háromszög mb magasságvonalának egyenletét! Írd fel az AB átmérőjű kör egyenletét! Számítsd ki a k kör és az mb metszéspontjának (metszéspontjainak) koordinátáit!
Gyakorlás 2.: Összetett feladatok /a
-
Tananyag
Olyan matematika feladatokat oldunk meg, melyekben szükség van az elemi geometriai és a koordináta geometriai ismereteinkre is: háromszöggel és paralelogrammával kapcsolatos feladatok várnak.

Gyakorlás 3.: Összetett feladatok /b
-
Tananyag
Újabb koordináta geometriai feladatok várnak: körrel, háromszöggel, négyszöggel kapcsolatos koordináta geometriai kérdéseket kell megválaszolni. Oldjuk meg együtt ezeket az összetett feladatokat!

Gyakorlás Koordinátageometria I.
-
Teszt
TESZT! Önálló munkára hívunk. A koordinátageometriából tanult ismeretek alkalmazását gyakorolhatod a három-, és négyszögekkel kapcsolatos feladatok megoldásával. Kiértékelés után levezetjük a megoldást lépésről lépésre.

Gyakorlás Koordinátageometria II.
-
Teszt
TESZT! További koordinátageometriai feladatok gyakorláshoz; Írd fel az AB átmérőjű kör egyenletét! Írd fel a kör érintőjének egyenletét! Határozd meg a körök metszéspontjainak a koordinátáit!
Koordinátageometria
4 alfejezet / 12 tananyag
01. Alapok
- Vektorok (ismétlés)
A vektorok irányított szakaszok. Először azokat a vektorokkal kapcsolatos ismereteket nézzük át, amelyekkel valószínűleg már találkoztál. Vektorműveleteket végzünk, vektorokat adunk össze és vonunk ki egymásból, vektort számmal szorzunk összefűzés, paralelogramma módszerével. Elmondjuk, mikor melyik módszert érdemes vagy kell alkalmazni. Megismerkedünk a helyvektor és a háromszög súlypontjába mutató helyvektor fogalmával. Vektoros feladatokat oldunk meg együtt.
A koordinátageometria tanulását ezekkel az alapokkal kell kezdeni. Ezen a videón mindent megtanítunk a vektorokkal kapcsolatos számításokról: vektor hossza, vektorműveletek koordinátákkal, vektorok hajlásszöge, skaláris szorzata. Ezen túl megmutatjuk még, hogyan kell kiszámolni szakasz hosszát, szakasz felezőpontját, a harmadolópontjait, sőt, még a háromszög súlypontjának koordinátáiról is szó van ebben a tananyagban.
TESZT! Számítsd ki két pont távolságát! Mennyi a vektor hossza? Írd fel a háromszög súlypontjának koordinátáit! Mennyi a b és c vektor skaláris szorzata? Írd fel a paralelogramma oldalvektorait! Dolgozz önállóan! Kiértékelés után levezetjük a megoldást lépésről lépésre.
02. Egyenes egyenlete
- Egyenes egyenlete
Az egyenessel kapcsolatos alapfogalmakat vesszük át ezen a videón: irányvektor, normálvektor, irányszög, meredekség vagy iránytangens. Szó lesz az egyenes normálvektoros egyenletéről, a párhuzamos és merőleges egyenesekről, háromszögek nevezetes vonalainak egyenletéről, egyenesek metszéspontjáról.
TESZT! Gyakorló feladatokat találsz ebben a videóban: Mennyi az egyenes meredeksége? Írd fel a P és Q pontokon átmenő egyenes egyenletét! Írd fel a C csúcson átmenő magasságvonal egyenletét! Határozd meg a két egyenes metszéspontját!
03. Kör egyenlete
Ebben a videóban a kör egyenletével ismerkedhetsz meg. Megtanulhatod, hogyan kell felírni a kör egyenletét, visszafelé: hogyan lehet az egyenletből kiszámítani a középpont koordinátáit és a sugarát. Hogyan kell felírni a kör érintőjének egyenletét, kiszámítani körök és egyenesek metszéspontjait. Kattints és nézz körül az évfolyam videói között!
TESZT! Gyakorló feladatokat találsz ebben a videóban: Írd fel a kör egyenletét! Rajta van-e a k körön a P pont? Dolgozz önállóan! Kiértékelés után levezetjük a megoldást lépésről lépésre.
04. Gyakorlás
- Gyakorlás 1.: Alapfeladatok
Írd fel az A és B pontokon átmenő egyenes egyenletét! Írd fel az ABC háromszög mb magasságvonalának egyenletét! Írd fel az AB átmérőjű kör egyenletét! Számítsd ki a k kör és az mb metszéspontjának (metszéspontjainak) koordinátáit!
Olyan matematika feladatokat oldunk meg, melyekben szükség van az elemi geometriai és a koordináta geometriai ismereteinkre is: háromszöggel és paralelogrammával kapcsolatos feladatok várnak.
Újabb koordináta geometriai feladatok várnak: körrel, háromszöggel, négyszöggel kapcsolatos koordináta geometriai kérdéseket kell megválaszolni. Oldjuk meg együtt ezeket az összetett feladatokat!
TESZT! Önálló munkára hívunk. A koordinátageometriából tanult ismeretek alkalmazását gyakorolhatod a három-, és négyszögekkel kapcsolatos feladatok megoldásával. Kiértékelés után levezetjük a megoldást lépésről lépésre.
TESZT! További koordinátageometriai feladatok gyakorláshoz; Írd fel az AB átmérőjű kör egyenletét! Írd fel a kör érintőjének egyenletét! Határozd meg a körök metszéspontjainak a koordinátáit!
Kombinatorika, gráfok, valószínűség
Kombinatorika, gráfok
Csillagaim: 0 /15

I. Permutációk és variációk
-
Tananyag
A kombinatorika újabb módszereivel foglalkozunk. A permutációk (= sorbarendezések): n különböző elem összes lehetséges sorrendje, a variációk: k különböző hely n különböző elemmel való kombinálása. Sok érdekes feladat vár.

II. Kombinációk és vegyes feladatok
-
Tananyag
Példákkal gyakorolhatod a kombinációkat (= n elem ismétlés nélküli kombinációi). Megtanuljuk eldönteni, hogy a feladatban variációról vagy kombinációról van-e szó. Vegyes feladatokat oldunk meg permutáció, variáció, kombináció témában. Tarts velünk!

Gyakorlás Kombinatorika
-
Teszt
TESZT! Gyakorlófeladatok önálló megoldására hívunk a kombinatorika témaköréből: Hányféle sorrend/megoldás lehetséges? Kiértékelés után levezetjük a megoldást lépésről lépésre.

Gráfok
-
Tananyag
Megismerkedünk a gráfok fogalmával, pontjaival, éleivel, és a köztük lévő összefüggésekkel. Megtanuljuk a gráf készítését. Feladatokat oldunk meg a gráfok témaköréből, gráfok segítségével.

Gráfok
-
Teszt
TESZT! Ellenőrizd a tudásod! Rajzolj gráfokat, állapítsd meg, hogy lehet-e adott fokszámú gráfot rajzolni, számítsd ki a teljes gráf éleinek számát, szemléltesd gráfokkal a szöveges feladatokat.
Valószínűségszámítás
Csillagaim: 0 /15

Valószínűségszámítás, eseményalgebra (10. oszt.)
-
Tananyag
Ezen a videón a valószínűségszámítás alapjaival ismerkedhetsz meg. A klasszikus valószínűségi modellel, az alkalmazásával, egy kis eseményalgebrával, események összegének és szorzatának valószínűségével, komplementer események valószínűségével. Példák és gyakorlófeladatok teszik lehetővé, hogy ellenőrizd magadat. további gyakorlófeladatokat pedig a fejezet következő videóján találsz.

Valószínűségszámítás I.
-
Tananyag
A valószínűségszámítás alapja a klasszikus valószínűségi modell. A kedvező esetek számát osztjuk az összes eset számával. Másik típus a visszatevéses mintavétel. Beszélünk még a geometriai valószínűségről. Megvizsgálhatjuk, milyen esetekben melyik típus alkalmazható.Gyakorló feladatokat oldunk meg együtt.

Valószínűségszámítás II. – gyakorlófeladatok
-
Tananyag
Gyakorló feladatokat oldunk meg együtt: Mekkora az esélye, hogy lányt választunk? Mekkora a valószínűsége, hogy elsőre sárgát, aztán kéket és végül pirosat húzunk? Mekkora a valószínűsége, hogy mindkét kockával 6-ost dobunk?

Valószínűségszámítás III. Mintavételek valószínűsége
-
Tananyag
Az új követelményekben a mintavételek valószínűsége külön hangsúlyosan szerepel. Ebben a videóban ezt könnyen megtanulhatod, részletesen kitérünk a visszatevés nélküli és a visszatevéses mintavételre is, valamint a binomiális eloszlásra. Találsz olyan mintavételtől független feladatokat is, ahol alkalmazhatók ezek az ismeretek.

Gyakorlás Valószínűségszámítás
-
Teszt
TESZT! Önálló munkára hívunk. Feladatok megoldásával gyakorolhatod a valószínűségszámításból szerzett ismereteidet, tudásodat. Kiértékelés után levezetjük a megoldást lépésről lépésre.
Kombinatorika, gráfok, valószínűség
2 alfejezet / 10 tananyag
01. Kombinatorika, gráfok
- I. Permutációk és variációk
A kombinatorika újabb módszereivel foglalkozunk. A permutációk (= sorbarendezések): n különböző elem összes lehetséges sorrendje, a variációk: k különböző hely n különböző elemmel való kombinálása. Sok érdekes feladat vár.
Példákkal gyakorolhatod a kombinációkat (= n elem ismétlés nélküli kombinációi). Megtanuljuk eldönteni, hogy a feladatban variációról vagy kombinációról van-e szó. Vegyes feladatokat oldunk meg permutáció, variáció, kombináció témában. Tarts velünk!
TESZT! Gyakorlófeladatok önálló megoldására hívunk a kombinatorika témaköréből: Hányféle sorrend/megoldás lehetséges? Kiértékelés után levezetjük a megoldást lépésről lépésre.
Megismerkedünk a gráfok fogalmával, pontjaival, éleivel, és a köztük lévő összefüggésekkel. Megtanuljuk a gráf készítését. Feladatokat oldunk meg a gráfok témaköréből, gráfok segítségével.
TESZT! Ellenőrizd a tudásod! Rajzolj gráfokat, állapítsd meg, hogy lehet-e adott fokszámú gráfot rajzolni, számítsd ki a teljes gráf éleinek számát, szemléltesd gráfokkal a szöveges feladatokat.
02. Valószínűségszámítás
- Valószínűségszámítás, eseményalgebra (10. oszt.)
Ezen a videón a valószínűségszámítás alapjaival ismerkedhetsz meg. A klasszikus valószínűségi modellel, az alkalmazásával, egy kis eseményalgebrával, események összegének és szorzatának valószínűségével, komplementer események valószínűségével. Példák és gyakorlófeladatok teszik lehetővé, hogy ellenőrizd magadat. további gyakorlófeladatokat pedig a fejezet következő videóján találsz.
A valószínűségszámítás alapja a klasszikus valószínűségi modell. A kedvező esetek számát osztjuk az összes eset számával. Másik típus a visszatevéses mintavétel. Beszélünk még a geometriai valószínűségről. Megvizsgálhatjuk, milyen esetekben melyik típus alkalmazható.Gyakorló feladatokat oldunk meg együtt.
Gyakorló feladatokat oldunk meg együtt: Mekkora az esélye, hogy lányt választunk? Mekkora a valószínűsége, hogy elsőre sárgát, aztán kéket és végül pirosat húzunk? Mekkora a valószínűsége, hogy mindkét kockával 6-ost dobunk?
Az új követelményekben a mintavételek valószínűsége külön hangsúlyosan szerepel. Ebben a videóban ezt könnyen megtanulhatod, részletesen kitérünk a visszatevés nélküli és a visszatevéses mintavételre is, valamint a binomiális eloszlásra. Találsz olyan mintavételtől független feladatokat is, ahol alkalmazhatók ezek az ismeretek.
TESZT! Önálló munkára hívunk. Feladatok megoldásával gyakorolhatod a valószínűségszámításból szerzett ismereteidet, tudásodat. Kiértékelés után levezetjük a megoldást lépésről lépésre.
Statisztika
Alapfogalmak, grafikonok értelmezése, készítése
Csillagaim: 0 /15
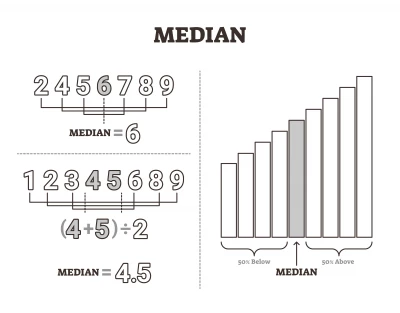
Átlag, medián, módusz
-
Tananyag
A statisztika alapjait ismételjük át. Megtanuljuk, mik azok a középértékek. Hogyan számoljuk ki az átlagot, mediánt, móduszt? Az adatok osztályba sorolásáról lesz szó. Példákat, feladatokat oldunk meg az átlag, módusz, medián értékének meghatározására.

Terjedelem, szórás
-
Tananyag
Az adathalmazok fontos jellemzőit vesszük sorra: terjedelem, átlagos abszolút eltérés és szórás. Nem mindegy, hogy a halmaz csak egymáshoz nagyon közeli értékeket tartalmaz, vagy vannak elszórt értékek is. Megvizsgáljuk, mi a szórásnégyzet. Feladatokat oldunk meg a terjedelem, átlagos abszolút eltérés és szórás kiszámítására.

Grafikonok értelmezése
-
Tananyag
A statisztikai eredményeket grafikusan is kiértékelhetjük. A különböző grafikonokat mutatjuk be: kördiagram, hisztogram, sávdiagram, oszlopdiagram. Megtanuljuk értelmezni a grafikonokat, leolvasni az adatokat a grafikonról.

Grafikonok (diagramok) készítése
-
Tananyag
Megmutatjuk, hogyan kell oszlop-, sáv-, és kördiagramot készíteni a rendelkezésünkre álló adatokból. Ezen az interaktív oktatóvideón összefoglaljuk mindazt, amit középszinten tudni kell a grafikonok készítéséről. Hogyan kell oszlopdiagramot készíteni, mennyiben más a sávdiagram, és mi a titka a kördiagramok készítésének.

Statisztika
-
Teszt
TESZT! Tedd próbára tudásod a statisztikából tanultakról: átlag, módusz, medián meghatározása, adatok leolvasása diagramról, diagramkészítés. Oldd meg a feladatokat önállóan! Kiértékelés után levezetjük a megoldást lépésről lépésre.
Statisztika
1 alfejezet / 5 tananyag
01. Alapfogalmak, grafikonok értelmezése, készítése
- Átlag, medián, módusz
A statisztika alapjait ismételjük át. Megtanuljuk, mik azok a középértékek. Hogyan számoljuk ki az átlagot, mediánt, móduszt? Az adatok osztályba sorolásáról lesz szó. Példákat, feladatokat oldunk meg az átlag, módusz, medián értékének meghatározására.
Az adathalmazok fontos jellemzőit vesszük sorra: terjedelem, átlagos abszolút eltérés és szórás. Nem mindegy, hogy a halmaz csak egymáshoz nagyon közeli értékeket tartalmaz, vagy vannak elszórt értékek is. Megvizsgáljuk, mi a szórásnégyzet. Feladatokat oldunk meg a terjedelem, átlagos abszolút eltérés és szórás kiszámítására.
A statisztikai eredményeket grafikusan is kiértékelhetjük. A különböző grafikonokat mutatjuk be: kördiagram, hisztogram, sávdiagram, oszlopdiagram. Megtanuljuk értelmezni a grafikonokat, leolvasni az adatokat a grafikonról.
Megmutatjuk, hogyan kell oszlop-, sáv-, és kördiagramot készíteni a rendelkezésünkre álló adatokból. Ezen az interaktív oktatóvideón összefoglaljuk mindazt, amit középszinten tudni kell a grafikonok készítéséről. Hogyan kell oszlopdiagramot készíteni, mennyiben más a sávdiagram, és mi a titka a kördiagramok készítésének.
TESZT! Tedd próbára tudásod a statisztikából tanultakról: átlag, módusz, medián meghatározása, adatok leolvasása diagramról, diagramkészítés. Oldd meg a feladatokat önállóan! Kiértékelés után levezetjük a megoldást lépésről lépésre.
Analízis
Sorozatok határértéke
Csillagaim: 0 /12

Definíciók, alapok
-
Tananyag
Megvizsgáljuk a korlátos sorozatokat, az alsó-felső korlátot. Sorozatok monotonitásáról tanulunk: a szigorúan monoton csökkenő és növekvő sorozatokról. Megtanuljuk, mi a konvergencia, mitől konvergens a sorozat, és mit nevezünk a sorozat határértékének. Példákat, feladatokat oldunk meg sorozatokra.

Tételek, végtelenhez tartó sorozatok
-
Tananyag
A határérték számításhoz kapcsolódó tételek bizonyítására kerül sor ezen a videón: sorozatok összegére, különbségére, szorzatára, hányadosára vonatkozó tételek. Gyakoroljuk a határérték számítást példákkal, feladatokkal. Megvizsgáljuk a végtelenbe tartó sorozatokat. Ezek a valódi divergens sorozatok.

Fontosabb sorozatok
-
Tananyag
Nevezetes sorozatok határértékéről lesz szó. Megvizsgáljuk és bizonyítjuk a nevezetes sorozatok tételeit. Beszélünk a Bernoulli egyenlőtlenség, és megtudhatod azt is, mi az a rendőr elv (közrefogási elv). Példákkal, feladatokkal gyakorlunk.
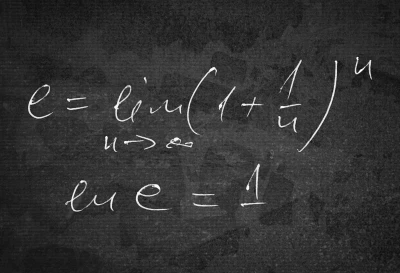
Sorozatok határértéke – gyakorlás
-
Tananyag
Ebben a videóban olyan feladatokat gyűjtöttünk össze, melyek megoldásával gyakorolhatod a sorozatok határértékének kiszámítását. Sok szép feladat vár. Határozd meg a sorozatok határértékét!
Függvények határértéke, folytonossága
Csillagaim: 0 /12

Definíciók, alapok
-
Tananyag
Függvények határértékéről, függvények folytonosságáról tanulunk. Mikor folytonos és mikor nem folytonos egy függvény? Függvények összegének, különbségének, szorzatának, hányadosának határértékét vizsgáljuk. Példákat, feladatokat oldunk meg függvény határérték-számításának gyakorlásához.

Függvények határértéke
-
Tananyag
Függvény jobb és bal oldali határértékéről tanulunk. Példákat oldunk meg jobb és bal oldali határértékre. Megnézzük, hogyan lehet a végtelen határérték. További függvények határértékét vizsgáljuk. Gyakorló feladatokat oldunk meg a függvények határérték számításával kapcsolatosan.

Még egy fontos függvény-típus
-
Tananyag
Függvények határértéke. Még egy újabb fontos függvény-típus határértékével foglalkozunk. Hogyan számoljuk ki a függvény hatérértékét, ha tört alakú, a nevezőben is és még a hatványkitevőben is szerepel az ismeretlen. Több feladatban gyakoroljuk.

Gyakorló feladatok
-
Tananyag
Ez a videó 14 függvény határérték számítás feladatot és azok megoldását tartalmazza. Először oldd meg a feladatokat, és csak utána nézd meg a megoldásokat!
Függvények deriválása
Csillagaim: 0 /12

Fogalmak, néhány függvény deriváltja
-
Tananyag
A differenciálszámítással az analízis egyik fontos mérföldkövéhez érkeztünk. Megtanuljuk mi a differenciahányados és differenciálhányados fogalma, mi a deriváltfüggvény. Meghatározzuk néhány függvény deriváltját: pl. sin x, cos x, ln x . Példákkal, feladatokkal gyakorlunk.

Deriválási szabályok
-
Tananyag
Differenciálási szabályokról, vagy más néven deriválási szabályokról lesz szó. Vajon hogyan hat a derivált értékére, ha a függvényekkel műveleteket végzünk: összeg- és különbségfüggvény, szorzat- és hányadosfüggvény deriváltját vizsgáljuk. Példákat, feladatokat oldunk meg a függvények deriválásának gyakorlására.

Összetett függvények deriválása
-
Tananyag
Az összetett függvényekkel foglalkozunk. Összetett függvények deriválását tanuljuk meg. Példákat,feladatokat oldunk meg az összetett függvény deriválásához. Többszörösen összetett függvények deriválására is sor kerül.

Gyakorló feladatok (deriválás)
-
Tananyag
Összefoglaljuk a deriválásról tanultakat. Elemi függvények deriváltjait és a deriválási szabályokat ismételjük át. Feladatokat oldunk meg a deriválás gyakorlásához.
Függvényvizsgálat

Függvényvizsgálat
-
Tananyag
Megtanuljuk, hogyan tudjuk felhasználni a differenciálszámítást a függvényvizsgálatnál: Mit árul el a derivált? Monoton növekvő vagy éppen csökkenő-e a függvény? Mely pontokban van a függvénynek lokális szélsőértéke? Konvex vagy konkáv a függvény? Mit nevezünk inflexiós pontnak?

Függvényjellemzés – ism. a középszintű anyagból
-
Tananyag
Meghatározzuk a függvény definícióját, az alaphalmazt és a képhalmazt, a zérushelyet, a szélsőértéket, a maximum- és minimum helyet (értéket). Megrajzoljuk a függvény grafikonját. A függvények tulajdonságaival foglalkozunk, ez a függvényjellemzés. Megvizsgáljuk, mi az értékkészlete, az értelmezési tartománya a függvénynek, csökkenő vagy növekvő a függvény.
Az integrálszámítás alapjai
Csillagaim: 0 /12

Integrálás, alapintegrálok
-
Tananyag
Az integrálást leegyszerűsítve a deriválás fordítottjának mondhatjuk. Beszélünk a határozatlan integrálról, más néven primitív függvényről. Sorra vesszük az integrálási szabályokat. Megvizsgáljuk az alapintegrálokat, majd néhány további függvény integrálját. Feladatok oldunk meg az integrálás gyakorlásához.

Integrálási módszerek 1.
-
Tananyag
Beavatunk a különböző integrálási módszerekbe. Összetett függvények deriváltját integráljuk. Megvizsgáljuk az alapintegrálokat. Példákat, feladatokat oldunk meg, integrálási típusok mutatunk be, és gyakoroljuk a számításokat.

Letölthető pdf file: Alapintegrálok
-
Tananyag
Töltsd le, és nyomtasd ki az alapintegrálokat!

Gyakorló feladatok a 2. videóhoz
-
Tananyag
Ebben a videóban 14 integrálszámítás feladatot és azok megoldásait találod. Először oldd meg a feladatokat, és csak azután nézd meg a megoldásukat!
Parciális integrálás és alkalmazások

Parciális integrálás
-
Tananyag
A parciális integrálás elvének megértéséhez a szorzatfüggvény deriváltjából indulunk ki. Példákat sorolunk és oldunk meg a parciális integrálásra. Exponenciális függvényeket, trigonometrikus függvényeket, logaritmus függvényeket, area és arkuszfüggvényeket integrálunk.
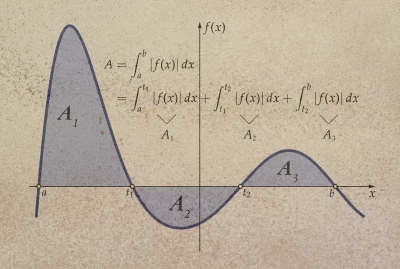
Határozott integrál és alkalmazásai
-
Tananyag
Határozott integrálról tanulunk. Megmutatjuk, hogyan tudjuk kiszámolni egy függvény-görbe alatti területét. Beavatunk a Newton – Leibniz tételbe. Példákat, feladatokat oldunk meg a határozott integrál számítás gyakorlására.
Analízis
6 alfejezet / 20 tananyag
01. Sorozatok határértéke
- Definíciók, alapok
Megvizsgáljuk a korlátos sorozatokat, az alsó-felső korlátot. Sorozatok monotonitásáról tanulunk: a szigorúan monoton csökkenő és növekvő sorozatokról. Megtanuljuk, mi a konvergencia, mitől konvergens a sorozat, és mit nevezünk a sorozat határértékének. Példákat, feladatokat oldunk meg sorozatokra.
A határérték számításhoz kapcsolódó tételek bizonyítására kerül sor ezen a videón: sorozatok összegére, különbségére, szorzatára, hányadosára vonatkozó tételek. Gyakoroljuk a határérték számítást példákkal, feladatokkal. Megvizsgáljuk a végtelenbe tartó sorozatokat. Ezek a valódi divergens sorozatok.
Nevezetes sorozatok határértékéről lesz szó. Megvizsgáljuk és bizonyítjuk a nevezetes sorozatok tételeit. Beszélünk a Bernoulli egyenlőtlenség, és megtudhatod azt is, mi az a rendőr elv (közrefogási elv). Példákkal, feladatokkal gyakorlunk.
Ebben a videóban olyan feladatokat gyűjtöttünk össze, melyek megoldásával gyakorolhatod a sorozatok határértékének kiszámítását. Sok szép feladat vár. Határozd meg a sorozatok határértékét!
02. Függvények határértéke, folytonossága
- Definíciók, alapok
Függvények határértékéről, függvények folytonosságáról tanulunk. Mikor folytonos és mikor nem folytonos egy függvény? Függvények összegének, különbségének, szorzatának, hányadosának határértékét vizsgáljuk. Példákat, feladatokat oldunk meg függvény határérték-számításának gyakorlásához.
Függvény jobb és bal oldali határértékéről tanulunk. Példákat oldunk meg jobb és bal oldali határértékre. Megnézzük, hogyan lehet a végtelen határérték. További függvények határértékét vizsgáljuk. Gyakorló feladatokat oldunk meg a függvények határérték számításával kapcsolatosan.
Függvények határértéke. Még egy újabb fontos függvény-típus határértékével foglalkozunk. Hogyan számoljuk ki a függvény hatérértékét, ha tört alakú, a nevezőben is és még a hatványkitevőben is szerepel az ismeretlen. Több feladatban gyakoroljuk.
Ez a videó 14 függvény határérték számítás feladatot és azok megoldását tartalmazza. Először oldd meg a feladatokat, és csak utána nézd meg a megoldásokat!
03. Függvények deriválása
- Fogalmak, néhány függvény deriváltja
A differenciálszámítással az analízis egyik fontos mérföldkövéhez érkeztünk. Megtanuljuk mi a differenciahányados és differenciálhányados fogalma, mi a deriváltfüggvény. Meghatározzuk néhány függvény deriváltját: pl. sin x, cos x, ln x . Példákkal, feladatokkal gyakorlunk.
Differenciálási szabályokról, vagy más néven deriválási szabályokról lesz szó. Vajon hogyan hat a derivált értékére, ha a függvényekkel műveleteket végzünk: összeg- és különbségfüggvény, szorzat- és hányadosfüggvény deriváltját vizsgáljuk. Példákat, feladatokat oldunk meg a függvények deriválásának gyakorlására.
Az összetett függvényekkel foglalkozunk. Összetett függvények deriválását tanuljuk meg. Példákat,feladatokat oldunk meg az összetett függvény deriválásához. Többszörösen összetett függvények deriválására is sor kerül.
Összefoglaljuk a deriválásról tanultakat. Elemi függvények deriváltjait és a deriválási szabályokat ismételjük át. Feladatokat oldunk meg a deriválás gyakorlásához.
04. Függvényvizsgálat
- Függvényvizsgálat
Megtanuljuk, hogyan tudjuk felhasználni a differenciálszámítást a függvényvizsgálatnál: Mit árul el a derivált? Monoton növekvő vagy éppen csökkenő-e a függvény? Mely pontokban van a függvénynek lokális szélsőértéke? Konvex vagy konkáv a függvény? Mit nevezünk inflexiós pontnak?
Meghatározzuk a függvény definícióját, az alaphalmazt és a képhalmazt, a zérushelyet, a szélsőértéket, a maximum- és minimum helyet (értéket). Megrajzoljuk a függvény grafikonját. A függvények tulajdonságaival foglalkozunk, ez a függvényjellemzés. Megvizsgáljuk, mi az értékkészlete, az értelmezési tartománya a függvénynek, csökkenő vagy növekvő a függvény.
05. Az integrálszámítás alapjai
- Integrálás, alapintegrálok
Az integrálást leegyszerűsítve a deriválás fordítottjának mondhatjuk. Beszélünk a határozatlan integrálról, más néven primitív függvényről. Sorra vesszük az integrálási szabályokat. Megvizsgáljuk az alapintegrálokat, majd néhány további függvény integrálját. Feladatok oldunk meg az integrálás gyakorlásához.
Beavatunk a különböző integrálási módszerekbe. Összetett függvények deriváltját integráljuk. Megvizsgáljuk az alapintegrálokat. Példákat, feladatokat oldunk meg, integrálási típusok mutatunk be, és gyakoroljuk a számításokat.
Töltsd le, és nyomtasd ki az alapintegrálokat!
Ebben a videóban 14 integrálszámítás feladatot és azok megoldásait találod. Először oldd meg a feladatokat, és csak azután nézd meg a megoldásukat!
06. Parciális integrálás és alkalmazások
- Parciális integrálás
A parciális integrálás elvének megértéséhez a szorzatfüggvény deriváltjából indulunk ki. Példákat sorolunk és oldunk meg a parciális integrálásra. Exponenciális függvényeket, trigonometrikus függvényeket, logaritmus függvényeket, area és arkuszfüggvényeket integrálunk.
Határozott integrálról tanulunk. Megmutatjuk, hogyan tudjuk kiszámolni egy függvény-görbe alatti területét. Beavatunk a Newton – Leibniz tételbe. Példákat, feladatokat oldunk meg a határozott integrál számítás gyakorlására.
Évvégi ismétlő/ próba pótvizsga feladatsorok
Ismétlés
Csillagaim: 0 /18

1. feladatsor
-
Tananyag
Hat feladat (megoldások nélkül) a 11. osztályos matematika tananyagból, melyek megoldásával ellenőrizheted, illetve próbára teheted a tudásod. Koordinátageometriai feladatok (szinusz-, koszinusz – tétel, egyenes egyenlete), exponenciális-, logaritmikus-, trigonometrikus egyenletek várnak. Útmutatást, jó tanácsokat is adunk ebben a videóban.

1. feladatsor megoldásai
-
Tananyag
Az előző videó feladatinak megoldását találod itt. Koordinátageometriai feladatok (szinusz-, koszinusz – tétel, egyenes egyenlete), exponenciális-, logaritmikus-, trigonometrikus egyenletek megoldása vár. Ellenőrizheted magad, és el is magyarázzuk a helyes megoldást.

2. feladatsor
-
Tananyag
Újabb hat feladat (megoldások nélkül) a 11. osztályos tananyagból. Ezek megoldásával kiderítheted, vannak-e hiányosságaid, illetve még jobban rögzítheted mindazt, amit tudsz. Exponenciális függvény ábrázolása, exponenciális-, logaritmikus-, trigonometrikus egyenletek, paralelogramma oldalainak kiszámítása vár, valamint egy koordinátageometriai feladat: Kör és az érintő egyenletének felírása.

2. feladatsor megoldásai
-
Tananyag
Az előző videó feladatainak megoldásait találod itt. Exponenciális függvény ábrázolása, exponenciális-, logaritmikus-, trigonometrikus egyenletek, paralelogramma oldalainak kiszámításának megoldása vár, valamint egy koordinátageometriai feladat: Kör és az érintő egyenlete.

3. feladatsor
-
Tananyag
Ezt a videót a legnehezebb témakörök gyakorlására tettük be az érettségi tréning videói közé. A 11.-es matekban ez év végi ismétlő feladatsorként ill. próba-pótvizsga feladatsorként szerepel. A példák között szerepel két logaritmusos és egy exponenciális egyenlet, egy trigonometrikus egyenlet, egy geometria példa szinusz,-és koszinusz-tétel gyakorlására, valamint két koordinátageometria feladat. A megoldásokat a következő videón láthatod.

3. feladatsor megoldásai
-
Tananyag
Az előző videó feladatainak megoldása vár. Ellenőrizheted magad, és el is magyarázzuk a helyes megoldást. Trigonometrikus-, exponenciális-, logaritmikus egyenleteket kellett megoldanod. Mekkora a háromszög legnagyobb szöge? Koordinátageometriai feladat: Írd fel a P és Q ponton átmenő egyenes egyenletét! Milyen messze van a kör középpontja az origótól?
Évvégi ismétlő/ próba pótvizsga feladatsorok
1 alfejezet / 6 tananyag
01. Ismétlés
Hat feladat (megoldások nélkül) a 11. osztályos matematika tananyagból, melyek megoldásával ellenőrizheted, illetve próbára teheted a tudásod. Koordinátageometriai feladatok (szinusz-, koszinusz – tétel, egyenes egyenlete), exponenciális-, logaritmikus-, trigonometrikus egyenletek várnak. Útmutatást, jó tanácsokat is adunk ebben a videóban.
Az előző videó feladatinak megoldását találod itt. Koordinátageometriai feladatok (szinusz-, koszinusz – tétel, egyenes egyenlete), exponenciális-, logaritmikus-, trigonometrikus egyenletek megoldása vár. Ellenőrizheted magad, és el is magyarázzuk a helyes megoldást.
Újabb hat feladat (megoldások nélkül) a 11. osztályos tananyagból. Ezek megoldásával kiderítheted, vannak-e hiányosságaid, illetve még jobban rögzítheted mindazt, amit tudsz. Exponenciális függvény ábrázolása, exponenciális-, logaritmikus-, trigonometrikus egyenletek, paralelogramma oldalainak kiszámítása vár, valamint egy koordinátageometriai feladat: Kör és az érintő egyenletének felírása.
Az előző videó feladatainak megoldásait találod itt. Exponenciális függvény ábrázolása, exponenciális-, logaritmikus-, trigonometrikus egyenletek, paralelogramma oldalainak kiszámításának megoldása vár, valamint egy koordinátageometriai feladat: Kör és az érintő egyenlete.
Ezt a videót a legnehezebb témakörök gyakorlására tettük be az érettségi tréning videói közé. A 11.-es matekban ez év végi ismétlő feladatsorként ill. próba-pótvizsga feladatsorként szerepel. A példák között szerepel két logaritmusos és egy exponenciális egyenlet, egy trigonometrikus egyenlet, egy geometria példa szinusz,-és koszinusz-tétel gyakorlására, valamint két koordinátageometria feladat. A megoldásokat a következő videón láthatod.
Az előző videó feladatainak megoldása vár. Ellenőrizheted magad, és el is magyarázzuk a helyes megoldást. Trigonometrikus-, exponenciális-, logaritmikus egyenleteket kellett megoldanod. Mekkora a háromszög legnagyobb szöge? Koordinátageometriai feladat: Írd fel a P és Q ponton átmenő egyenes egyenletét! Milyen messze van a kör középpontja az origótól?

A legnehezebb matek-anyagokkal kell megbirkóznod 11. osztályban. Logaritmus, szinusz-koszinusz, és még a koordinátageometria is ebbe az évbe van belesűrítve.
Ha dolgozatra készülsz, jobb segítséget nem is találhatnál: egy-egy témakört rendkívül gyorsan és eredményesen tudsz átismételni úgy, hogy közben “bemászik a fejedbe” a matektudás.
Egyszerű, érthető, vidám matek 🙂 Erőlködés és görcsök nélkül tanulhatod a matekot, és végre mindent érteni fogsz! Mindezt úgy, hogy még unalmas sem lesz a matektanulás. Világosan elmagyarázunk mindent, közben már gyakorolhatsz is, és folyamatosan ellenőrizheted magad. Próbáld ki! B. Békési Bea
A szerethető matektanulás szakértője
Matektanár

Nagyon sokat köszönhetek a matekmindenkinek.hu oldal szerkesztőinek! 11-es vagyok és ugye ez már az egyetemi felvételinél beleszámít. Az utolsó 2 dolgozatomat sikerült négyesre megírnom (2 témazáró), ezért év végén is remélhetőleg meg lesz a négyes. A videók nagyon igényesen vannak összeállítva többféle szempontból is, könnyen kezelhetőek, remek gyakorlási lehetőséget biztosítanak 1-1 dolgozat előtt. Szóval köszönöm szépen a segítséget! 😉

Soha nem gondoltam volna, hogy a matekot élvezni is lehet. Nagyon jó eredményeket értem el, mióta használom az oktató csomagot, ráadásul a fiam, aki szintén 11. osztályos, de ő természetesen nappalin jár, ő is sokkal jobb jegyeket hoz matekból, amióta velem együtt készül az órákra. Egyszóval: fantasztikus!
Comments are closed, but trackbacks and pingbacks are open.