Itt van a középszintű magyar írásbeli érettségi feladatsora és a javítási útmutató

Arany János Őszikék ciklusa. 3. Ady Endre Léda-verseinek tartalmi és . A magyar nyelv történetének fő korszakai. 6. A nyelvtörténet forrásai: kézírásos és .

Tényleg túl nehéz volt?

A matematika érettségi vizsga is kicsit olyan, mint a magyar foci: mindenki ért hozzá, de legalábbis véleménye van róla. Általában lesújtó. A vizsga délutánjától kezdve a különböző internetes fórumokat ellepik a hozzászólások, amelyek egy részéből, ha a csúnya szavakat kihagynánk, csak a kötőszavak és az írásjelek maradnának. Mindenekelőtt természetesen az idei volt a legnehezebb . Minden évben. A hozzászóló az összes eddigi feladatsort megoldotta, de az idei feladatokhoz még csak hasonlókkal sem találkozott . Mert több feladat egyértelműen emelt szintű volt – a középszintű feladatsorban .

Mindig vannak persze józanabb hangok is. Érdekes, hogy a kétféle típusú komment arányából elég nagy pontossággal meg lehet jósolni már a vizsga napján a végső országos átlagot. Mert ha igaz is, hogy nincs internetes fórum szélsőséges hozzászólások nélkül, azért az érettségiző közvélemény összességében mégis egy elég érzékeny barométer, amelyik általában pontosan visszatükrözi azt, ha egy feladatsor 2-3%-kal könnyebbre vagy nehezebbre sikerült a korábbi sokéves átlagnál.[1]

A 2019-es év ebből a szempontból különleges volt. Már a vizsga napján egy online petíció indult „Vigyék lejjebb a ponthatárt a 2019-es májusi matematika érettségin az irreálisan nehéz feladatok miatt” címmel, amit fél nap alatt több mint 28 ezren írtak alá (természetesen messze nem mind érettségizők). A hírportálokat ellepték a vizsga nehézségét reklamáló visszhangokról szóló tudósítások. Az első vizsgahét szombatjára pedig tüntetést hirdettek az Oktatási Hivatal elé, amelyre az egyik közösségi oldalon több mint 5000-en jelezték részvételüket. A petíciót aláírók száma végül valamivel 33 ezer fölött állt meg, a meghirdetett tüntetés viszont látványos érdektelenségbe fulladt, összesen 2-3 tucat érdeklődő vett rajta részt. De a hullámverés már akkora volt, hogy az Oktatási Hivatalnak is reagálnia kellett. Ekkor azonban még senki nem tudta biztosan megmondani, hogy vajon tényleg nehéz, esetleg túl nehéz volt-e a feladatsor.

Talán kevesen tudják, de a kétszintű rendszerben keletkezett összes vizsgaeredmény (természetesen név és iskolanév nélkül) nyilvános. A május-júniusi vizsgák eredményei általában július második felétől érhetőek el az interneten. Azonban már ennél korábban is viszonylag megbízható információk állnak rendelkezésre a májusban írt magyar nyelvű[2] matematika feladatsorok eredményességéről, ráadásul olyan részletességgel, amellyel az említett honlap nem szolgál.

A kétszintű érettségi szoftverben a matematika vizsgadolgozatokról az I. és a II. rész pontszámán kívül további részleteket nem kell rögzíteni, így a feladatonkénti pontszámok országos eloszlásáról korábban nem álltak rendelkezésre adatok. Ezen a helyzeten próbált változtatni az érettségi tételkészítő bizottság, amikor először a 2012-es májusi-júniusi vizsgaidőszakban (az Oktatási Hivatal támogatásával és közreműködésével, az Adafor rendszeren keresztül) az iskolákat önkéntes adatszolgáltatásra kértük: küldjék el a náluk jelentkező vizsgázók pontszámát feladatonkénti részletezéssel. Idén pedig már nyolcadszor végeztük el ezt a kutatást.

A nyolc év alatt tekintélyes mennyiségű adat gyűlt össze: összesen kb. 200 ezer középszintű vizsgázó által megoldott összesen 144 feladat, valamint kb. 7 ezer emelt szintű vizsgázó által megoldott összesen 72 feladat pontszámának részletes adataival rendelkezünk. 2018-ban tovább bővítettük a kutatást: arra kértük az együttműködő iskolákat, hogy ha idejük engedi, akkor ne feladatonként, hanem alfeladatonként rögzítsék a vizsgázók pontszámait. Amennyiben erre nem tudtak vállalkozni, úgy továbbra is elfogadtuk a feladatonként rögzített pontszámokat.

A több éves tapasztalat szerint jellemzően a vizsgázók 25-35%-áról kapunk adatokat. Bár a beérkezett adatok az összes vizsgázóra nézve szigorú értelemben nem tekinthetők reprezentatívnak, az bizonyos, hogy a minta nagysága lehetővé teszi a teljes vizsgázói populációra vonatkozó megalapozott következtetések levonását. Az adatok pedig már június végén rendelkezésre állnak, így tehát akkortájt lényegében már biztosat lehet tudni az aktuális év magyar nyelvű feladatsorainak megoldottságáról.

Az összegyűlt adatokból levonható tanulságok fontosságát nem lehet eléggé hangsúlyozni. Az írásbeli matematikaérettségi tartalmi és formai követelményeit a részletes érettségi vizsgakövetelmények és a vizsgaleírás szabályozzák. Ebből a szabályozásból azonban nem vezethető le (legfeljebb viszonylag tág határok között) az, hogy milyen nehéznek kell lennie összességében egy feladatsornak. Ezt egyfajta közmegegyezés vagy szokásjog szabályozza: legyen nagyjából olyan nehéz, mint a sokéves átlag – ez felel meg az igazságosság követelményének is, hiszen a felsőoktatási felvételi eljárás során a különböző években (különböző feladatsorokon) érettségizett jelentkezők is versenyeznek egymással. Természetes elvárás tehát, hogy az egyes feladatsorok megoldottságának terjedelme és szórása egy elfogadható határon belül maradjon. Hogy mi tekinthető elfogadhatónak, az megint nincs sehol leírva, de valószínűleg nem tévedünk nagyot, ha azt mondjuk, hogy jogos kívánalom, hogy a megoldottság sokéves távlatban egy kb. 5-6% szélességű intervallumon belül mozogjon.

Ezt az elvárást a májusi magyar nyelvű középszintű feladatsorok, ha nem is tökéletesen, de elfogadhatóan teljesítik (1. ábra). A 2007 és 2019 között megírt 13 feladatsor közül csak kettőnek a megoldottsága nem esik bele a [44,4%; 50,4%] intervallumba (2007: 42,7%, 2015: 42,9%), de ezeket figyelembe véve is a 13 adat terjedelme 8% alatt marad, az adatok szórása pedig 2,4%. Emelt szinten kicsit rosszabb a helyzet: négy feladatsor megoldottsága nem esik bele a [64,2%; 70,2%] intervallumba. Ezek közül kettő épphogy, de lefelé lóg ki (2016: 62,4%, 2017: 63,0%), kettő viszont – egymással ellentétes irányban – erőteljesen (2007: 78,1%. 2013: 55,2%), az adatok szórása pedig 3,0% (2. ábra). A 2013-as feladatsor védelmére számos érvet fel lehet hozni, de biztosan senki nem kívánja az eredményességének a megismétlődését.

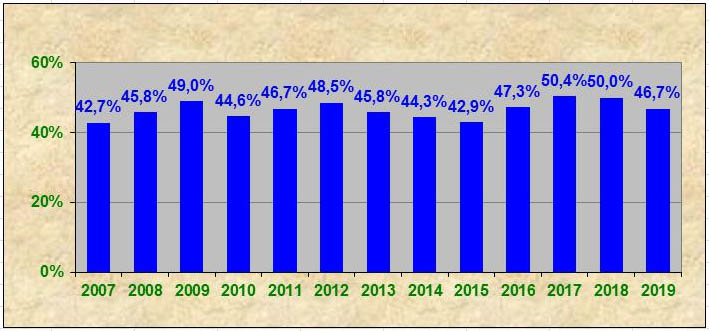
1. ábra: A májusi magyar nyelvű középszintű írásbeli feladatsorok megoldottsága (2007-2019)

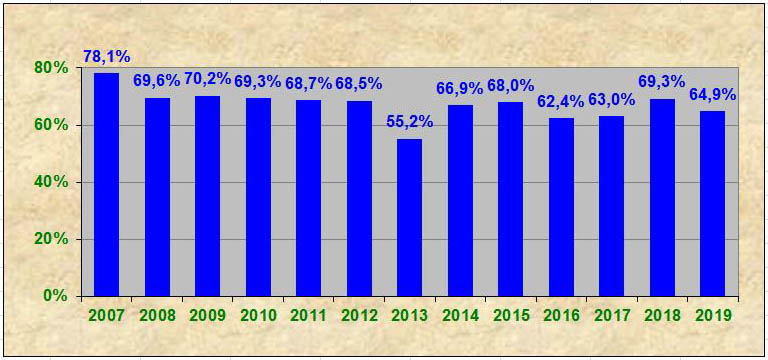
2. ábra: A májusi magyar nyelvű emelt szintű írásbeli feladatsorok megoldottsága (2007-2019)

Adódik a kérdés, hogy egy feladatsor elkészítésekor hogyan lehetséges annak későbbi eredményességét egy 6%-os szélességű intervallumba pozícionálni? Mivel a magyar érettségi rendszerben az érettségi feladatok, feladatsorok kipróbálására semmilyen mód nincs, erre garanciát adni biztosan nem lehet, tehát inkább arról a kívánalomról beszélhetünk, hogy a lehető legnagyobb valószínűséggel érjük el ezt a célt. Ennek biztosítéka egyedül a feladatkészítés folyamata, a több körös lektorálás, és a folyamatban részt vevők szakmai tapasztalata lehet. A feladatonkénti (és most már alfeladatonkénti) eredményesség vizsgálata azt jelenti, hogy a közreműködő szakemberek nem csak a tapasztalataikra és intuíciójukra, hanem immár egy egyre bővülő adatsorra is támaszkodhatnak, amikor egy-egy feladat, feladatsor várható eredményességét a kívánt szintre igyekeznek beállítani. Mai tudásunkkal, nyolc év adatainak birtokában már pontosan rá tudunk mutatni azokra a jellemzőkre is, amelyek a 2013-as emelt szintű feladatsor kívánatosnál alacsonyabb megoldottságát okozták. De ezek az információk akkor még nem álltak rendelkezésünkre.

Bár az idei feladatsort elkészítők és lektorálók körében (a tiltakozásokról szóló híreket olvasva is) általános volt a meggyőződés, hogy az valójában nem lehetett nehezebb (sőt inkább könnyebb volt) a sokéves átlagnál, azért mégis mindenki a szokásosnál nagyobb izgalommal várta, hogy a beérkező adatok ezt a véleményt vajon visszaigazolják-e? Vagy pedig a megszokottnál jóval nagyobb zúgolódás valóban azt jelenti, hogy (várakozásaink ellenére) nem sikerült jól eltalálni a feladatsor nehézségét, és az az átlagnál (és a kívánatosnál) jóval nehezebbre sikerült? Ha igen, vajon miért? Ha nem, akkor mi okozhatta a máskor nem tapasztalt felháborodási hullámot? Az a kritika ugyan biztosan nem volt megalapozott, hogy betű szerint ne felelt volna meg a feladatsor a középszintű követelményeknek, de mint mondtuk, a jogszabályokból nem vezethető le az összesített nehézségre vonatkozó precíz előírás. Így egy 35%-os és egy 60%-os eredményességű feladatsor is képes lehet tökéletesen megfelelni a szabály betűjének, de az bizonyos, hogy az előbbiből valóban méretes országos botrány lenne (nem ok nélkül), és az utóbbi sem lenne szerencsés.

Az eredmény ma már ismert: ennél átlagosabb nem is lehetett volna egy feladatsor. A megelőző 12 májusi magyar nyelvű feladatsor átlagos megoldottsága 46,5% volt, az idei feladatsoré 46,7%.[3] Tény, hogy 2007 óta kivétel nélkül minden évben a középszintű matematika eredmények lettek a leggyengébbek a tíz „nagy” vizsgatárgy[4] közül. Általában nem is kevéssel. Külön tanulmányt érne meg annak a vizsgálata, hogy ez miért van így. De az is tény, vagy legalábbis a matematikatanárok körében biztos meggyőződés, hogy annál kevesebb matematikatudásra nem nagyon értelmezhető érettségi bizonyítványt adni, mint ami jelenleg az elégségeshez szükséges (és elégséges). Persze az a kérdés is felvethető (de szintén messzire vezetne), hogy biztosan kell-e valakinek matematikából sikeresen érettségizni ahhoz, hogy érettségi bizonyítványt kapjon. A magyar jogszabályok szerint (néhány ritka, speciális felmentés kivételével) igen, és ez mindig is így volt, de az egyes országok gyakorlata ebben eltérő.

De miért is volt akkor a nagy felzúdulás? Erre természetesen nincs egzakt válasz, csak feltételezéseink lehetnek. Az első ok mindjárt egy szinte véletlen hatás: a Frankfurter Allgemeine Zeitung egy nappal a magyar vizsga előtt írt arról, hogy túl nehéz volt Németországban az idei matematikaérettségi, ezért a diákok online petíciót indítottak. A cikket másnap, tehát éppen a magyar matematikaérettségi napján hazai hírportálok is idézték. Nem kellett tehát túl nagy fantázia, de még egy túl nehéz feladatsor sem ahhoz, hogy valaki a német példán fellelkesülve a magyar feladatsort kifogásoló petíciót indítson.

Már említettük a matematika vizsgaeredmények többi vizsgatárgyhoz viszonyított gyengeségét. Így tehát az is tény, hogy minden évben tízezrével vannak olyanok, akik a matematikaérettségit (annak aktuális nehézségétől függetlenül) tényleg nagyon nehéznek találják, és legfeljebb az elégségesért küzdenek.[5] Az ő körükben bizonyára jó talajra hullott a felhívás, és sokan találva érezték magukat, így ők, valamint barátaik és rokonaik is készségesen aláírták a petíciót.

Végül pedig az is tény, hogy miközben az idei feladatsor „teljesítette” a 12 éves átlagot, de eredményessége kb. 3,5 százalékponttal elmaradt a megelőző két év feladatsorainak megoldottságától (melyek viszont a 12 év két legmagasabb átlagát hozták), így sokakban valóban lehetett egy olyan érzés, hogy „ez nehezebb, mint a szokásos”. (És mivel nem ideillő, arról nem beszélünk részletesen, hogy vannak, akik bármi ellen szívesen tiltakoznak, ha mód van rá. Különösen, ha oktatásról van szó.)

Amikor pedig az érettségi eredmények országos összesítéséről az Oktatási Hivatal július második felében hírt ad (például itt vagy itt), az már természetesen messze nem kelt akkora csatazajt, mint a májusi tiltakozások híre, és jó esetben egy-egy rövid közleményt érdemel ki azokon a hírportálokon, melyek bőséges terjedelemben számoltak be korábban a petícióról és a tüntetésről.

A feladatsor nehézségét kritizálók leggyakrabban azt kifogásolták, hogy a feladatsor II.B része[6] három, egyaránt nagyon hosszú szövegű feladatot tartalmazott: „Sokáig tart őket végigolvasni, és így megtudni egyáltalán azt, melyik milyen témakörhöz kapcsolódik” – olvashattuk például egy matematikatanár mértéktartónak számító véleményét. Az internetes fórumokon sokan ennél jóval durvábban fogalmaztak.

Ma már bőségesen elegendő adat áll rendelkezésünkre ahhoz, hogy számos, intuitív módon megfogalmazott állítás igazságát statisztikailag alátámasszuk vagy megcáfoljuk. Ezt most meg is tesszük három, széles körben hangoztatott kijelentés esetében:

1. Az idei középszintű matematikaérettségi feladatainak szövege hosszú volt.

2. A hosszú feladatsorok és a hosszú szövegű feladatok általában nehezebbek, mint a rövidebbek.

3. A hosszú szövegű feladatokat nem szeretik a vizsgázók, szívesen kihagyják ezeket, ha tehetik.

1. Az idei középszintű matematikaérettségi feladatainak szövege hosszú volt.

Egy feladatsor „hosszát” a feladatok szövegének összesített karakterszámával mérjük (és eltekintünk az esetleges kiegészítő ábráktól, mert azok hosszát nem tudjuk értelmezni). Itt most csak a II. rész hosszát vizsgáljuk. Az I. rész hossza egyrészt nem mutat jelentős ingadozást, másrészt lényegében kizárható, hogy összességében 2-300 karakternyi eltérés érdemben befolyásolná a megoldottságot.

A II. rész hosszát tekintve valóban tetten érhető egy növekvő tendencia. A 2007 óta kitűzött 13 feladatsor közül az öt leghosszabb az elmúlt hat évben szerepelt. És tény, hogy az idei feladatsor volt az eddigi leghosszabb a maga 5188 karakterével.

Érdemes azért hangsúlyozni, hogy nincs arról szó, hogy a feladatsorok hossza vagy jellege folyamatos változásban lenne, így a vizsgázók sosem tudhatnák biztosan, hogy mire készülhetnek. Inkább az a helyzet, hogy a kétszintű rendszer életbelépésével (2006) radikálisan megváltozott matematikavizsgának is kellett néhány év, ami alatt a szerkezet és stílus kikristályosodása, finomhangolása megtörtént. Míg a kétszintű rendszerben kitűzött első feladatsorok óta valóban tetten érhető néhány kisebb változás (ld. például itt), az elmúlt néhány évben megszületett feladatsorok már állandóságot mutatnak, és a változások jogszabályban megragadható részét a vizsgaleírás 2017-től életbe lépő változásában kodifikálták is.

2. A hosszú feladatsorok és a hosszú szövegű feladatok általában nehezebbek, mint a rövidebbek.

Ez a mondat két állítást tartalmaz, amelyeket külön fogunk vizsgálni. Koncentráljunk először a feladatsorok összesített hosszára. Mutat-e ez összefüggést az adott feladatsor megoldottságával? A korrelációs együtthatót hívjuk segítségül.[7] Figyelembe kell venni, hogy az adatok viszonylag alacsony száma miatt (13 év 13 feladatsora) csak óvatos következtetéseket lehet megfogalmazni, továbbá egy-egy kiugró adat ilyen kis elemszámnál jelentősen torzítani tudja a kapott eredményt.

Mindezeket előrebocsátva a 2007 és 2019 közötti májusi középszintű feladatsorok II. részének karakterszámban mért hosszúsága és megoldottsága közötti korrelációs együttható –0,30-nak adódik. Ez egy nem túl erős, de már érezhető összefüggést jelent, amit a 3. ábra is megerősít. A negatív korrelációs együttható fordított összefüggésre utal (tehát a hosszabb feladatsor megoldottsága jellemzően alacsonyabb), ezért az ábrán a jobb oldali tengelyen a megoldottsági skálát fordítva helyeztük el, annak kezdő és végpontját úgy megválasztva, hogy az összefüggés minél jobban látható lehessen. A bevezetőben utaltunk arra, hogy a kevés adat miatt az érték nem alkalmas messzemenő következtetések levonására; ezt alátámasztja, hogy ha a II. rész idei eredményessége mindössze 9 százalékponttal jobb lett volna a ténylegesnél, akkor a 13 adatpár korrelációs együtthatója egyenesen pozitívba fordult volna.

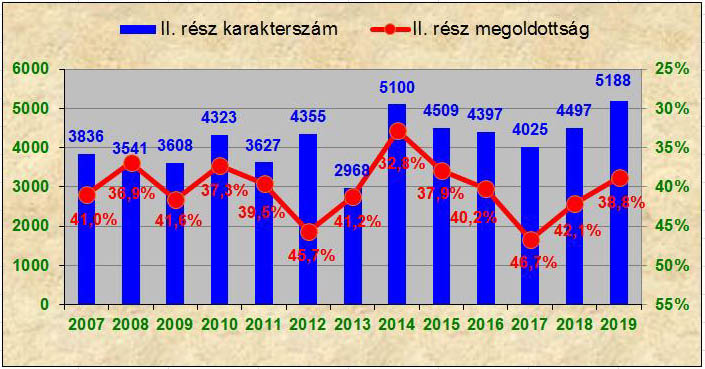
3. ábra: A májusi magyar nyelvű középszintű írásbeli feladatsorok II. részének
karakterszámban mért hosszúsága és megoldottsága (2007-2019)

Érdekes, hogy az októberi feladatsorok tekintetében ugyanez az érték –0,70, ami már erősebb összefüggésre utal. Ennek több oka lehet. A legfontosabb talán az, hogy októberben egy jóval gyengébb mezőny vizsgázik (2018-ban az októberi vizsgák közel 43%-a javítóvizsga volt), és a vizsgázók egy nem elhanyagolható részének a szövegértés is komoly nehézséget okoz, így ők a májusban érettségizőkhöz képest jóval érzékenyebbek a feladatsor hosszának ingadozására. Egy másik lényeges tényező pedig az lehet, hogy a feladatsorok hosszának lassú, mégis tendenciaszerű növekedése egybeesett a vizsgaszabályzat változásával, melynek értelmében 2014-től kezdve ősszel nem lehetett előrehozott vizsgát tenni, így az októberben vizsgázókon belül tovább nőtt a javítóvizsgázók aránya.

Végül megemlítjük, hogy a májusi magyar nyelvű emelt szintű feladatsorok esetében a korrelációs együttható értéke –0,40, ami egy létező, gyenge-közepes összefüggésre utal.

Vizsgáljuk meg most az állítás második részét, tehát az egyes feladatok szövegének hosszúságára vonatkozó kijelentést. 2012 óta valamennyi májusban kitűzött feladat megoldottságáról megbízható adataink vannak[8], a feladatok szövegének hosszát pedig ugyanúgy a szöveg karakterszámával mérjük.

A korrelációs együtthatókat kiszámítva kijelenthető, hogy gyakorlatilag kimutathatatlan bármilyen összefüggés egy feladat szövegének hosszúsága és a feladat megoldottsága között. A 2012 és 2019 között a középszint II. részében kitűzött 48 feladat esetén a korrelációs együttható –0,13. Ezt a pontdiagram (4. ábra) is megerősíti, amelyen egy negatív meredekségű egyenes körüli sűrűsödést kellene látnunk, ha a vélt összefüggés létezne.

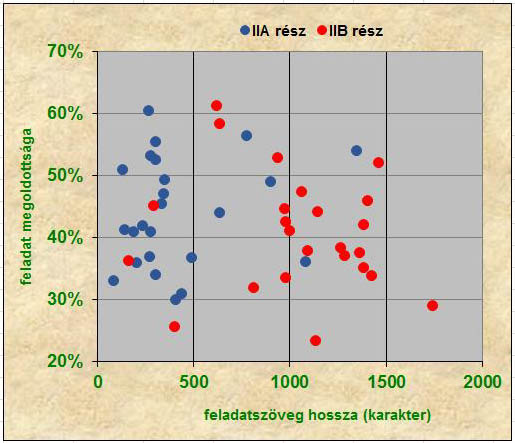
4. ábra: A májusi magyar nyelvű középszintű írásbeli feladatsor II. részében kitűzött feladatainak
karakterszámban mért hosszúsága és megoldottsága (2007-2019)

Az emelt szinten a vizsgált időszakban kitűzött 72 feladat esetén a korrelációs együttható –0,19, amely egy kicsivel több a középszintűnél, és valahol a határán lehet annak, hogy egy igen gyenge összefüggésről beszélhessünk (5. ábra). De ez a kép csalóka: a –0,19-es érték szinte kizárólag abból adódik, hogy a II. rész feladatai (5−9.) a vizsgaleírásból adódóan hosszabbak, összetettebbek és nehezebbek, így a vizsgázók azokon kevésbé eredményesek, mint az I. rész feladatain (1−4.). Ezt bizonyítja, hogy ha „a körtét a körtével” hasonlítjuk össze, és külön-külön kiszámítjuk a korrelációs együtthatót az I., illetve a II. részben, akkor mindkét esetben mindössze –0,03-at kapunk.

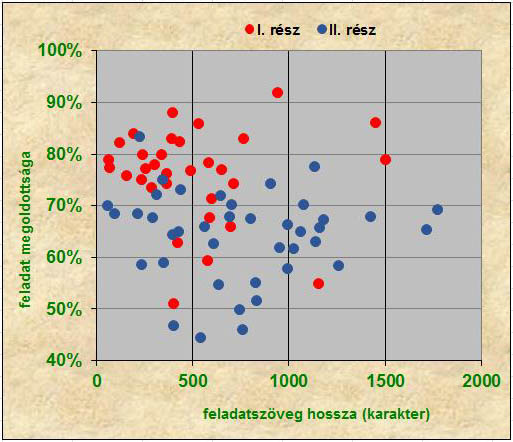
5. ábra: A májusi magyar nyelvű emelt szintű írásbeli feladatsorokban kitűzött feladatok
karakterszámban mért hosszúsága és megoldottsága (2007-2019)

Ha ezen felbátorodva középszinten is külön megvizsgáljuk a II.A, illetve a II.B részt, akkor azt tapasztaljuk, hogy az A résznél egyenesen pozitív a korreláció (0,18), tehát itt éppenséggel kicsivel még jobban is sikerülnek a valamivel hosszabb szövegű feladatok. Valóban lehetnek olyan rövid szövegű feladatok, ahol az a helyzet, hogy a vizsgázó vagy tudja a megoldást vagy pedig egyáltalán nem tudja, és nehezebb elképzelni az átmeneti állapotot. Egy hosszabb szöveg esetén viszont több olyan fogódzó lehet, amiből ha teljes megoldásra nem is jut el egy vizsgázó, de részpontszámokat könnyebb szereznie. Külön csak a B részre vonatkozó korrelációs együttható –0,16.

3. A hosszú szövegű feladatokat nem szeretik a vizsgázók, szívesen kihagyják ezeket, ha tehetik.

A feladat hosszának szövege és a feladatot kihagyó vizsgázók aránya közötti korrelációs együttható középszinten –0,05, emelt szinten +0,04. Egyik esetben sem mutatható ki semmilyen összefüggés (6. és 7. ábra).

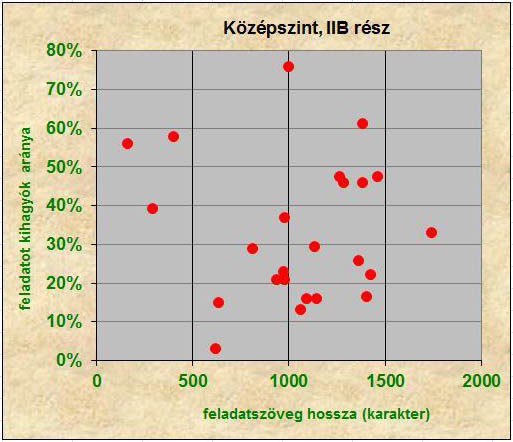
6. ábra: A májusi magyar nyelvű középszintű írásbeli feladatsorok II.B részében kitűzött feladatok
karakterszámban mért hosszúsága és a feladatokat kihagyók aránya (2007-2019)

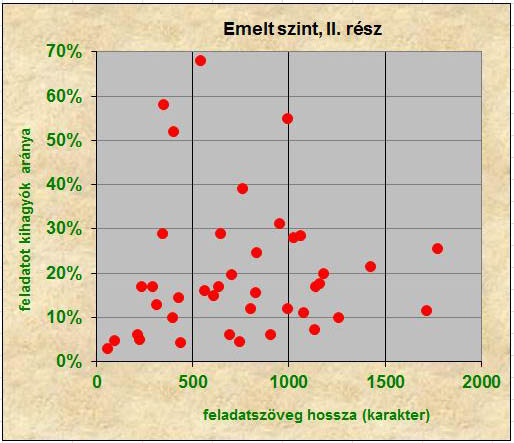
7. ábra: A májusi magyar nyelvű emelt szintű írásbeli feladatsorok II. részében kitűzött feladatok
karakterszámban mért hosszúsága és a feladatokat kihagyók aránya (2007-2019)

Az alaposabb vizsgálat tehát nem támasztja alá (sőt lényegében cáfolja) azt a (viszonylag széles körben elterjedt) vélekedést, hogy egy feladat általában nehezebb, ha hosszú a szövege; sem pedig azt, hogy a vizsgázók a hosszabb szövegű feladatokat szívesebben hagyják ki. Míg azonban feladatonként vizsgálva nem igazolódott az, hogy a hosszabb a nehezebb, egy teljes feladatsort tekintve annyit mondhatunk, hogy a hosszabbak valamivel nagyobb valószínűséggel bizonyulnak nehezebbnek. Az összefüggés azonban gyenge, mert egy feladatsor nehézségét sok más tényező is (a hosszúságnál meghatározóbb módon) befolyásolja.

Bár a matematikaérettséginek csak néhány aspektusát érintettük, az talán az eddigiekből is kiderült, hogy az iskolák által küldött feladatonkénti visszajelzések jelentősége óriási. Itt is biztatunk ezért minden matematika munkaközösséget, hogy (az Adafor rendszeren keresztül az írásbeli vizsga után érkező kérésnek megfelelően) küldjék el az Oktatási Hivatalnak az iskolában érettségizők részletes pontszámait. „Cserébe” a visszajelzések alapján évről évre készülő elemzést (szintén Adaforon keresztül) szeptemberben kapják meg az iskolák. Az elmúlt nyolc év adatszolgáltatásához nyújtott segítséget és fáradozást pedig köszönjük!

Csapodi Csaba mesteroktató,

ELTE TTK Matematikai Intézet, Matematikatanítási és Módszertani Központ

az Óbudai Árpád Gimnázium igazgatóhelyettese, a tételkészítő bizottság elnöke

A cikk a 2019. évi Rátz László Vándorgyűlésen elhangzott előadás anyagának felhasználásával készült.

Megjelent a médiában:

Elemzések, tanulmányok a matematikaérettségiről:

Csaba Csapodi and Levente Koncz: The efficiency of written final exam questions in mathematics based on voluntary data reports, 2012–2015
Teaching Mathematics and Computer Science, 2016/14 p63-81):
http://tmcs.math.unideb.hu/load_doc.php?p=306&t=abs

A matematika érettségi vizsga elemzése 2005-2015 (Csapodi Csaba doktori értekezése):
https://dea.lib.unideb.hu/dea/handle/2437/236563

[1] A cikkben végig azzal az előfeltevéssel élünk, hogy az egymást követő érettségiző évfolyamok átlagos matematikatudása lényegében megegyezik, ezért az egyes feladatsorok megoldottságának ingadozása és az ingadozás mértéke a feladatsorok változó nehézségének a következménye.

[2] A május-júniusi vizsgaidőszakban a magyar nyelven vizsgázók, illetve (jellemzően a két tanítási nyelvű intézményekben) idegen nyelven vizsgázók (biztonsági okokból) két különböző feladatsort oldanak meg.

[3] A matematika érettségi eredmények átlaga ennél magasabb (2019-ben 48,9%), mert a szóbeli vizsgák és az idegen nyelven vizsgázók eredményei is javítják az átlagot.

[4] matematika, magyar nyelv és irodalom, történelem, angol nyelv, német nyelv, biológia, fizika, kémia, informatika, földrajz

[5] Az elmúlt öt év átlagában a május-júniusi vizsgaidőszakban matematikából legfeljebb elégségesre vizsgázók aránya 41%.

[6] A vizsgaleírás szerint: „A II.B rész három, egyenként 17 pontos feladatot tartalmaz, amelyből a vizsgázó választása szerint kettőt kell megoldani, és csak ez a kettő értékelhető. A feladatok a középszintű követelmények keretein belül összetett feladatok, általában több témakört is érintenek és több részkérdésből állnak.”

[7] Két adatsor közötti korrelációs együttható egy –1 és +1 közötti szám. A szám előjele a kapcsolat irányát, abszolútértéke pedig a kapcsolat szorosságát jellemzi. Ha az együttható nulla, akkor a két adatsor teljesen független egymástól. A –1 és a +1 a tökéletes összefüggést jelentené. Minél inkább megközelíti az együttható valamelyik végletet, annál erősebb a kapcsolat a két adatsor között. Pontos kiszámítását ld. például itt.

[8] A II.B rész feladatait nem minden vizsgázó oldja meg, hiszen a három feladat közül egyet mindenkinek ki kell hagynia, így az egyes feladatok megoldottságát befolyásolja az, hogy az azt kihagyók között inkább a „jobbak” vagy a „gyengébbek” voltak többségben. Ezért a továbbiakban a II.B rész feladatai megoldottságának (itt nem részletezett módon) korrigált adataival dolgozunk, amelyek figyelembe veszik a feladatokat kihagyó vizsgázói populáció összetételét is.