Német középszintű érettségi 2014 megoldás

b) Ha véletlenszerűen kiválasztjuk ennek a korlátos síkidomnak egy pontját, akkor mennyi a valószínűsége, hogy a kiválasztott pont a trapéznak is pontja lesz?

Német középszintű érettségi 2014 megoldás

Ezen az oldalon a közép és emelt szintű angol érettségi feladatsorokat találod 2005-től, vagyis az új típusú érettségi bevezetésétől kezdődően. Ezt megelőzően az angol érettségi más szerkezetű volt, ezért azokat a feladatsorokat nem közöljük. A középszintű angol érettségi egy 180 perces írásbeli és egy 15 perces szóbeli részből áll, míg emelt színten az írásbeli vizsga időtartama 240 perc, a szóbelié pedig 20 perc. Mindkét esetben az írásbeli rész olvasott szöveg értése, nyelvhelyeség, hallott szöveg értése és az íráskészség részekből áll. A hallott szöveg értése részhez természetesen tartozik egy meghallgatható angol nyelvű hanganyag is. A szóbeli vizsga társalgás, szituációs feladat (közép szint), vita (emelt szint), illetve segédanyagok segítségével történő önálló témakifejtés részekből áll. Ez utóbbi kettőhöz rövid gondolkodási időt biztosítanak. Az angol nyelv érettségi részletes leírása, a vizsgakövetelmények és a szóbeli témakörök itt érhetők el.

A táblázatban az angol írásbeli vizsga feladatlap, a hallott szöveg értését ellenőrző hanganyag, illetve az ezeket ellenőrző javítási-értékelési útmutató található minden érettségi időszakra.

Érettségi-felvételi

Érettségi-felvételi

Itt van a németérettségi megoldása: íráskészség

Itt találjátok a középszintű németérettségi negyedik részének nem hivatalos megoldását. A németérettségi nap támogatását és a feladatok megoldását köszönjük a németországi Hageni Távegyetem Budapesti Központjának!

Nehezen jöttök ki a fizetésből és az ösztöndíjból? Hat appot mutatunk, amely segíthet beosztani a pénzt

Budapesten vagy vidéken drágább diplomát szerezni?

Profi tippek kezdő egyetemistáknak: így kezelhetitek a pénzügyeiteket okosa(bba)n

Fiataloknak szóló számlacsomagok 2022-ben

Budapest, 09. 05. 2014

ich komme am 20. Juni in Berlin an. Ihr wisst ja, dass meine Tante da wohnt. Ihr Geschenk zu meinem 18-ten Geburtstag ist, dass ich bei ihr eine Geburtstagsparty mit meinen besten Freunden veranstalten kann.

So möchte ich Euch zu dieser Party recht herzlich einladen. Meine Tante wohnt in einem Einfamilienhaus. Ihr könnt im Garten zelten, dort grillen und Kesselgulasch kochen. Ihr braucht nichts mitzubringen, nur für die Musik sollt ihr sorgen.
Die Adresse ist: Tulpengasse 5

Also bis später
Euer Zoltan

Horváth János
H – 1118 Budapest
Cseresznye utca 5.

Organisation der Winzer und Bauern
Gartenfeldstr. 12 a
D – 5500 Trier

Budapest, 27.07. 2014

Sehr geehrte Damen und Herren,

ich habe Ihre Anzeige in der Frankfurter Allgemeinen Zeitung gefunden.
Ich melde mich bei Ihnen im Namen meiner MitschülerInnen.
Wir sind Schüler eines zweisprachigen Gymnasiums – 6 Mädchen und 6 Jungen -, und haben vom 3. bis zum 14. Oktober Herbstferien. In dieser Zeit könnten wir bei Ihnen arbeiten. Wir möchten am Rhein arbeiten.
Wir sprechen gut Deutsch, aber wir möchten unsere Sprachkenntnisse erweitern. Dazu wäre diese Arbeit eine gute Möglichkeit.
Ich möchte Sie fragen, ob wir bei Familien untergebracht werden, oder müssen wir selbst für Unterkunft und Verpflegung sorgen. Uns interessiert auch, wie viele Stunden wir pro Tag arbeiten müssen, und wie viel Stundenlohn wir bekommen. Sollen wir Gummistiefel und Regenjacke einpacken, wie es in der Anzeige steht?

Für eine schnelle Antwort wäre ich Ihnen recht dankbar.

Mit freundlichen Grüssen
János Horvath

Ilona Kiss
Herderplatz 4
D –47659 Oranienburg

Rollsportclub
Tübinger Platz 43
D – 47532 Berlin

Budapest, 09.05. 2014

Sehr geehrte Damen und Herren,

ich heiße Ilona Kiss, bin Ungarin, 18 Jahre alt. Jetzt erweitere ich meine Sprachkenntnisse mit dem Stipendium des Goetheinstituts in Oranienburg.
Ich habe Ihre Anzeige interessant gefunden und wurde dadurch angeregt, Inline-Skating zu lernen. Ich wollte schon auch in Ungarn sicheres Fahren, Bremsen und Fallen üben. Aber bei uns gibt es keine ähnliche Möglichkeit.
Ich möchte Sie fragen, unter welchen Bedingungen ich an diesem Kurs im Eisstadion Wilmersdorf teilnehmen kann. Bis wann muss ich mich melden, wie viel kostet der Kurs und wann fängt der Kurs an? Bitte teilen Sie mir mit, ob ich bei Ihnen die nötige Ausrüstung ausleihen kann!

Für eine schnelle Antwort wäre ich Ihnen recht dankbar.

Mit freundlichen Grüssen
Ilona Kiss

Tetszett a cikk? Kövess minket a Facebookon is, és nem fogsz lemaradni a fontos hírekről!

Pedagógia

Hazánkban az Oktatási Hivatal Sulinet osztálya koordinálja a nemzetközi ENABLE antibullying program hazai adaptációs munkáit. A pilot program hatékonyságának kvantitatív értékelése az ELTE Pedagógia és Pszichológia Karának segítségével jelenleg is zajlik, az eredmények folyamatosan publikálásra kerülnek.

Milyen a jövő osztályterme?

A jövő osztályterméről gondolkodva mindenkinek más és más jut az eszébe. Vannak, akik a technológiát vagy a digitális eszközöket helyezik középpontba, mások a különböző térbeli elrendezésekben látják a jövőt. Az is lehet, hogy a virtuális téré lesz a főszerep. Sok a kérdés, noha már léteznek konkrét elképzelések és ’minta tantermek’, ilyen például a brüsszeli Jövő Osztályterme.

Jegyzetelj okosan! – a Cornell-módszer

A jó jegyzet a tanulás alapja. A tanulmányaink során rengeteget jegyzetelünk, memorizálunk és természetesen felejtünk. Mindenkinek más a módszere, valaki színez, valaki keretez, és van olyan is, aki szóról szóra leír mindent. Természetesen ’tuti’ módszer nincs, de ha mégis szeretnél valami újat kipróbálni, akkor olvass tovább!

Érettségi 2014 – Hamarosan jön a matematika érettségi!

Nincs mit tenni, a matematika kötelező érettségi tantárgy! A diákok számára csak annyi választási lehetőség van, hogy eldönthetik: közép vagy emelt szinten szeretnének érettségizni. A két szint között a legfontosabb különbségek: középszinten csak írásbeli megmérettetés van, emelt szinten szóbeli vizsga is van; más a feladatok mennyisége és a feladatok nehézsége.

Érettségi 2014 – Felkészülés az emelt szintű matematika szóbeli vizsgára

A felsőoktatási intézmények közül egyre több kéri az emelt szintű matematika vizsgát a jelentkezőtől. A vizsgára való felkészülés más stratégiát igényel, mint a középszintű vizsga, hiszen ebben az esetben van szóbeli vizsga is. A helyzetet az is nehezíti, hogy a szóbeli vizsga tételeit nem, csak a témaköreit ismerheti meg előre a vizsgázó. A felkészülésben már magyar nyelvű Youtube videók is segítséget nyújtanak.

Projektportfólió: „The Queen reigns but does not rule.”

Hogyan hat Anglia megítélésére az ország államformája mind kül-, és belföldön? Mi a jelentősége az angol királyi/királynői szerepnek napjainkban? Egy olyan angolos projektet mutatunk be, amelyben a tanulóknak ezekre a kérdésekre kell választ találni. Cikksorozatunkban a Debreceni Egyetem tanárszakos hallgatóinak az Intel® Teach Essentials képzés keretében készült projektterveiből mutatunk be néhányat.

Német középszintű érettségi 2014 megoldás

Mai 728
Heti 7070
Havi 29486
Összes 4001152
IP: 46.98.125.27 Chrome – Windows 2022. október 13. csütörtök, 13:17

Ki van itt?

Honlapok

SULINET Matematika

Oktatási Hivatal

Versenyvizsga portál

Matematika Portálok

Berzsenyi Dániel Gimnázium


Óbudai Árpád Gimnázium


Szent István Gimnázium

A gondolkodás öröme

201. találat: Matematika emelt szintű érettségi, 2021. május I. rész, 4. feladat
Témakör: *Algebra (Azonosító: mme_202105_1r04f )

Adott az $ y = 0, 25 x( x − 5)^2;\ (0\le x \le 5) $ egyenletű görbe.
a) Igazolja, hogy az origó és az $ (5; 0) $ pont is rajta van a görbén!

Az $ ABCD $ derékszögű trapéz egyik szárának két végpontja az $ A(1; 0) $, illetve a $ B(3; 0) $ pont, a másik két csúcsa pedig a megadott görbén van, az ábra szerint. A megadott görbe és az x tengely $ [0; 5] $ szakasza egy korlátos síkidomot fog közre.

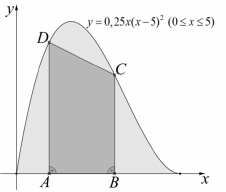
b) Ha véletlenszerűen kiválasztjuk ennek a korlátos síkidomnak egy pontját, akkor mennyi a valószínűsége, hogy a kiválasztott pont a trapéznak is pontja lesz?

202. találat: Matematika emelt szintű érettségi, 2021. május II. rész, 5. feladat
Témakör: *Algebra (Azonosító: mme_202105_2r05f )

a) Határozza meg az $ m $ valós szám összes lehetséges értékét úgy, hogy az alábbi kijelentés igaz legyen!

Az $ x^ 2 − 2 x + 4 = mx $ egyenletnek pontosan két különböző valós gyöke van.

b) Mutassa meg, hogy az alábbi kijelentés igaz!

Az $ f\ :\ \mathbb \rightarrow \mathbb;\ f ( x) = \dfrac <(1+\cos x)^2+2>$ függvény értékkészlete az $ \left[\dfrac;\dfrac \right] $ intervallum.

c) Tudjuk, hogy az $ A $,$ B $,$ C $ kijelentések mindegyike$ 0,6 $ valószínűséggel igaz és$ 0,4 $ valószínűséggel hamis. Ebben az esetben mennyi annak a valószínűsége, hogy az $ (A ∧ B) ∨ C $ kijelentés igaz?

203. találat: Matematika emelt szintű érettségi, 2021. május II. rész, 6. feladat
Témakör: *Algebra (Azonosító: mme_202105_2r06f )

Egy nyomozás során fontossá vált felderíteni azt, hogy az $ A$, $ B $, $ C $, $ D $, $ E $, $ F $ hattagú társaság mely tagjai ismerik egymást, azaz milyen a társaság ismeretségi hálója (ismeretségi gráfja). (Az ismeretség bármely két tag között kölcsönös. A társaság két ismeretségi hálója akkor különböző, ha van két olyan tag, akik az egyik hálóban egymásnak ismerősei, de a másikban nem.) A nyomozás során az már bizonyítottá vált, hogy $ A $-nak 5, $ B $-nek 4, $ C $-nek 3 ismerőse van a társaságban. Ennél többet azonban nem sikerült kideríteni, így aztán $ D $, $ E $ és $ F $ egymás közötti ismeretségeiről sincs még semmilyen információ.
a) Hányféle lehet a $ D $, $ E $, $ F $ csoport ismeretségi hálója?
A friss bizonyítékok szerint a $ D $, $ E $, $ F $ csoportban mindenki ismeri a másik két személyt.
b) Az összes eddigi (a korábban és a frissen beszerzett) információt figyelembe véve hányféle lehet az$ A$, $ B $, $ C $, $ D $, $ E $, $ F $ hattagú társaság ismeretségi hálója?
A további információk kiderítése érdekében a hattagú társaság tagjait 3 fős csoportokba szervezve hallgatják ki. Minden olyan 3 fős csoport kihallgatását megszervezik, amelyben $ A $ és $ B $ együtt nincs jelen.
c) Összesen hány ilyen csoportos kihallgatást kell szervezni?

204. találat: Matematika emelt szintű érettségi, 2021. május II. rész, 7. feladat
Témakör: *Algebra (Azonosító: mme_202105_2r07f )

Egy nyolcfős csapat kosárlabdaedzése közben mind a nyolcan 10-szer kíséreltek meg hárompontost dobni. A sikeres dobások számát mind a nyolc főnél felírták. A feljegyzett számok: 6, 3, 7, 6, 4, 7, 8 és 7.
a) Határozza meg a sikeres dobások számának átlagát, mediánját és szórását!
A kosárlabda büntetődobást 4,6 méter távolságról kell elvégezni, a gyűrű 3 méter magasan van. Petra a dobás pillanatában 2 méter magasságból engedi el a labdát, és az ideális, vízszintessel bezárt $ 45^\circ $-os szögre törekszik a dobás indításánál.
b) Petra dobásának modellezéséhez határozza meg annak a parabolának az egyenletét, amely áthalad a $ P(0; 2) $ és a $ Q(4,6; 3) $ ponton, a $ P $ pontban húzott érintőjének irányszöge pedig $ 45^\circ $! A parabola egyenletét $ y = ax^ 2 + bx + c $ alakban adja meg!

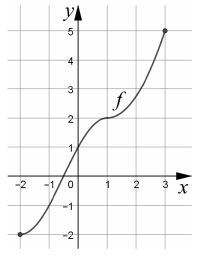
Az ábrán a $ [-2; 3] $ intervallumon értelmezett szigorúan monoton, folytonos $ f $ függvény grafikonja látható.
c) Adja meg az $ f $ inverzfüggvényének értelmezési tartományát, értékkészletét, zérushelyét, és jellemezze az inverzfüggvényt monotonitás szempontjából!

205. találat: Matematika emelt szintű érettségi, 2021. május II. rész, 8. feladat
Témakör: *Algebra (Azonosító: mme_202105_2r08f )

Egy sorsjegyből jelenleg havonta átlagosan 5000 darabot értékesítenek. Egy darab sorsjegy ára 500 Ft, de a forgalmazó cég ezt csökkenteni szeretné. A sorsjegy ára 10 Ft-os lépésekben csökkenthető. Azt feltételezik, hogy ha az ár $ n $-szer 10 Ft-tal alacsonyabb lesz, akkor havonta $ 10n^2 $-tel több sorsjegyet tudnak eladni ($ n \in \mathbb^+ $). Tekintsük ezt a feltételezést helytállónak.
a) Határozza meg a sorsjegyek eladásából származó havi bevételt, ha a sorsjegy árát 300 Ft-ra csökkentik!
b) Határozza meg azt az n értéket, amelyre a sorsjegyek eladásából származó havi bevétel maximális lenne!
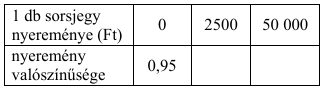
Az összes sorsjegy 5%-a nyerő. Kétféle nyeremény van: 2500 Ft-os és 50 000 Ft-os. A 2500 Ft-os nyerő sorsjegyből pontosan 24-szer annyi van, mint az 50 000 Ft-osból.
c)Töltse ki az alábbi táblázat üres mezőit, majd számítsa ki egy darab sorsjegy nyereményének várható értékét!

206. találat: Matematika emelt szintű érettségi, 2021. május II. rész, 9. feladat
Témakör: *Algebra (Azonosító: mme_202105_2r09f )

Egy teherautó raktere 2,4 méter széles, 2 méter magas és 7 méter hosszú. Ezzel a teherautóval kell olyan, méretre vágott farönköket szállítani, amelyek forgáshenger alakúak, 24 centiméter az átmérőjük, és 7 méter hosszúak. A rakomány biztonsági okokból nem nyúlhat túl a raktéren egyik irányban sem. A szállítócég az ábrán látható stratégiával rendezi el a farönköket.

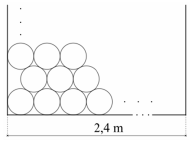
a) Mutassa meg, hogy legfeljebb 86 farönköt lehet így a raktérben elhelyezni!
b) A raktérnek hány százaléka marad üresen, ha 86 farönköt szállítanak?
Kiderült, hogy a fák egy részében megtelepedtek a szúbogarak. Bármelyik fát kiválasztva 4% annak a valószínűsége, hogy van benne szú. Az egyik vásárló cég 50 fát vett.
c) Mennyi a valószínűsége, hogy legfeljebb egy szúrágta fa kerül a rakományába?

207. találat: Matematika emelt szintű érettségi, 2021. október, I. rész, 1. feladat
Témakör: *Algebra (Azonosító: mme_202110_1r01f )

a) Oldja meg az alábbi egyenletet a valós számok halmazán!

Legyen $ f ( x) = x^2 – 9 x + 14 $ , ahol x valós szám.
Tekintsük a következő állítást: „Ha $ x > 7 $, akkor $ f (x) > 0 $.”
b) Adja meg az állítás logikai értékét (igaz vagy hamis)! Válaszát indokolja!
c) Fogalmazza meg az állítás megfordítását! Igaz-e az állítás megfordítása? Válaszát indokolja!

208. találat: Matematika emelt szintű érettségi, 2021. október, I. rész, 2. feladat
Témakör: *Algebra (Azonosító: mme_202110_1r02f )

Margiték autójában a fedélzeti számítógép kiszámítja, hogy az autó üzemanyagtartályában lévő benzin még hány kilométer megtételéhez elegendő. Nevezzük ezt hátralévő távolságnak. A számításhoz a gép a legutolsó tankolás óta mért átlagos fogyasztást veszi alapul, és úgy számol, hogy az autó a jövőben is ezzel az átlagfogyasztással fog haladni. A legutóbbi tankolás alkalmával teletöltötték az autó üzemanyagtartályát, így 45 liter benzin volt benne. A tankolás óta éppen 200 kilométert tettek meg a városban, ekkor az autó átlagfogyasztása 10 liter volt 100 kilométerenként.
a) Számítsa ki a városi autózás után a hátralévő távolságot!
A 200 kilométeres városi autóhasználatot követően Margiték egynapos autós kirándulást tettek vidéken, ezalatt összesen 100 kilométert autóztak (újabb tankolás nélkül). A kirándulás végén a kijelző alapján 200 kilométerre elegendő benzin maradt, azaz ennyi lett a hátralévő távolság.
b) Mennyi volt az autó 100 km-re vonatkozó átlagfogyasztása a kirándulás során?

209. találat: Matematika emelt szintű érettségi, 2021. október, I. rész, 3. feladat
Témakör: *Kombinatorika (Azonosító: mme_202110_1r03f )

a)Hány olyan pozitív háromjegyű szám van a tízes számrendszerben, amely a 8 és a 9 számok közül legalább az egyikkel osztható?
b) A 8-as számrendszerben háromjegyű pozitív egész számok közül véletlenszerűen kiválasztunk egyet. Mennyi a valószínűsége annak, hogy a kiválasztott szám a 9-es számrendszerben is háromjegyű?

210. találat: Matematika emelt szintű érettségi, 2021. október, I. rész, 4. feladat
Témakör: *Kombinatorika (Azonosító: mme_202110_1r04f )

Egy többnapos nemzetközi matematikakonferencia minden résztvevője belépőkártyát kap, amelyen a PQRST konvex ötszög és annak átlói láthatók.

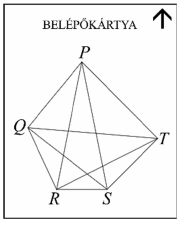
A szervezők úgy tervezik, hogy egy-egy belépőkártyán az ötszög oldalai és átlói közül valahányat (egyet vagy többet, akár az összeset, de az is lehet, hogy egyet sem) megvastagítanak, így a különböző személyek különböző ábrájú kártyát kapnak. Az elektronikus kapu optikai leolvasója ez alapján engedélyezi a belépést, és elvégzi a személy regisztrációját. (Két belépőkártya különböző, ha az egyiken szerepel olyan megvastagított szakasz, amelyik a másikon nem.) A konferenciának 400 résztvevője lesz.

a) Jut-e mindenkinek különböző belépőkártya?
A konferencia épülete egy háromszög alakú területen van. Ha a háromszög csúcsai $ A $, $ B $ és $ C $, akkor $ AB = AC = 130 $ méter, és $ BC $ = 100 méter. A háromszög alakú területet kettéosztja az egyenes $ CD $ kerítés úgy, hogy a $ BCD $ háromszög alakú rész területe $ 2000 m^2 $.

b) Milyen hosszú a CD kerítés?
A konferencián 200 magyar, 70 angol és 130 német matematikus vesz részt. Az angolok életkorának átlaga 44 év, a németeké 48 év, az összes résztvevő életkorának átlaga 45,7 év.
c) Mennyi a magyar résztvevők életkorának átlaga?

211. találat: Matematika emelt szintű érettségi, 2021. október, II. rész, 5. feladat
Témakör: *Algebra (Azonosító: mme_202110_2r05f )

Tekintsük az $ (a_n) $ sorozatot: $ a_1 = \dbinom = 1 $, $ a_2 = \dbinom = 3 $, $ a_3 = \dbinom = 6 $ és így tovább, $ a_n = \dbinom $

a) Számítsa ki az $ (a_n) $ sorozat első öt tagjából álló számsokaság átlagát és szórását!
b) A fenti $ (a_n) $ sorozatból képezzük a $ (b_n) $ sorozatot: $ b_n = \dfrac> $. Mennyi a $ (b_n) $ sorozat határértéke?
A $ (c_n) $ számtani sorozat differenciája 0,25. A sorozat első n tagjának összege 100, első $ 2n $ tagjának összege 300 ($ n \in \mathbb^+ $).
c) Határozza meg $ n $ értékét!

212. találat: Matematika emelt szintű érettségi, 2021. október, II. rész, 6. feladat
Témakör: *Geometria (Azonosító: mme_202110_2r06f )

Az ókori egyiptomiak az egyenlő szárú háromszög területét (közelítő módszerrel) úgy számolták ki, hogy az alap és a szár szorzatának a felét vették.
a) Egy egyenlő szárú háromszög alapja 18 cm hosszú. Mekkora lehet a szára, ha az ókori egyiptomiak módszere e háromszög valódi területét 25\%-nál kisebb hibával adja meg?
Az ókori Egyiptom matematikájában a számok négyzetének is jelentős szerep jutott.
b)Hány olyan 1000-nél kisebb pozitív egész szám van, amellyel az 1⋅ 2 ⋅ 3 ⋅ 4 ⋅ 5 ⋅ 6 számot megszorozva négyzetszámot kapunk?

213. találat: Matematika emelt szintű érettségi, 2021. október, II. rész, 7. feladat
Témakör: *Geometria (Azonosító: mme_202110_2r07f )

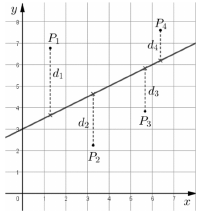
A statisztikai értékelések során szükség van az adatokat és összefüggéseket szemléltető pontok és egyenesek kölcsönös helyzetének jellemzésére. Egy ilyen jellemző lehet a pontnak egy megadott egyenestől mért függőleges távolsága.

Az ábrán látható $ P_1 $, $ P_2 $, $ P_3 $, $ P_4 $ pontok esetén a függőleges távolságok rendre a $ d_1 $, $ d_2 $, $ d_3 $, $ d_4 $ szakaszok hosszával egyenlők. (A távolságokat megadó szakaszok párhuzamosak az y tengellyel.)
a) Határozza meg az $ R(4; 2) $ és az $ S(4; 5) $ pontok függőleges távolságát az $ y = \dfracx + \dfrac$ egyenestől!
Ha a derékszögű koordináta-rendszerben az adatokat pontokkal jelenítjük meg, és különböző egyeneseket veszünk fel, akkor mindegyik egyeneshez kiszámítható a pontok függőleges távolságainak négyzetösszege (az ábrán látható példában $ d_1^2 + d_2^2 + d_3^2 + d_4^2 $ ). Tekintsük azt az egyenest a pontokra legjobban illeszkedő egyenesnek, amelyre ez a négyzetösszeg a lehető legkisebb.
Adott három pont a koordináta-rendszerben: $ A(1; 3) $, $ B(3; 5) $ és $ C(4; 4) $.
b) Adja meg az m értékét úgy, hogy az $ y = mx $ egyenletű (origón átmenő) egyenes a megadott módszer szerint a legjobban illeszkedjen az $ A $, $ B $ és $ C $ pontokra! ($ m \in \mathbb $)
Az $ y =\dfrac ( -2 x^2 + 11x) $ egyenletű $ g $ görbe áthalad a megadott $ A $ és $ B $ pontokon, a $ h $ egyenes pedig az origón és a $ C $ ponton.
c) Mekkora a $ g $ és $ h $ által közbezárt korlátos alakzat területe?

214. találat: Matematika emelt szintű érettségi, 2021. október, II. rész, 8. feladat
Témakör: *Geometria (Azonosító: mme_202110_2r08f )

Egy áruházláncban minden Kocka csokoládé vásárlásakor a csoki mellé ajándékba adnak egy „zsákbamacska” csomagot, amelyben egy kis fémkocka van. A fémkocka mindegyik lapja sárga vagy kék színűre van festve úgy, hogy mind a két színű lap előfordul.
a) Igazolja, hogy (színezés szerint) összesen 8-féle kocka van, ha a forgatással egymásba vihető színezéseket nem tekintjük különbözőnek!
b) Dórinak 7 különböző színezésű kockája van, így már csak egy hiányzik a teljes készlethez, hogy abból nyakláncot készítsen magának. Mennyi annak a valószínűsége, hogy ha 3 darab Kocka csokoládét vesz, akkor meglesz a teljes készlete? (Feltételezhetjük, hogy mindegyik kockafajta ugyanakkora valószínűséggel fordul elő a csomagokban.)

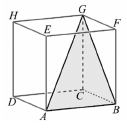
Az ábrán látható $ ABCDEFGH $ kocka élhosszúsága 10 egység.
c) Számítsa ki az $ ABG $ háromszög beírt körének sugarát!

215. találat: Matematika emelt szintű érettségi, 2021. október, II. rész, 9. feladat
Témakör: *Geometria (Azonosító: mme_202110_2r09f )

Két forgáshenger alakú viaszgyertyánk van. Az egyik gyertya alapkörének sugara $ r $, magassága $ h $, a másik alapkörének sugara $ R $, magassága szintén $ h $. A két gyertyát összeolvasztjuk, majd a viaszból egy ugyancsak $ h $ magasságú, forgáshenger alakú gyertyát öntünk ($ r, h, R > 0 $).
a) Igazolja, hogy az így kapott gyertya alapkörének sugara legalább $ \sqrt $. (Az öntés során fellépő anyagveszteségtől eltekinthetünk.)
Egy forgáshenger alakú tortát egy 15 cm sugarú, félgömb alakú védőbúra alatt helyezünk el. A torta a félgömb határoló körének síkján áll, és a torta fedőlapjának határoló köre a félgömbre illeszkedik (az ábra szerint).

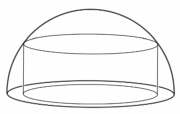
b) Igazolja, hogy az $ m $ cm magasságú torta térfogata (köbcentiméterben mérve) $ 225 π m − π m^3 $. ($ 0 < m < 15 $)
c) Igazolja, hogy a védőbúra alatt (a fent leírt módon) elhelyezhető maximális térfogatú torta térfogata kisebb, mint a félgömb térfogatának 60\%-a!

216. találat: Matematika emelt szintű érettségi, 2022. május I. rész, 1. feladat
Témakör: *Algebra (Azonosító: mme_202205_1r01f )

Oldja meg a valós számok halmazán az alábbi egyenleteket!

b) $ \dfrac\cdot \sin \left( 2x-\dfrac<\pi>\right)-\dfrac=0 $

217. találat: Matematika emelt szintű érettségi, 2022. május I. rész, 2. feladat
Témakör: *Algebra (Azonosító: mme_202205_1r02f )

a) Egy számtani sorozat első tagja 5, differenciája 3, az első $ n $ tag összege pedig 4900. Határozza meg $ n $ értékét!
b) Egy mértani sorozat első és második tagjának összege 6, harmadik és negyedik tagjának összege pedig 96. Adja meg a sorozat első tagját és hányadosát!

218. találat: Matematika emelt szintű érettségi, 2022. május I. rész, 3. feladat
Témakör: *Geometria (Azonosító: mme_202205_1r03f )

Egy társasházban 50-en laknak. A lakók $ 38\% $-a nő, $ 32\% $-a szemüveges.
a) Legalább, illetve legfeljebb hányan lehetnek a lakók között a nem szemüveges férfiak?

A társasház kertje egy 15 méter hosszú, 10 méter széles téglalap alakú földterület, amely az egyik átlója mentén ketté van osztva: az egyik fele füvesítve van, a másik felén virágágyás található. A füvesített rész derékszögű csúcsában van egy öntöző, amely egy 10 méter sugarú negyedkör alakú területet locsol a kertben.
b) Mekkora az a füvesített terület, amelyet nem ér el az öntöző?

219. találat: Matematika emelt szintű érettségi, 2022. május I. rész, 4. feladat
Témakör: *Kombinatorika (Azonosító: mme_202205_1r04f )

Egy biliárdgolyó készletben található 9 golyó tömegére a következő mérési eredményeket kapták (grammban): 163, 163, 163, 163, 163, 164, 165, 166, 166. Egy ilyen készletet akkor hitelesítenek a minőségellenőrzésen, ha az alábbi feltételek mindegyikének megfelel:
– minden golyó tömege legalább 160 gramm és legfeljebb 170 gramm;
– a golyók tömegének terjedelme legfeljebb 3 gramm;
– a golyók tömegének szórása legfeljebb 1 gramm.
a) Hitelesíthető-e ez a készlet?
Egy dobozban 3 piros és 7 kék golyó található.
b) Kihúzunk a dobozból egymás után két golyót úgy, hogy az elsőként kihúzott golyót a húzás után nem tesszük vissza. Határozza meg annak a valószínűségét, hogy a kihúzott két golyó között lesz piros!
c)Kihúzunk a 10 golyó közül egymás után három golyót úgy, hogy a kihúzott golyót a következő húzás előtt mindig visszatesszük. Legyen az $ A $ esemény az, hogy a kihúzott három golyó közül pontosan kettő piros, a $ B $ esemény pedig az, hogy a kihúzott golyók között van piros. Határozza meg a $ P(A | B) $ valószínűséget!

220. találat: Matematika emelt szintű érettségi, 2022. május II. rész, 5. feladat
Témakör: *Kombinatorika (Azonosító: mme_202205_2r05f )

Lali, Pali és Vali egy palacsintázóban ebédelnek. Lali 3 mogyorókrémes, 1 túrós és 2 fahéjas palacsintáért 1500 Ft-ot, Pali 4 mogyorókrémes, 2 túrós és 1 fahéjas palacsintáért 1740 Ft-ot, Vali pedig 1 mogyorókrémes, 2 túrós és 2 fahéjas palacsintáért 1170 Ft-ot fizetett.
a) Mennyibe kerül 1-1 darab a különböző fajta palacsintákból?
Lali vesz még egy lekváros palacsintát 210 Ft-ért. Lali zsebében 100, 50, 20, 10 és 5 Ft-os érmék vannak, mindegyikből több is. Ezek közül 6 érmét választ ki.
b) Igazolja, hogy 6 érmével három különböző módon fizethető ki 210 Ft! (Két fizetést különbözőnek tekintünk, ha legalább az egyik címletű érméből eltérő számút használunk fel a két fizetés során.)
c) Hányféle sorrendben vehet elő Lali 6 olyan érmét a zsebéből, amelyek összege 210 Ft, ha egyesével húzza elő őket? (Az azonos címletű érméket nem különböztetjük meg egymástól.)

221. találat: Matematika emelt szintű érettségi, 2022. május II. rész, 6. feladat
Témakör: *Algebra (Azonosító: mme_202205_2r06f )

Egy egyenlőszárú háromszög csúcsai a derékszögű koordináta-rendszerben $ A(0; 0) $, $ B(82; 0) $ és $ C(41; 71) $. Géza szerint ez a háromszög szabályos.
a) Határozza meg a háromszög szögeit fokban, három tizedesjegyre kerekítve!
b) Határozza meg a háromszög AC és AB oldalainak arányát négy tizedesjegyre kerekítve!
Egy csonkakúp alapkörének sugara 14 cm, fedőkörének sugara 8 cm, alkotója 10 cm hosszú. Géza szeretné gyorsan megbecsülni a csonkakúp térfogatát, ezért azt egy henger térfogatával közelíti. A közelítő henger alapkörének sugara megegyezik a csonkakúp alap- és fedőköre sugarának számtani közepével, magassága pedig egyenlő a csonkakúp magasságával.
c)Határozza meg Géza közelítésének relatív hibáját! (Relatív hibának nevezzük a közelítő értéknek a pontos értéktől mért százalékos eltérését.)

222. találat: Matematika emelt szintű érettségi, 2022. május II. rész, 7. feladat
Témakör: *Algebra (Azonosító: mme_202205_2r07f )

Flóra kétfajta lisztből süt kenyeret. A kenyérhez a recept alapján 5 : 4 arányban kell búzaliszt és rozsliszt. Eredetileg 450 gramm búzalisztet és 400 gramm rozslisztet kevert össze, de további, összesen 500 gramm liszt hozzáadásával sikerült elérnie a recept által előírt arányt.
a) A hozzáadott 500 gramm lisztből hány gramm volt a búzaliszt?
Ha egy cég $ x $ tonna lisztet állít elő egy nap alatt ($ 0 < x < 5 $), és ezt a mennyiséget el is adja, akkor egy elemzés szerint a napi nyereség értékét az $ n( x ) = 0,8 x^2 ( x - 3)(1,5 - x) $ képlet adja meg, a nyereséget tízezer tallérban számítva. (Negatív helyettesítési érték veszteséget jelent.)
b) Mutassa meg, hogy csak $ 1,5 < x < 3 $ esetén nyereséges a napi termelés!
c) Hány tallér az elérhető legnagyobb napi nyereség, és ezt hány tonna liszt (előállítása és eladása) esetén érik el?

223. találat: Matematika emelt szintű érettségi, 2022. május II. rész, 8. feladat
Témakör: *Kombinatorika (Azonosító: mme_202205_2r08f )

Egy baráti összejövetelen 7 fiú és 5 lány vett részt, találkozáskor mindenki üdvözölte a többieket. A fiúk kézfogással köszöntek egymásnak, két lány, illetve egy fiú és egy lány pedig öleléssel köszöntötte egymást.
a) Hány olyan találkozás volt, ahol öleléssel köszöntötték egymást?
Egy hatfős baráti társaság tagjai András, Bori, Csaba, Dóra, Ervin és Fanni bajnokságon döntik el, hogy ki a legjobb pingpongos közülük. Mindenki mindenki ellen egy mérkőzést játszik. Amikor 9 mérkőzést már lejátszottak, akkor kiderült, hogy mindegyikük páratlan számú mérkőzésen van túl. András az eddigi egyetlen meccsét Bori ellen játszotta, Csaba még nem játszott Ervin ellen.
b) Játszott-e már Dóra Fanni ellen?
András, Bori, Csaba és Dóra egy szabályos dobókockával dobnak egyet-egyet, és az nyer, aki a legnagyobb olyan számot dobta, amit a többiek nem dobtak (például 6, 6, 4, 1 dobások esetén a 4-est dobó játékos nyer). Ha nincs ilyen szám, akkor nem nyer senki. Bori 5-öst dobott, a többiek ezután fognak dobni.
c) Mennyi a valószínűsége annak, hogy Bori nyer?

224. találat: Matematika emelt szintű érettségi, 2022. május II. rész, 9. feladat
Témakör: *Algebra (Azonosító: mme_202205_2r09f )

Adott az $ x^2 + 2y = 16 $ egyenletű parabola és az $ x^2 + ( y – 3)^2 = 9 $ egyenletű kör.
a) Határozza meg a parabola fókuszpontjának és a kör középpontjának a koordinátáit!
b) Igazolja, hogy a $ Q (2 \sqrt< 2 >; 4) $ pont a parabolának és a körnek is pontja, és a kör $ Q $-ban
húzott érintője érinti a parabolát is!
c) Határozza meg a parabola és az $ X $ tengely által közrezárt korlátos síkidom területét!

225. találat: Matematika középszintű érettségi, 2010. május, I. rész, 1. feladat
Témakör: *Számelmélet (Azonosító: mmk_201005_1r01f )

Sorolja fel a 2010-nek mindazokat a pozitív osztóit, amelyek prímszámok!

226. találat: Matematika középszintű érettségi, 2010. május, I. rész, 2. feladat
Témakör: *Algebra (Azonosító: mmk_201005_1r02f )

Oldja meg az egyenletet a valós számok halmazán!

227. találat: Matematika középszintű érettségi, 2010. május, I. rész, 3. feladat
Témakör: *Kombinatorika (Azonosító: mmk_201005_1r03f )

Az alábbi táblázat egy 7 fős csoport tagjainak cm-ben mért magasságait tartalmazza. Mekkora a csoport átlagmagassága? A csoport melyik tagjának a magassága van legközelebb az átlagmagassághoz?

íAnna	Bea	Marci	Karcsi	Ede	Fanni	Gábor
155	158	168	170	170	174	183

228. találat: Matematika középszintű érettségi, 2010. május, I. rész, 4. feladat
Témakör: *Algebra (Azonosító: mmk_201005_1r04f )

Az $ \mathbb^+ \to \mathbb, x \to 3 +\log_2 x $ függvény az alább megadott függvények közül melyikkel azonos?

A: $ \mathbb^+ \to \mathbb, x \to 3\log_2 x $

B: $ \mathbb^+ \to \mathbb, x \to \log_2 $

C: $ \mathbb^+ \to \mathbb, x \to \log_2 $

D: $ \mathbb^+ \to \mathbb, x \to \log_2 x^3 $

229. találat: Matematika középszintű érettségi, 2010. május, I. rész, 5. feladat
Témakör: *Algebra (Azonosító: mmk_201005_1r05f )

Annának kedden 5 órája van, mégpedig matematika (M), német (N), testnevelés (T), angol (A) és biológia (B). Tudjuk, hogy a matematikaórát testnevelés követi, és az utolsó óra német. Írja le Anna keddi órarendjének összes lehetőségét!

230. találat: Matematika középszintű érettségi, 2010. május, I. rész, 6. feladat
Témakör: *Geometria (Azonosító: mmk_201005_1r06f )

Egy egyenlő szárú háromszög alapja 5 cm, a szára 6 cm hosszú. Hány fokosak a háromszög alapon fekvő szögei? A szögek nagyságát egész fokra kerekítve adja meg! Válaszát indokolja!

231. találat: Matematika középszintű érettségi, 2010. május, I. rész, 7. feladat
Témakör: *Kombinatorika (Azonosító: mmk_201005_1r07f )

Az ábrán látható hatpontú gráfba rajzoljon be 2 élt úgy, hogy a kapott gráf minden csúcsából 2 él induljon ki! A berajzolt éleket két végpontjukkal adja meg!

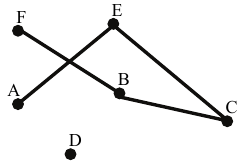
232. találat: Matematika középszintű érettségi, 2010. május, I. rész, 8. feladat
Témakör: *Kombinatorika (Azonosító: mmk_201005_1r08f )

Az alábbi kilenc szám közül egyet véletlenszerűen kiválasztva, mekkora annak a valószínűsége, hogy a kiválasztott szám nem negatív? -3,5; -5; 6; 8,4; 0; -2,5; 4; 12; -11.

233. találat: Matematika középszintű érettségi, 2010. május, I. rész, 9. feladat
Témakör: *Kombinatorika (Azonosító: mmk_201005_1r09f )

Oldja meg a valós számok halmazán a $ \sin x = 0 $ egyenletet, ha $ -2 \le x \le 2\pi $?

234. találat: Matematika középszintű érettségi, 2010. május, I. rész, 10. feladat
Témakör: *Kombinatorika (Azonosító: mmk_201005_1r10f )

Döntse el az alábbi négy állításról, hogy melyik igaz, illetve hamis!

A: Van olyan derékszögű háromszög, amelyben az egyik hegyesszög szinusza $ \dfrac < 2>$ .

B: Ha egy háromszög egyik hegyesszögének szinusza $ \dfrac < 2>$ , akkor a háromszög derékszögű.

C: A derékszögű háromszögnek van olyan szöge, amelynek nincs tangense.

D: A derékszögű háromszögek bármelyik szögének értelmezzük a koszinuszát.

235. találat: Matematika középszintű érettségi, 2010. május, I. rész, 11. feladat
Témakör: *Kombinatorika (Azonosító: mmk_201005_1r11f )

A héten az ötös lottón a következő számokat húzták ki: 10, 21, 22, 53 és 87. Kata elújságolta Sárának, hogy a héten egy két találatos szelvénye volt. Sára nem ismeri Kata szelvényét, és arra tippel, hogy Kata a 10-est és az 53-ast találta el. Mekkora annak a valószínűsége, hogy Sára tippje helyes? Válaszát indokolja!

236. találat: Matematika középszintű érettségi, 2010. május, I. rész, 12. feladat
Témakör: *Kombinatorika (Azonosító: mmk_201005_1r12f )

Egy 17 fős csoport matematika témazáró dolgozatának értékelésekor a tanár a következő információkat közölte: Mind a 17 dolgozatot az 1-es, a 2-es, a 3-as, a 4-es és az 5-ös jegyek valamelyikével osztályozta. A jegyek mediánja 4, módusza 4, terjedelme 4 és az átlaga (két tizedes jegyre kerekítve) 3,41. Döntse el, hogy az alábbi állítások közül melyik igaz, illetve hamis!

A: A dolgozatoknak több mint a fele jobb hármasnál.

B: Nincs hármasnál rosszabb dolgozat.

237. találat: Matematika középszintű érettségi, 2010. május, II. rész, 13. feladat
Témakör: *Algebra (Azonosító: mmk_201005_2r13f )

Számítsa ki azt a két pozitív számot, amelyek számtani (aritmetikai) közepe 8, mértani (geometriai) közepe pedig 4,8.

238. találat: Matematika középszintű érettségi, 2010. május, II. rész, 14. feladat
Témakör: *Geometria (Azonosító: mmk_201005_2r14f )

Az $ ABC $ háromszög csúcspontjainak koordinátái: $ A(0; 0), B(–2; 4), C(4; 5) $.

a) Írja fel az $ A $B oldal egyenesének egyenletét!

b) Számítsa ki az $ ABC$ háromszög legnagyobb szögét! A választ tized fokra kerekítve adja meg!

c) Számítsa ki az $ ABC $ háromszög területét!

239. találat: Matematika középszintű érettségi, 2010. május, II. rész, 15. feladat
Témakör: *Geometria (Azonosító: mmk_201005_2r15f )

a) Rajzolja meg derékszögű koordinátarendszerben a $ ]−1;6 ] $ intervallumon értelmezett, $ -\left|x-2 \right|+3 $ hozzárendelésű függvény grafikonját!

b) Állapítsa meg a függvény értékkészletét, és adja meg az összes zérushelyét!

c) Döntse el, hogy a $ P(3,2 ; 1,85) $ pont rajta van-e a függvény grafikonján! Válaszát számítással indokolja!

d) Töltse ki az alábbi táblázatot, és adja meg a függvényértékek (a hét szám) mediánját!

240. találat: Matematika középszintű érettségi, 2010. május, II. rész, 16. feladat
Témakör: *Kombinatorika (Azonosító: mmk_201005_2r16f )

Egy középiskolába 620 tanuló jár. Az iskola diákbizottsága az iskolanapra három kiadványt jelentetett meg:

I. Diákok Hangja

III. Miénk a suli!

Később felmérték, hogy ezeknek a kiadványoknak milyen volt az olvasottsága az iskola tanulóinak körében. A Diákok Hangját a tanulók $ 25\% $-a, az Iskolaéletet $ 40\% $-a, a Miénk a suli! c. kiadványt pedig $ 45\% $-a olvasta. Az első két kiadványt a tanulók $ 10\% $-a, az első és harmadik kiadványt $ 20\% $-a, a másodikat és harmadikat $ 25\% $-a, mindhármat pedig $ 5\% $-a olvasta.

a) Hányan olvasták mindhárom kiadványt?

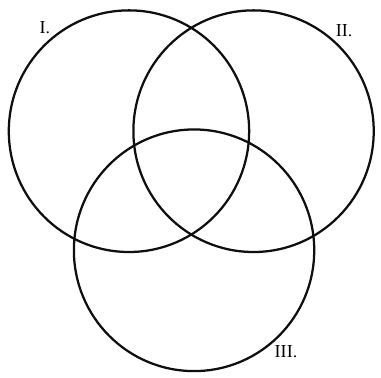
b) A halmazábra az egyes kiadványokat elolvasott tanulók létszámát szemlélteti. Írja be a halmazábra mindegyik tartományába az oda tartozó tanulók számát!

c) Az iskola tanulóinak hány százaléka olvasta legalább az egyik kiadványt?

Az iskola 12. évfolyamára 126 tanuló jár, közöttük kétszer annyi látogatta az iskolanap rendezvényeit, mint aki nem látogatta. Az Iskolaélet című kiadványt a rendezvényeket látogatók harmada, a nem látogatóknak pedig a fele olvasta. Egy újságíró megkérdez két, találomra kiválasztott diákot az évfolyamról, hogy olvasták-e az Iskolaéletet.

d) Mekkora annak a valószínűsége, hogy a két megkérdezett diák közül az egyik látogatta az iskolanap rendezvényeit, a másik nem, viszont mindketten olvasták az Iskolaéletet?

241. találat: Matematika középszintű érettségi, 2010. május, II. rész, 17. feladat
Témakör: *Kombinatorika (Azonosító: mmk_201005_2r17f )

Statisztikai adatok szerint az 1997-es év utáni években 2003-mal bezárólag a világon évente átlagosan $ 1,1\% $-kal több autót gyártottak, mint a megelőző évben. A 2003-at követő években, egészen 2007-tel bezárólag évente átlagosan már $ 5,4\% $-kal gyártottak többet, mint a megelőző évben. 2003-ban összesen 41,9 millió autó készült.

a) Hány autót gyártottak a világon 2007-ben?

b) Hány autót gyártottak a világon 1997-ben? Válaszait százezerre kerekítve adja meg!

2008-ban az előző évhez képest csökkent a gyártott autók száma, ekkor a világon összesen 48,8 millió új autó hagyta el a gyárakat. 2008-ban előrejelzés készült a következő 5 évre vonatkozóan. Eszerint 2013-ban 38 millió autót fognak gyártani. Az előrejelzés úgy számolt, hogy minden évben az előző évinek ugyanakkora százalékával csökken a termelés.

c) Hány százalékkal csökken az előrejelzés szerint az évenkénti termelés a 2008-at követő 5 év során? Az eredményt egy tizedes jegyre kerekítve adja meg!

d) Elfogadjuk az előrejelzés adatát, majd azt feltételezzük, hogy 2013 után évente $ 3\% $-kal csökken a gyártott autók száma. Melyik évben lesz így az abban az évben gyártott autók száma a 2013-ban gyártottaknak a $ 76\% $-a?

242. találat: Matematika középszintű érettségi, 2010. május, II. rész, 18. feladat
Témakör: *Geometria (Azonosító: mmk_201005_2r18f )

Az egyik csokoládégyárban egy újfajta, kúp alakú desszertet gyártanak. A desszert csokoládéból készült váza olyan, mint egy tölcsér. (Lásd ábra.) A külső és belső kúp hasonló, a hasonlóság aránya $ \dfrac < 5>$ . A kisebb kúp adatai: alapkörének sugara 1 cm, magassága 2,5 cm hosszú.

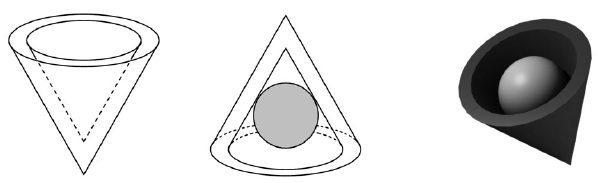
a) Hány cm3 csokoládét tartalmaz egy ilyen csokoládéváz? A választ tizedre kerekítve adja meg!

Az elkészült csokoládéváz üreges belsejébe marcipángömböt helyeznek, ezután egy csokoládéból készült vékony körlemezzel lezárják a kúpot.

b) Hány cm a sugara a lehető legnagyobb méretű ilyen marcipángömbnek? A választ tizedre kerekítve adja meg!

A marcipángömböket gyártó gép működése nem volt hibátlan. A mintavétellel végzett minőség-ellenőrzés kiderítette, hogy a legyártott gömbök $ 10\% $-ában a marcipángömb mérete nem felel meg az előírtnak.

c) A már legyártott nagy mennyiségű gömb közül 10-et kiválasztva, mekkora annak a valószínűsége, hogy a kiválasztottak között pontosan 4-nek a mérete nem felel meg az előírásnak? (A kérdezett valószínűség kiszámításához használhatja a binomiális eloszlás képletét.)

243. találat: Matematika középszintű érettségi, 2010. október, I. rész, 1. feladat
Témakör: *Kombinatorika (Azonosító: mmk_201010_1r01f )

Adott az $ A $ és $ B $ halmaz: $ A = \ $, $ B =\. $ Adja meg elemeik felsorolásával az $ A \cap B $ és $ A \cup B $ halmazokat!

244. találat: Matematika középszintű érettségi, 2010. október, I. rész, 2. feladat
Témakör: *Kombinatorika (Azonosító: mmk_201010_1r02f )

Egy baráti társaság minden tagja írt egy-egy SMS üzenetet a társaság minden további tagjának. Így mindenki 11 üzenetet írt. Hány SMS-t írtak egymásnak összesen a társaság tagjai?

245. találat: Matematika középszintű érettségi, 2010. október, I. rész, 3. feladat
Témakör: *Algebra (Azonosító: mmk_201010_1r03f )

Három egyenes egyenlete a következő ( $ a $ és $ b $ valós számokat jelölnek):

Milyen számot írjunk az $ a $ helyére, hogy az $ e $ és $ f $ egyenesek párhuzamosak legyenek? Melyik számot jelöli $ b $, ha a $ g $ egyenes merőleges az $ e $ egyenesre?

246. találat: Matematika középszintű érettségi, 2010. október, I. rész, 4. feladat
Témakör: *Algebra (Azonosító: mmk_201010_1r04f )

Mely valós számokra értelmezhető a $ \sqrt >$ kifejezés?

247. találat: Matematika középszintű érettségi, 2010. október, I. rész, 5. feladat
Témakör: *Algebra (Azonosító: mmk_201010_1r05f )

Milyen valós számokat jelöl az $ a $, ha tudjuk, hogy a valós számok halmazán értelmezett $ x \to a^x $ függvény szigorúan monoton növekvő?

248. találat: Matematika középszintű érettségi, 2010. október, I. rész, 6. feladat
Témakör: *Algebra (Azonosító: mmk_201010_1r06f )

Válassza ki az $ A $ halmaz elemei közül azokat a számokat, amelyek megoldásai a $ \sqrt < x^ 2 >= – x $egyenletnek! $ A = \ $

249. találat: Matematika középszintű érettségi, 2010. október, I. rész, 7. feladat
Témakör: *Geometria (Azonosító: mmk_201010_1r07f )

Tekintsük azt a derékszögű háromszöget, amelyben az átfogó hossza 1, az $ \alpha $ hegyesszög melletti befogó hossza pedig $ \sin \alpha $. Mekkora az $ \alpha $ szög? Válaszát indokolja!

250. találat: Matematika középszintű érettségi, 2010. október, I. rész, 8. feladat
Témakör: *Számelmélet (Azonosító: mmk_201010_1r08f )

Döntse el, hogy az alábbi állítások közül melyik igaz és melyik hamis!

I. Minden prímszám páratlan.

II. Létezik páratlan prímszám.

III. Minden egész szám racionális szám.

IV. Van olyan irracionális szám, amelyik felírható két egész szám hányadosaként.

251. találat: Matematika középszintű érettségi, 2010. október, I. rész, 9. feladat
Témakör: *Algebra (Azonosító: mmk_201010_1r09f )

A $ b $, $ c $ és $ d $ pozitív számokat jelölnek. Tudjuk, hogy $ \lg b = \dfrac<\lg c-\lg d>3 $ Fejezze ki az egyenlőségből $ b $-t úgy, hogy abban $ c $ és $ d $ logaritmusa ne szerepeljen!

252. találat: Matematika középszintű érettségi, 2010. október, I. rész, 10. feladat
Témakör: *Algebra (Azonosító: mmk_201010_1r10f )

Adja meg képlettel egy olyan, a valós számok halmazán értelmezett függvény hozzárendelési utasítását, amelynek (abszolút) maximuma van! A megadott függvénynek állapítsa meg a maximumhelyét is!

253. találat: Matematika középszintű érettségi, 2010. október, I. rész, 11. feladat
Témakör: *Kombinatorika (Azonosító: mmk_201010_1r11f )

A diákönkormányzat újonnan választott négytagú vezetősége: Kata, Mari, Réka és Bence. Közülük Kata három, Réka és Bence pedig két-két vezetőségi tagot ismert korábbról. Mari a négyes csoportnak csak egy tagját ismerte. (Az ismeretségek kölcsönösek.) Rajzolja fel a négytagú vezetőség választás előtti ismeretségi gráfját!

254. találat: Matematika középszintű érettségi, 2010. október, I. rész, 12. feladat
Témakör: *Algebra (Azonosító: mmk_201010_1r12f )

Egy kör az $ (1; 0) $ és $ (7; 0) $ pontokban metszi az x tengelyt. Tudjuk, hogy a kör középpontja az $ y = x $ egyenletű egyenesre illeszkedik. Írja fel a kör középpontjának koordinátáit! Válaszát indokolja!

255. találat: Matematika középszintű érettségi, 2010. október, II. rész, 13. feladat
Témakör: *Algebra (Azonosító: mmk_201010_2r13f )

Oldja meg a valós számok halmazán a következő egyenlőtlenségeket!

a) $ x-\dfrac 2 > \dfrac 4 – \dfrac 3 $

Mindkét esetben ábrázolja a megoldáshalmazt számegyenesen!

256. találat: Matematika középszintű érettségi, 2010. október, II. rész, 14. feladat
Témakör: *Geometria (Azonosító: mmk_201010_2r14f )

Az iskolatejet gúla alakú, impregnált papírból készült dobozba csomagolják. (Lásd az alábbi ábrát, ahol $ CA = CB = CD $ .)

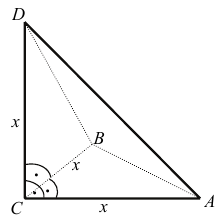
A dobozba 2,88 dl tej fér.

a) Számítsa ki a gúla éleinek hosszát! Válaszát egész $ cm $-ben adja meg!

b) Mekkora a papírdoboz felszíne? Válaszát $ cm^2 $-ben, egészre kerekítve adja meg!

257. találat: Matematika középszintű érettségi, 2010. október, II. rész, 15. feladat
Témakör: *Kombinatorika (Azonosító: mmk_201010_2r15f )

Egy kockajátékban egy menet abból áll, hogy szabályos dobókockával kétszer dobunk egymás után. Egy dobás 1 pontot ér, ha négyest, vagy ötöst dobunk, egyébként a dobásért nem jár pont. A menetet úgy pontozzák, hogy a két dobásért járó pontszámot összeadják.

a) Mennyi annak a valószínűsége, hogy egy menetben 1 pontot szerzünk, és azt az első dobásért kapjuk?

b) Minek nagyobb a valószínűsége,

– annak, hogy egy menetben szerzünk pontot, vagy

– annak, hogy egy menetben nem szerzünk pontot?

258. találat: Matematika középszintű érettségi, 2010. október, II. rész, 16. feladat
Témakör: *Algebra (Azonosító: mmk_201010_2r16f )

a) Egy számtani sorozat első tagja -7, a nyolcadik tagja 14. Adja meg n lehetséges értékeit, ha a sorozat első n tagjának összege legfeljebb 660.

b) Egy mértani sorozat első tagja ugyancsak -7, a negyedik tagja -189. Mekkora az n, ha az első n tag összege -68 887?

259. találat: Matematika középszintű érettségi, 2010. október, II. rész, 17. feladat
Témakör: *Geometria (Azonosító: mmk_201010_2r17f )

Az ábrán egy ejtőernyős klub kitűzője látható. (Az egyik körív középpontja a szabályos háromszög A csúcsa, a másik körív középpontja az A csúccsal szemközti oldal felezőpontja.) Ezt a lapot fogják tartományonként színesre festeni.

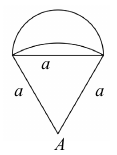
a) A Számítsa ki egyenként mindhárom tartomány területét, ha a = 2,5 cm ! Számításait legalább két tizedesjegy pontossággal végezze, és az így kapott eredményt egy tizedesjegyre kerekítve adja meg!

b) Hányféle módon festhető színesre a kitűző, ha minden tartományt a piros, sárga, zöld és kék színek valamelyikére festenek a következő két feltétel együttes figyelembe vételével:

(1) szomszédos tartományok nem lehetnek azonos színűek;

(2) piros és sárga színű tartomány nem lehet egymás mellett. (Szomszédos tartományoknak van közös határvonala.)

260. találat: Matematika középszintű érettségi, 2010. október, II. rész, 18. feladat
Témakör: *Kombinatorika (Azonosító: mmk_201010_2r18f )

Megkérdeztek 25 családot arról, hogy hány forintot költöttek az elmúlt hónapban friss gyümölcsre. A felmérés eredményét mutatja az alábbi táblázat:

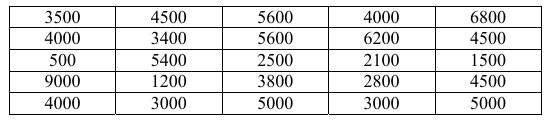
(Az adatokat tekintsük pontos értékeknek!)

a) Hány forintot költöttek átlagosan ezek a családok friss gyümölcs vásárlására az elmúlt hónapban?

b) Ossza 1000 Ft terjedelmű osztályokba a fenti értékeket, kezdve a 0-1000 Ft, 1001-2000 Ft stb. osztályokkal, és ábrázolja ezeknek az osztályoknak a gyakoriságát oszlopdiagramon!

c) Az 500 Ft és a 9000 Ft kiugró értékek. Mennyi a megmaradt adatok átlaga, ha ezeket a kiugró értékeket elhagyjuk az adatok közül? Hány százalékos változást jelent ez az eredeti átlaghoz képest, és milyen irányú ez a változás? Mennyi az így keletkezett új adatsor terjedelme?

(Azátlagot forintra, a százaléklábat két tizedesjegyre kerekítve adja meg!)

d) Az eredeti mintát a vizsgálatot végző cég két új család megfelelő adatával bővítette. Az egyik az eredeti átlagnál 1000 Ft-tal többet, a másik ugyanennyivel kevesebbet költött havonta friss gyümölcsre. Mutassa meg számítással, hogy így az átlag nem változott!

261. találat: Matematika középszintű érettségi, 2011. május, I. rész, 1. feladat
Témakör: *Algebra ( nevezetes azonosság, egyszerűsítés) (Azonosító: mmk_201105_1r01f )

Egyszerűsítse a következő törtet, ahol $b \neq 6$.

262. találat: Matematika középszintű érettségi, 2011. május, I. rész, 2. feladat
Témakör: *Valószínűségszámítás ( kombinatorika) (Azonosító: mmk_201105_1r02f )

A 2, 4 és 5 számjegyek mindegyikének felhasználásával elkészítjük az összes, különböző számjegyekből álló háromjegyű számot. Ezek közül véletlenszerűen kiválasztunk egyet. Mennyi annak a valószínűsége, hogy az így kiválasztott szám páratlan? Válaszát indokolja!

263. találat: Matematika középszintű érettségi, 2011. május, I. rész, 3. feladat
Témakör: *Térgeometria ( hasonlóság) (Azonosító: mmk_201105_1r03f )

Hányszorosára nő egy kocka térfogata, ha minden élét háromszorosára növeljük?

264. találat: Matematika középszintű érettségi, 2011. május, I. rész, 4. feladat
Témakör: *Oszthatóság ( számelmélet, LNKO, LKKT) (Azonosító: mmk_201105_1r04f )

Adottak a következő számok: $a=2^3 \cdot 5 \cdot 7^2 \cdot 11^4$ és $b=2 \cdot 5^2 \cdot 11^3 \cdot 15$. Írja fel a és b legnagyobb közös osztóját és legkisebb közös többszörösét! A kért számokat elegendő prímtényezős alakban megadni.

265. találat: Matematika középszintű érettségi, 2011. május, I. rész, 5. feladat
Témakör: *Függvények ( trigonometria) (Azonosító: mmk_201105_1r05f )

A következő két függvény mindegyikét a valós számok halmazán értelmezzük: $f(x)= \sin x; \quad g(x)=\sin 3x$. Adja meg mindkét függvény értékkészletét!

266. találat: Matematika középszintű érettségi, 2011. május, I. rész, 6. feladat
Témakör: *Algebra ( másodfokú) (Azonosító: mmk_201105_1r06f )

Mekkora az $x^2-6,5x-3,5=0$ egyenlet valós gyökeinek összege, illetve szorzata? Válaszát indokolja!

267. találat: Matematika középszintű érettségi, 2011. május, I. rész, 7. feladat
Témakör: *Halmazok ( metszet, különbség) (Azonosító: mmk_201105_1r07f )

Az A halmaz az 5-re végződő kétjegyű pozitív egészek halmaza, a B halmaz pedig a kilenccel osztható kétjegyű pozitív egészek halmaza. Adja meg elemeik felsorolásával az alábbi halmazokat:

$A; \quad B; \quad A \cap B; \quad A \setminus B$

268. találat: Matematika középszintű érettségi, 2011. május, I. rész, 8. feladat
Témakör: *Algebra ( exponenciális) (Azonosító: mmk_201105_1r08f )

Adja meg az alábbi két egyenlet valós gyökeit!

a) $ 5^=625$

b) $ 2^y = \dfrac$

269. találat: Matematika középszintű érettségi, 2011. május, I. rész, 9. feladat
Témakör: *Algebra ( logaritmus, trigonometria) (Azonosító: mmk_201105_1r09f )

Melyik szám nagyobb?

$A= \lg \dfrac$ vagy $B=\cos 8\pi$

270. találat: Matematika középszintű érettségi, 2011. május, I. rész, 10. feladat
Témakör: *Algebra ( abszolútérték) (Azonosító: mmk_201105_1r10f )

Oldja meg a valós számok halmazán a következő egyenletet!

271. találat: Matematika középszintű érettségi, 2011. május, I. rész, 11. feladat
Témakör: *Sorozatok ( algebra, számtani sorozat) (Azonosító: mmk_201105_1r11f )

Melyik a 201-edik pozitív páros szám? Válaszát indokolja!

272. találat: Matematika középszintű érettségi, 2011. május, I. rész, 12. feladat
Témakör: *Logika ( algebra, geometria) (Azonosító: mmk_201105_1r12f )

Döntse el az alábbi állítások mindegyikéről, hogy igaz-e vagy hamis!

A: Ha két szám négyzete egyenlő, akkor a számok is egyenlők.

B: A kettes számrendszerben felírt 10100 szám a tízes számrendszerben 20.

C: Egy hat oldalú konvex sokszögnek 6 átlója van.

273. találat: Matematika középszintű érettségi, 2011. május, II. rész, 13. feladat
Témakör: *statisztika (medián, átlag, diagram, grafikon) (Azonosító: mmk_201105_2r13f )

Egy iskolai tanulmányi verseny döntőjébe 30 diák jutott be, két feladatot kellett megoldaniuk. A verseny után a szervezők az alábbi oszlopdiagramokon ábrázolták az egyes feladatokban szerzett pontszámok eloszlását:

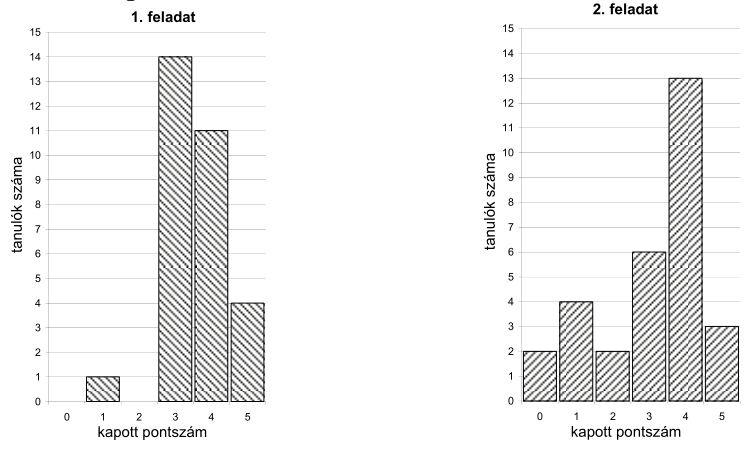
a) A diagramok alapján töltse ki a táblázat üres mezőit! Az első feladatra kapott pontszámok átlagát két tizedes jegyre kerekítve adja meg!

b) A megfelelő középponti szögek megadása után ábrázolja kördiagramon a 2. feladatra kapott pontszámok eloszlását!

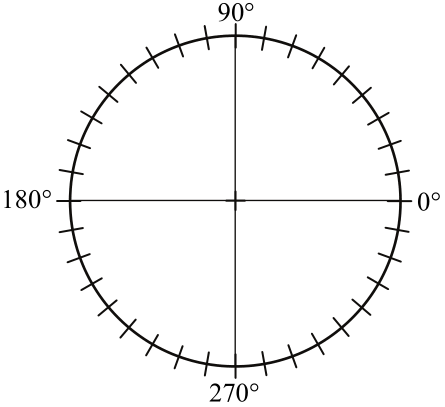
c) A versenyen minden tanuló elért legalább 3 pontot. Legfeljebb hány olyan tanuló lehetett a versenyzők között, aki a két feladat megoldása során összesen pontosan 3 pontot szerzett?

274. találat: Matematika középszintű érettségi, 2011. május, II. rész, 14. feladat
Témakör: *Sorozatok (mértani sorozat) (Azonosító: mmk_201105_2r14f )

Egy autó ára újonnan 2 millió 152 ezer forint, a megvásárlása után öt évvel ennek az autónak az értéke 900 ezer forint.

a) A megvásárolt autó tulajdonosának a vezetési biztonságát a vásárláskor 90 ponttal jellemezhetjük. Ez a vezetési biztonság évente az előző évinek 6 %-ával nő. Hány pontos lesz 5 év elteltével az autótulajdonos vezetési biztonsága? Válaszát egész pontra kerekítve adja meg!

b) Az első öt év során ennek az autónak az értéke minden évben az előző évi értékének ugyanannyi százalékával csökken. Hány százalék ez az éves csökkenés? Válaszát egész százalékra kerekítve adja meg!

275. találat: Matematika középszintű érettségi, 2011. május, II. rész, 15. feladat
Témakör: *Koordinátageometria (skaláris szorzat, koszinusztétel, egyenlő szárú, tangens) (Azonosító: mmk_201105_2r15f )

Az ABC háromszög csúcsainak koordinátái: A(-3; 2); B(3; 2); és C(0;0).

a) Számítsa ki az ABC háromszög szögeit!

b) Írja fel az ABC háromszög körülírt körének egyenletét!

276. találat: Matematika középszintű érettségi, 2011. május, II. rész, 16. feladat
Témakör: *Térgeometria (henger, kúp, kettőskúp) (Azonosító: mmk_201105_2r16f )

Egy 12 cm oldalhosszúságú négyzetet megforgatunk az egyik oldalával párhuzamos szimmetriatengelye körül.

a) Mekkora az így keletkező forgástest térfogata és felszíne? A felszínt egész $ cm^2 $-re, a térfogatot egész $ cm^3 $-re kerekítve adja meg!

Ugyanezt a négyzetet forgassuk meg az egyik átlóját tartalmazó forgástengely körül!

b) Mekkora az így keletkező forgástest térfogata és felszíne? A felszínt egész $ cm^2 $-re, a térfogatot egész $ cm^3 $-re kerekítve adja meg!

c) A forgástestek közül az utóbbinak a felszíne hány százaléka az első forgatással kapott forgástest felszínének?

277. találat: Matematika középszintű érettségi, 2011. május, II. rész, 17. feladat
Témakör: *Algebra (logaritmus, egyenlet, helyettesítési érték) (Azonosító: mmk_201105_2r17f )

Egy új típusú, az alacsonyabb nyomások mérésére kifejlesztett műszer tesztelése során azt tapasztalták, hogy a műszer által mért $ p_m $ és a valódi $ p_v $ nyomás között a $ \lg p_m=0,8 \cdot \lg p_v+0,301 $ összefüggés áll fenn. A műszer által mért és a valódi nyomás egyaránt pascal (Pa) egységekben szerepel a képletben.

a) Mennyit mér az új műszer 20 Pa valódi nyomás esetén?

b) Mennyi valójában a nyomás, ha a műszer 50 Pa értéket mutat?

c) Mekkora nyomás esetén mutatja a műszer a valódi nyomást?

A pascalban kiszámított értékeket egész számra kerekítve adja meg!

278. találat: Matematika középszintű érettségi, 2011. május, II. rész, 18. feladat
Témakör: *Kombinatorika (valószínűségszámítás) (Azonosító: mmk_201105_2r18f )

András, Balázs, Cili, Dóra és Enikő elhatározták, hogy sorsolással döntenek arról, hogy közülük ki kinek készít ajándékot. Úgy tervezték, hogy a neveket ráírják egy-egy papírcetlire, majd a lefelé fordított öt cédulát összekeverik, végül egy sorban egymás mellé leteszik azokat az asztalra. Ezután, keresztnevük szerinti névsorban haladva egymás után vesznek el egy-egy cédulát úgy, hogy a soron következő mindig a bal szélső cédulát veszi el.

a) Mennyi a valószínűsége, hogy az elsőnek húzó Andrásnak a saját neve jut?

b) Írja be az alábbi táblázatba az összes olyan sorsolás eredményét, amelyben csak Enikőnek jut a saját neve! A táblázat egyes soraiban az asztalon lévő cédulák megfelelő sorrendjét adja meg! (A megadott táblázat sorainak a száma lehet több, kevesebb vagy ugyanannyi, mint a felsorolandó esetek száma. Ennek megfelelően hagyja üresen a felesleges mezőket, vagy egészítse ki újabb mezőkkel a táblázatot, ha szükséges!)

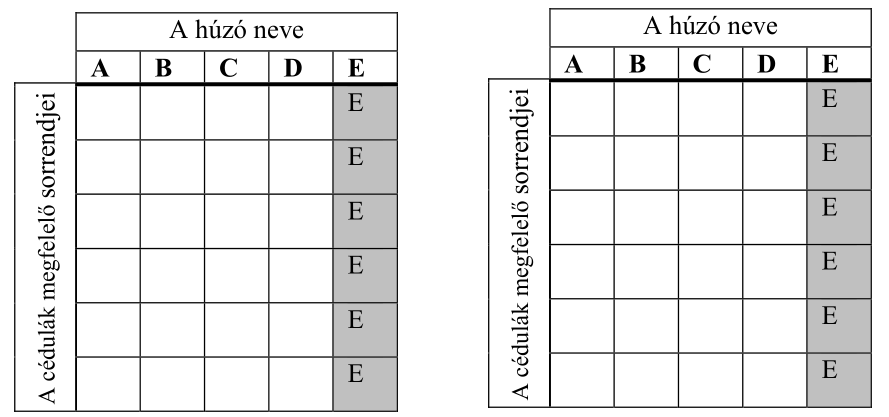
c) Az ajándékok átadása után mind az öten moziba mentek, és a nézőtéren egymás mellett foglaltak helyet. Hány különböző módon kerülhetett erre sor, ha tudjuk, hogy a két fiú nem ült egymás mellett?

279. találat: Matematika középszintű érettségi, 2011. október, I. rész, 1. feladat
Témakör: *Számelmélet ( prím) (Azonosító: mmk_201110_1r01f )

Írja fel prímszámok szorzataként a 420-at!

280. találat: Matematika középszintű érettségi, 2011. október, I. rész, 2. feladat
Témakör: *Algebra ( arány) (Azonosító: mmk_201110_1r02f )

Bontsa fel a 36 000-et két részre úgy, hogy a részek aránya 5 : 4 legyen!

281. találat: Matematika középszintű érettségi, 2011. október, I. rész, 3. feladat
Témakör: *Sorozatok ( algebra, mértani sorozat) (Azonosító: mmk_201110_1r03f )

Egy sejttenyészetben 2 naponta kétszereződik meg a sejtek száma. Az első nap kezdetén 5000 sejtből állt a tenyészet. Hány sejt lesz a tenyészetben 8 nap elteltével? Számításait részletezze!

282. találat: Matematika középszintű érettségi, 2011. október, I. rész, 4. feladat
Témakör: *Halmazok ( halmazművelet) (Azonosító: mmk_201110_1r04f )

Jelölje $\mathbb$ a természetes számok halmazát, $\mathbb$ az egész számok halmazát és $\varnothing$ az üres halmazt! Adja meg az alábbi halmazműveletek eredményét!

a) $\mathbb\cap \mathbb$

b) $\mathbb\cup \varnothing $

c) $\varnothing \setminus \mathbb$

283. találat: Matematika középszintű érettségi, 2011. október, I. rész, 5. feladat
Témakör: *Függvények ( abszolútérték, paraméter) (Azonosító: mmk_201110_1r05f )

Az ábrán a valós számok halmazán értelmezett $f(x)= \left | x+a \right |+b$ függvény grafikonjának egy részlete látható. Adja meg a és b értékét!

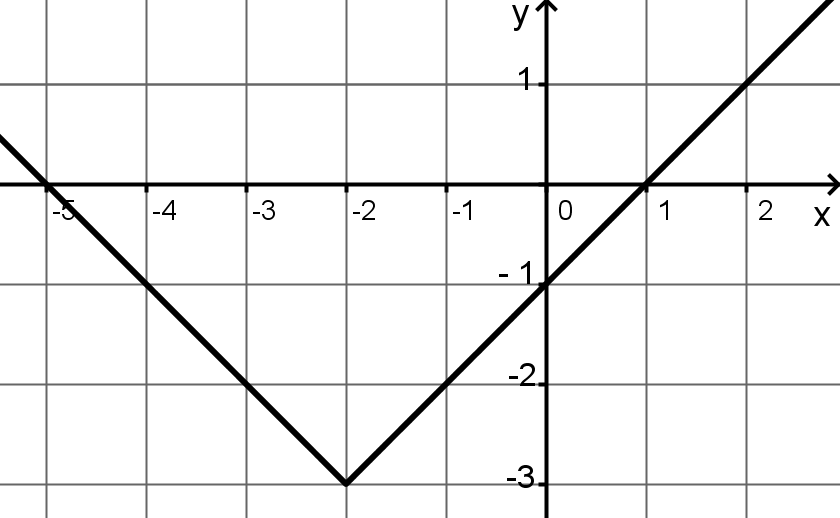
284. találat: Matematika középszintű érettségi, 2011. október, I. rész, 6. feladat
Témakör: *Statisztika (Azonosító: mmk_201110_1r06f )

Adja meg a 2; 11; 7; 3; 17; 5; 13 számok mediánját!

285. találat: Matematika középszintű érettségi, 2011. október, I. rész, 7. feladat
Témakör: *Kombinatorika ( gráfok) (Azonosító: mmk_201110_1r07f )

Rajzoljon le egy 4 pontú egyszerű gráfot, amelyben a pontok fokszáma rendre 3, 2, 2, 1!

286. találat: Matematika középszintű érettségi, 2011. október, I. rész, 8. feladat
Témakör: *Sorozatok (Azonosító: mmk_201110_1r08f )

Egy számtani sorozat ötvenedik tagja 29, az ötvenegyedik tagja 26. Számítsa ki a sorozat első tagját!

287. találat: Matematika középszintű érettségi, 2011. október, I. rész, 9. feladat
Témakör: *Algebra ( azonosság) (Azonosító: mmk_201110_1r09f )

Ha $a \neq 1$ , akkor az alábbi egyenletek közül melyik azonosság?

288. találat: Matematika középszintű érettségi, 2011. október, I. rész, 10. feladat
Témakör: *Függvények ( logaritmus) (Azonosító: mmk_201110_1r10f )

István az $x \mapsto \log_>x$ $x > 0$ függvény grafikonját akarta felvázolni, de ez nem sikerült neki, több hibát is elkövetett (a hibás vázlat látható a mellékelt ábrán).

Döntse el, hogy melyik igaz az alábbi állítások közül!

A) István rajzában hiba az, hogy a vázolt függvény szigorúan monoton csökkenő.

B) István rajzában hiba az, hogy a vázolt függvény 2-höz –2-t rendel.

C) István rajzában hiba az, hogy a vázolt függvény zérushelye 1.

289. találat: Matematika középszintű érettségi, 2011. október, I. rész, 11. feladat
Témakör: *Sorozatok ( mértani sorozat, logaritmus) (Azonosító: mmk_201110_1r11f )

A 2000 eurós tőke évi 6 %-os kamatos kamat mellett hány teljes év elteltével nőne 4024 euróra? Megoldását részletezze!

290. találat: Matematika középszintű érettségi, 2011. október, I. rész, 12. feladat
Témakör: *Térgeometria (Azonosító: mmk_201110_1r12f )

Az ábrán látható kockának berajzoltuk az egyik lapátlóját. Rajzoljon ebbe az ábrába egy olyan másik lapátlót, amelynek van közös végpontja a berajzolt lapátlóval! Hány fokos szöget zár be ez a két lapátló? Válaszát indokolja!

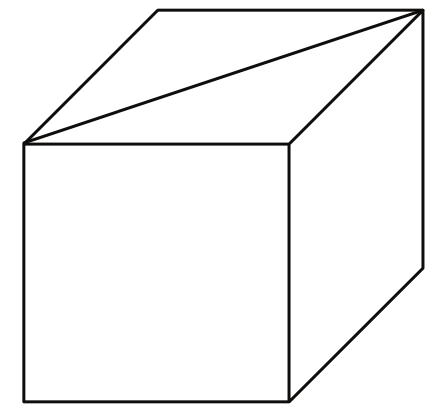
291. találat: Matematika középszintű érettségi, 2011. október, II. rész, 13. feladat
Témakör: *Algebra (gyökös egyenlet, trigonometrikus egyenlet, trigonometria) (Azonosító: mmk_201110_2r13f )

Oldja meg a valós számok halmazán az alábbi egyenleteket!

a) $ 5-x=\sqrt$

b) $\sin^2 x = 1+2 \cos x$

292. találat: Matematika középszintű érettségi, 2011. október, II. rész, 14. feladat
Témakör: *Statisztika (grafikon, valószínűségszámítás) (Azonosító: mmk_201110_2r14f )

Egy felmérés során két korcsoportban összesen 200 embert kérdeztek meg arról, hogy évente hány alkalommal járnak színházba. Közülük 120-an 40 évesnél fiatalabbak, 80 válaszadó pedig 40 éves vagy annál idősebb volt. Az eredményeket (százalékos megoszlásban) az alábbi diagram szemlélteti.

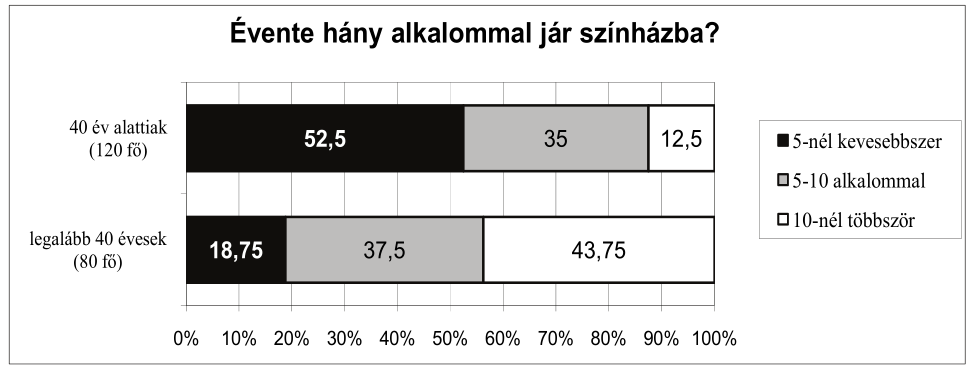
a) Hány legalább 40 éves ember adta azt a választ, hogy 5-nél kevesebbszer volt színházban?

b) A megkérdezettek hány százaléka jár évente legalább 5, de legfeljebb 10 alkalommal színházba?

c) A 200 ember közül véletlenszerűen kiválasztunk kettőt. Mekkora a valószínűsége annak, hogy közülük legfeljebb az egyik fiatalabb 40 évesnél? Válaszát három tizedesjegyre kerekítve adja meg!

293. találat: Matematika középszintű érettségi, 2011. október, II. rész, 15. feladat
Témakör: *Koordinátageometria (skalárszorzat, meredekség, hajlásszög) (Azonosító: mmk_201110_2r15f )

Adott két egyenes: $e: 5x-2y=-14,5$ ; $f: 2x+5y=14,5$ .

a) Határozza meg a két egyenes P metszéspontjának koordinátáit!

b) Igazolja, hogy az e és az f egyenesek egymásra merőlegesek!

c) Számítsa ki az e egyenes x tengellyel bezárt szögét!

294. találat: Matematika középszintű érettségi, 2011. október, II. rész, 16. feladat
Témakör: *Algebra (geometria, logaritmus) (Azonosító: mmk_201110_2r16f )

Újsághír: „Szeizmológusok számításai alapján a 2004. december 26-án Szumátra szigetének közelében kipattant földrengés a Richter-skála szerint 9,3-es erősségű volt; a rengést követő cunami (szökőár) halálos áldozatainak száma megközelítette a 300 ezret.”

A földrengés Richter-skála szerinti „erőssége” és a rengés középpontjában felszabaduló energia között fennálló összefüggés: $M=-4,42 + \dfrac \lg E$ .

Ebben a képletben E a földrengés középpontjában felszabaduló energia mérőszáma (joule-ban mérve), M pedig a földrengés erősségét megadó nem negatív szám a Richter- skálán.

a) A Nagasakira 1945-ben ledobott atombomba felrobbanásakor felszabaduló energia $ 1,344 \cdot 10^$ joule volt. A Richter-skála szerint mekkora erősségű az a földrengés, amelynek középpontjában ekkora energia szabadul fel?

b) A 2004. december 26-i szumátrai földrengésben mekkora volt a felszabadult energia?

c) A 2007-es chilei nagy földrengés erőssége a Richter-skála szerint 2-vel nagyobb volt, mint annak a kanadai földrengésnek az erőssége, amely ugyanebben az évben következett be. Hányszor akkora energia szabadult fel a chilei földrengésben, mint a kanadaiban?

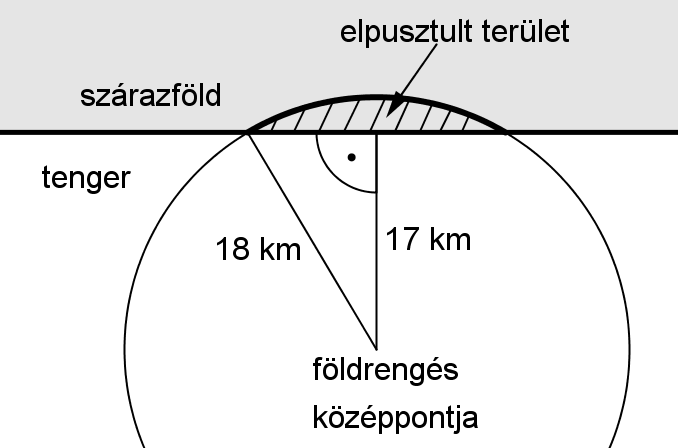
d) Az óceánban fekvő egyik szigeten a földrengést követően kialakuló szökőár egy körszelet alakú részt tarolt le. A körszeletet határoló körív középpontja a rengés középpontja, sugara pedig 18 km. A rengés középpontja a sziget partjától 17 km távolságban volt (lásd a felülnézeti ábrán). Mekkora a szárazföldön elpusztult rész területe egész négyzetkilométerre kerekítve?

295. találat: Matematika középszintű érettségi, 2011. október, II. rész, 17. feladat
Témakör: *Kombinatorika (számelmélet, oszthatóság) (Azonosító: mmk_201110_2r17f )

a) Hány olyan négy különböző számjegyből álló négyjegyű számot tudunk készíteni, amelynek mindegyik számjegye eleme az $\< 1; 2; 3; 4; 5; 6; 7\>$ halmaznak?

b) Hány 4-gyel osztható hétjegyű szám alkotható az 1, 2, 3, 4, 5 számjegyekből?

c) Hány olyan hatjegyű, hárommal osztható szám írható fel, amely csak az 1, 2, 3, 4, 5 számjegyeket tartalmazza, és e számjegyek mindegyike legalább egyszer előfordul benne?

296. találat: Matematika középszintű érettségi, 2011. október, II. rész, 18. feladat
Témakör: *Térgeometria (valószínűség, hasonlóság, binomiális eloszlás) (Azonosító: mmk_201110_2r18f )

Egy csonkakúp alakú tejfölös doboz méretei a következők: az alaplap átmérője 6 cm, a fedőlap átmérője 11 cm és az alkotója 8,5 cm.

a) Hány $cm^3$ tejföl kerül a dobozba, ha a gyárban a kisebbik körlapján álló dobozt magasságának 86%-áig töltik meg? Válaszát tíz $cm^3$ -re kerekítve adja meg!

b) A gyártás során a dobozok 3%-a megsérül, selejtes lesz. Az ellenőr a gyártott dobozok közül visszatevéssel 10 dobozt kiválaszt. Mennyi a valószínűsége annak, hogy a 10 doboz között lesz legalább egy selejtes? Válaszát két tizedesjegyre kerekítve adja meg!

297. találat: Matematika középszintű érettségi, 2012. május, I. rész, 1. feladat
Témakör: *Sorozatok (Azonosító: mmk_201205_1r01f )

Egy mértani sorozat első tagja 3, hányadosa (-2). Adja meg a sorozat első hat tagjának összegét!

298. találat: Matematika középszintű érettségi, 2012. május, I. rész, 2. feladat
Témakör: *Koordinátageometria (Azonosító: mmk_201205_1r02f )

Írja fel annak az e egyenesnek az egyenletét, amelyik párhuzamos a $ 2x-y=5$ egyenletű f egyenessel és áthalad a P(3; –2) ponton! Válaszát indokolja!

299. találat: Matematika középszintű érettségi, 2012. május, I. rész, 3. feladat
Témakör: *Függvények ( szélsőérték, másodfokú, parabola) (Azonosító: mmk_201205_1r03f )

Adott a valós számok halmazán értelmezett $f(x)=(x+2)^2+4$ függvény. Adja meg az f függvény minimumának helyét és értékét!

300. találat: Matematika középszintű érettségi, 2012. május, I. rész, 4. feladat
Témakör: *Logika ( kombinatorika, algebra) (Azonosító: mmk_201205_1r04f )

Döntse el, melyik állítás igaz, melyik hamis!

A) Hét tanulóból négyet ugyanannyiféleképpen lehet kiválasztani, mint hármat, ha a kiválasztás sorrendjétől mindkét esetben eltekintünk.

B) Van olyan x valós szám, amelyre igaz, hogy $\sqrt=-x$.

301. találat: Matematika középszintű érettségi, 2012. május, I. rész, 5. feladat
Témakör: *Algebra ( százalék) (Azonosító: mmk_201205_1r05f )

András 140 000 forintos fizetését megemelték $ 12 \%$-kal. Mennyi lett András fizetése az emelés után?

302. találat: Matematika középszintű érettségi, 2012. május, I. rész, 6. feladat
Témakör: *Algebra ( arány, szög) (Azonosító: mmk_201205_1r06f )

Határozza meg a radiánban megadott $\alpha = \dfrac<\pi>$ szög nagyságát fokban!

303. találat: Matematika középszintű érettségi, 2012. május, I. rész, 7. feladat
Témakör: *Koordinátageometria (Azonosító: mmk_201205_1r07f )

Adja meg az $(x+2)^2+y^2=9$ egyenletű kör K középpontjának koordinátáit és sugarának hosszát!

304. találat: Matematika középszintű érettségi, 2012. május, I. rész, 8. feladat
Témakör: *Algebra (Azonosító: mmk_201205_1r08f )

A testtömegindex kiszámítása során a vizsgált személy kilogrammban megadott tömegét osztják a méterben mért testmagasságának négyzetével. Számítsa ki Károly testtömegindexét, ha magassága 185 cm, tömege pedig 87 kg!

305. találat: Matematika középszintű érettségi, 2012. május, I. rész, 9. feladat
Témakör: *Valószínűségszámítás (Azonosító: mmk_201205_1r09f )

Egy piros és egy sárga szabályos dobókockát egyszerre feldobunk. Mennyi a valószínűsége annak, hogy a dobott számok összege pontosan 4 lesz? Válaszát indokolja!

306. találat: Matematika középszintű érettségi, 2012. május, I. rész, 10. feladat
Témakör: *Algebra ( logaritmus) (Azonosító: mmk_201205_1r10f )

Adja meg azokat az x valós számokat, melyekre teljesül: $\log_2 x^2=4$. Válaszát indokolja!

307. találat: Matematika középszintű érettségi, 2012. május, I. rész, 11. feladat
Témakör: *Algebra ( teljes négyzet, nevezetes azonosság) (Azonosító: mmk_201205_1r11f )

Egyszerűsítse a következő törtet: $\dfrac$, ahol $x \ne 3$ és $x \ne -3$.

308. találat: Matematika középszintű érettségi, 2012. május, I. rész, 12. feladat
Témakör: *Függvények ( trigonometria, szinusz, sin, koszinusz, cos) (Azonosító: mmk_201205_1r12f )

Az alább felsorolt, a valós számok halmazán értelmezett függvényeket közös koordinátarendszerben ábrázoljuk. A három függvény közül kettőnek a grafikonja megegyezik, a harmadik eltér tőlük. Melyik függvény grafikonja tér el a másik két függvény grafikonjától?

$A) \quad x\mapsto \dfrac \sin(2x) \qquad B) \quad x\mapsto \sin x \qquad C) \quad x\mapsto \cos \left( x-\dfrac<\pi>\right)$

309. találat: Matematika középszintű érettségi, 2012. május, II. rész, 13. feladat
Témakör: *Algebra ( exponenciális, egyenlet, törtes) (Azonosító: mmk_201205_2r13f )

Oldja meg az alábbi egyenleteket a valós számok halmazán!

b) $\dfrac-\dfrac=1$, ahol $x \ne 0$ és $x \ne -2$

310. találat: Matematika középszintű érettségi, 2012. május, II. rész, 14. feladat
Témakör: *Geometria ( terület, koszinusztétel, trapéz, hasonlóság) (Azonosító: mmk_201205_2r14f )

Az ABC hegyesszögű háromszögben BC = 14 cm, AC = 12 cm, a BCA szög nagysága pedig $ 40^$.

a) Számítsa ki a BC oldalhoz tartozó magasság hosszát!

b) Számítsa ki az AB oldal hosszát!

Válaszait cm-ben, egy tizedesjegyre kerekítve adja meg!

Az AB oldal felezőpontja legyen E, a BC oldal felezőpontja pedig legyen D.

c) Határozza meg az AEDC négyszög területét! Válaszát $cm^2$-ben, egy tizedesjegyre kerekítve adja meg!

311. találat: Matematika középszintű érettségi, 2012. május, II. rész, 15. feladat
Témakör: *Sorozatok (Azonosító: mmk_201205_2r15f )

Az újkori olimpiai játékok megrendezésére 1896 óta kerül sor, ebben az évben tartották az első (nyári) olimpiát Athénban. Azóta minden negyedik évben tartanak nyári olimpiát, és ezeket sorszámmal látják el. Három nyári olimpiát (az első és a második világháború miatt) nem tartottak meg, de ezek az elmaradt játékok is kaptak sorszámot.

a) Melyik évben tartották a 20. nyári olimpiai játékokat?

b) Számítsa ki, hogy a 2008-ban Pekingben tartott nyári olimpiának mi volt a sorszáma!

A nyári olimpiák szervezőinek egyik fő bevételi forrása a televíziós jogok értékesítéséből származó bevétel. Rendelkezésünkre állnak a következő adatok (millió dollárban számolva):

Eszter úgy véli, hogy a televíziós jogok értékesítéséből származó bevételek – a 20. olimpiától kezdve – az egymás utáni nyári olimpiákon egy számtani sorozat egymást követő tagjait alkotják. Marci szerint ugyanezek a számok egy mértani sorozat egymást követő tagjai. A saját modelljük alapján mindketten kiszámolják, hogy mennyi lehetett a televíziós jogok értékesítéséből származó bevétel a 27. nyári olimpián. Ezután megkeresik a tényleges adatot, amely egy internetes honlap szerint 1383 (millió dollár).

c) Számítsa ki, hogy Eszter vagy Marci becslése tér el kisebb mértékben a 27. nyári olimpia tényleges adatától!

312. találat: Matematika középszintű érettségi, 2012. május, II. rész, 16. feladat
Témakör: *Halmazok ( metszet, Venn-diagram, valószínűségszámítás) (Azonosító: mmk_201205_2r16f )

Tekintsük a következő halmazokat:

a) Töltse ki a táblázatot a minta alapján, majd a táblázat alapján írja be az 52, 78, 124, 216 számokat a halmazábra megfelelő tartományába!

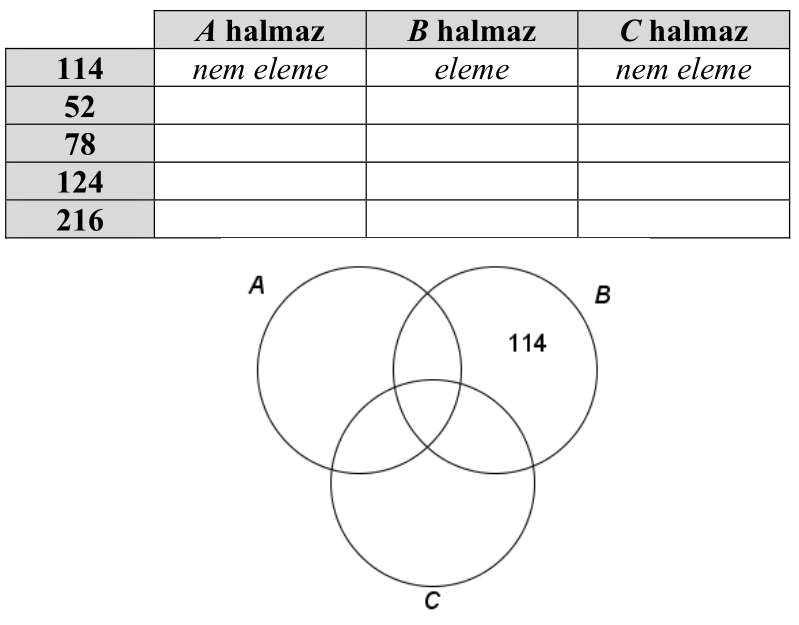
b) Határozza meg az $A \cap B \cap C$ halmaz elemszámát!
c) Számítsa ki annak valószínűségét, hogy az A halmazból egy elemet véletlenszerűen kiválasztva a kiválasztott szám nem eleme sem a B, sem a C halmaznak!

313. találat: Matematika középszintű érettségi, 2012. május, II. rész, 17. feladat
Témakör: *Statisztika ( kombinatorika) (Azonosító: mmk_201205_2r17f )

Az alábbi táblázat András és Bea érettségi érdemjegyeit mutatja.

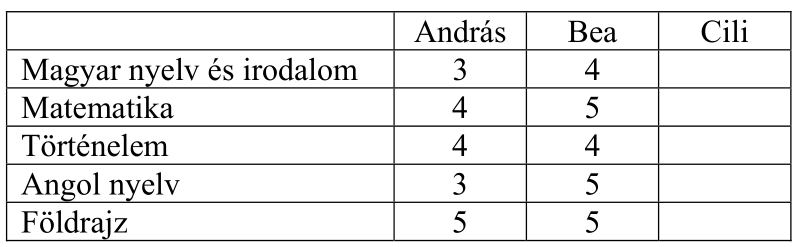
a) Számítsa ki András jegyeinek átlagát és szórását!

Cili érettségi eredményéről azt tudjuk, hogy jegyeinek átlaga András és Bea jegyeinek átlaga közé esik, továbbá Cili jegyeinek a szórása 0.

b) Töltse ki a táblázatot Cili jegyeivel!

Dávid is ebből az 5 tárgyból érettségizett, az 5 tárgy az ő bizonyítványában is a fenti sorrendben szerepel. Eredményeiről azt tudjuk, hogy jegyeinek mediánja 4, átlaga pedig 4,4 lett.

c) Határozza meg Dávid osztályzatait és azt, hogy hányféleképpen lehetne ezekkel az osztályzatokkal kitölteni az érettségi bizonyítványát!

Az ábra a 24 fős osztály érettségi eredményeinek megoszlását mutatja matematikából. Tudjuk, hogy jeles osztályzatot 4 tanuló ért el.

d) Az osztály tanulói közül hányan érettségiztek közepes eredménnyel matematikából?

314. találat: Matematika középszintű érettségi, 2012. május, II. rész, 18. feladat
Témakör: *Térgeometria ( kombinatorika, gráfok, Pitagorasz-tétel, koszinusztétel, ) (Azonosító: mmk_201205_2r18f )

a) Számítsa ki annak a szabályos négyoldalú gúlának a térfogatát, melynek minden éle 10 cm hosszú!

Térgeometriai feladatok megoldásában segíthet egy olyan készlet, melynek elemeiből (kilyuggatott kisméretű gömbökből és különböző hosszúságú műanyag pálcikákból) matematikai és kémiai modellek építhetők. Az ábrán egy kocka modellje látható.

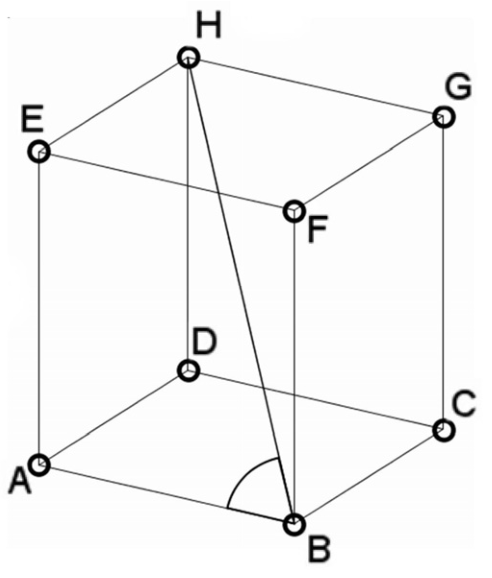
b) Számítsa ki az ABH szög nagyságát! (A test csúcsait tekintse pontoknak, az éleket pedig szakaszoknak!)

Anna egy molekulát modellezett a készlet segítségével, ehhez 7 gömböt és néhány pálcikát használt fel. Minden pálcika két gömböt kötött össze, és bármely két gömböt legfeljebb egy pálcika kötött össze. A modell elkészítése után feljegyezte, hogy hány pálcikát szúrt bele az egyes gömbökbe. A feljegyzett adatok: 6, 5, 3, 2, 2, 1, 1.

c) Mutassa meg, hogy Anna hibát követett el az adatok felírásában!

Anna is rájött, hogy hibázott. A helyes adatok: 6, 5, 3, 3, 2, 2, 1.

d) Hány pálcikát használt fel Anna a modell elkészítéséhez?

315. találat: Matematika középszintű érettségi, 2012. október, I. rész, 1. feladat
Témakör: *Sorozatok (Azonosító: mmk_201210_1r01f )

Az $\$ számtani sorozat első tagja és differenciája is 4. Adja meg a sorozat 26. tagját!

316. találat: Matematika középszintű érettségi, 2012. október, I. rész, 2. feladat
Témakör: *Halmazok ( metszet, különbség, unió) (Azonosító: mmk_201210_1r02f )

Az A és B halmazokról tudjuk, hogy $A \cup B =\$, $B\setminus A=\$ és $A \cap B =\$. Sorolja fel az A és a B halmaz elemeit!

317. találat: Matematika középszintű érettségi, 2012. október, I. rész, 3. feladat
Témakör: *Algebra ( négyzetgyök) (Azonosító: mmk_201210_1r03f )

Adja meg azt az x valós számot, melyre a következő egyenlőség teljesül! $\dfrac\cdot \sqrt=2$

318. találat: Matematika középszintű érettségi, 2012. október, I. rész, 4. feladat
Témakör: *Algebra ( geometria, arány) (Azonosító: mmk_201210_1r04f )

Egy középiskolának 480 tanulója van. A diákok egy része kollégiumban lakik, a többiek bejárók. A bejárók és a kollégisták nemek szerinti eloszlását mutatja a kördiagram. Adja meg a kollégista fiúk számát! Válaszát indokolja!

319. találat: Matematika középszintű érettségi, 2012. október, I. rész, 5. feladat
Témakör: *Kombinatorika (skatulyaelv) (Azonosító: mmk_201210_1r05f )

Egy érettségiző osztály félévi matematika osztályzatai között elégtelen nem volt, de az összes többi jegy előfordult. Legkevesebb hány tanulót kell kiválasztani közülük, hogy a kiválasztottak között biztosan legyen legalább kettő, akinek azonos volt félévkor a matematika osztályzata?

320. találat: Matematika középszintű érettségi, 2012. október, I. rész, 6. feladat
Témakör: *Algebra (százalék, törtrész) (Azonosító: mmk_201210_1r06f )

Egy szám $\dfrac$ részének a 20%-a 31. Melyik ez a szám? Válaszát indokolja!

321. találat: Matematika középszintű érettségi, 2012. október, I. rész, 7. feladat
Témakör: *Logika (függvények, számelmélet, geometria, statisztika) (Azonosító: mmk_201210_1r07f )

Döntse el, melyik állítás igaz, melyik hamis!

A) A valós számok halmazán értelmezett $f(x)=4$ hozzárendelési szabállyal megadott függvény grafikonja az x tengellyel párhuzamos egyenes.

B) Nincs két olyan prímszám, amelyek különbsége prímszám.

C) Az 1 cm sugarú kör kerületének cm-ben mért számértéke kétszer akkora, mint területének $cm^2$ -ben mért számértéke.

D) Ha egy adathalmaz átlaga 0, akkor a szórása is 0.

322. találat: Matematika középszintű érettségi, 2012. október, I. rész, 8. feladat
Témakör: *Kombinatorika (gráfok) (Azonosító: mmk_201210_1r08f )

Rajzoljon egy gráfot, melynek 5 csúcsa és 5 éle van, továbbá legalább az egyik csúcsának a fokszáma 3.

323. találat: Matematika középszintű érettségi, 2012. október, I. rész, 9. feladat
Témakör: *Függvények (trigonometria, szinusz, koszinusz) (Azonosító: mmk_201210_1r09f )

Adja meg az alábbi hozzárendelési szabályokkal megadott, a valós számok halmazán értelmezett függvények értékkészletét!

324. találat: Matematika középszintű érettségi, 2012. október, I. rész, 10. feladat
Témakör: *Geometria (vektor, paralelogramma-módszer) (Azonosító: mmk_201210_1r10f )

Az a és b vektorok $ 120^$-os szöget zárnak be egymással, mindkét vektor hossza 4 cm. Határozza meg az a + b vektor hosszát!

325. találat: Matematika középszintű érettségi, 2012. október, I. rész, 11. feladat
Témakör: *Geometria (sokszög) (Azonosító: mmk_201210_1r11f )

Számítsa ki a szabályos tizenkétszög egy belső szögének nagyságát! Válaszát indokolja!

326. találat: Matematika középszintű érettségi, 2012. október, I. rész, 12. feladat
Témakör: *Sorozatok (Azonosító: mmk_201210_1r12f )

A $\$ mértani sorozat hányadosa 2, első hat tagjának összege 94,5. Számítsa ki a sorozat első tagját! Válaszát indokolja!

327. találat: Matematika középszintű érettségi, 2012. október, II. rész, 13. feladat
Témakör: *Koordinátageometria (skaláris szorzat, koszinusztétel) (Azonosító: mmk_201210_2r13f )

Egy háromszög csúcsainak koordinátái: A(–2; –1), B(9; –3) és C(–3; 6).

a) Írja fel a BC oldal egyenesének egyenletét!

b) Számítsa ki a BC oldallal párhuzamos középvonal hosszát!

c) Számítsa ki a háromszögben a C csúcsnál lévő belső szög nagyságát!

328. találat: Matematika középszintű érettségi, 2012. október, II. rész, 14. feladat
Témakör: *Kombinatorika (valószínűségszámítás) (Azonosító: mmk_201210_2r14f )

Egy ajándéktárgyak készítésével foglalkozó kisiparos családi vállalkozása keretében zászlókat, kitűzőket is gyárt. Az ábrán az egyik általa készített kitűző stilizált képe látható. A kitűzőn lévő három mező kiszínezéséhez 5 szín (piros, kék, fehér, sárga, zöld) közül választhat. Egy mező kiszínezéséhez egy színt használ, és a különböző mezők lehetnek azonos színűek is.

a) Hányféle háromszínű kitűzőt készíthet a kisiparos?

b) Hányféle kétszínű kitűző készíthető?

A kisiparos elkészíti az összes lehetséges különböző (egy-, két- és háromszínű) kitűzőt egy-egy példányban, és véletlenszerűen kiválaszt közülük egyet.

c) Mennyi annak a valószínűsége, hogy olyan kitűzőt választ, amelyen az egyik mező kék, egy másik sárga, a harmadik pedig zöld színű?

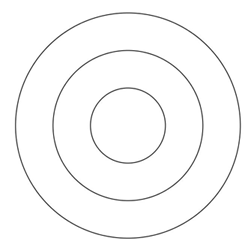
329. találat: Matematika középszintű érettségi, 2012. október, II. rész, 15. feladat
Témakör: *Függvények (algebra, lineáris, másodfokú) (Azonosító: mmk_201210_2r15f )

Legyenek f és g a valós számok halmazán értelmezett függvények, továbbá:

a) Számítsa ki az alábbi táblázatok hiányzó értékeit!

b) Adja meg a g függvény értékkészletét!
c) Oldja meg az $ 5x+5,25 > x^2+2x+3,5$ egyenlőtlenséget a valós számok halmazán!

330. találat: Matematika középszintű érettségi, 2012. október, II. rész, 16. feladat
Témakör: *Algebra (szöveges feladat, százalék) (Azonosító: mmk_201210_2r16f )

Stefi mobiltelefon-költségeinek fedezésére feltöltőkártyát szokott vásárolni. A mobiltársaság ebben az esetben sem előfizetési díjat, sem hívásonkénti kapcsolási díjat nem számol fel. Csúcsidőben a percdíj 25 forinttal drágább, mint csúcsidőn kívül. Stefi az elmúlt négy hétben összesen 2 órát telefonált és 4000 Ft-ot használt fel kártyája egyenlegéből úgy, hogy ugyanannyi pénzt költött csúcsidőn belüli, mint csúcsidőn kívüli beszélgetésekre.

a) Hány percet beszélt Stefi mobiltelefonján csúcsidőben az elmúlt négy hétben?

A mobiltársaság Telint néven új mobilinternet csomagot vezet be a piacra január elsején. Januárban 10000 új előfizetőt várnak, majd ezután minden hónapban az előző havinál 7,5%-kal több új előfizetőre számítanak. Abban a hónapban, amikor az adott havi új előfizetők száma eléri a 20000-et, a társaság változtatni szeretne a Telint csomag árán.

b) Számítsa ki, hogy a tervek alapján melyik hónapban éri el a Telint csomag egyhavi új előfizetőinek a száma a 20000-et!

331. találat: Matematika középszintű érettségi, 2012. október, II. rész, 17. feladat
Témakör: *Térgeometria (hasonlóság) (Azonosító: mmk_201210_2r17f )

Egy szabályos négyoldalú (négyzet alapú) gúla alapéle 12 cm, oldallapjai $ 60^$-os szöget zárnak be az alaplap síkjával.

a) Számítsa ki a gúla felszínét ($cm^2$-ben) és térfogatát ($cm^3$-ben)! Válaszait egészre kerekítve adja meg!

A gúlát két részre osztjuk egy az alaplappal párhuzamos síkkal, amely a gúla magasságát a csúcstól távolabbi harmadoló pontban metszi.

b) Mekkora a keletkező gúla és csonkagúla térfogatának aránya? Válaszát egész számok hányadosaként adja meg!

c) Számítsa ki a keletkező csonkagúla felszínét $cm^2$-ben!

332. találat: Matematika középszintű érettségi, 2012. október, II. rész, 18. feladat
Témakör: *Statisztika (valószínűségszámítás) (Azonosító: mmk_201210_2r18f )

Az egyik világbajnokságon részt vevő magyar női vízilabdacsapat 13 tagjának életkor szerinti megoszlását mutatja az alábbi táblázat.

a) Számítsa ki a csapat átlagéletkorát!

Jelölje A azt az eseményt, hogy a csapatból 7 játékost véletlenszerűen kiválasztva, a kiválasztottak között legfeljebb egy olyan van, aki 20 évnél fiatalabb.

b) Számítsa ki az A esemény valószínűségét! A világbajnokság egyik mérkőzésén a magyar kezdőcsapat 6 mezőnyjátékosáról a következőket tudjuk:

• a legidősebb és a legfiatalabb játékos életkorának különbsége 12 év,

• a játékosok életkorának egyetlen módusza 22 év,

• a hat játékos életkorának mediánja 23 év,

• a hat játékos életkorának átlaga 24 év.

c) Adja meg a kezdőcsapat hat mezőnyjátékosának életkorát!

333. találat: Matematika középszintű érettségi, 2013. május, I. rész, 1. feladat
Témakör: *Halmazok ( unió, különbség) (Azonosító: mmk_201305_1r01f )

Az A és B halmazokról tudjuk, hogy $A \cup B = \$ és $B \setminus A =\$. Elemeinek felsorolásával adja meg az A halmazt!

334. találat: Matematika középszintű érettségi, 2013. május, I. rész, 2. feladat
Témakör: *Statisztika ( átlag) (Azonosító: mmk_201305_1r02f )

Egy kis cégnél nyolcan dolgoznak: hat beosztott és két főnök. A főnökök átlagos havi jövedelme 190 000 Ft, a beosztottaké 150 000 Ft. Hány forint a cég nyolc dolgozójának átlagos havi jövedelme?

335. találat: Matematika középszintű érettségi, 2013. május, I. rész, 3. feladat
Témakör: *Geometria ( arány, algebra) (Azonosító: mmk_201305_1r03f )

Az ábra egy sütemény alapanyagköltségeinek megoszlását mutatja. Számítsa ki a „vaj” feliratú körcikk középponti szögének nagyságát fokban! Válaszát indokolja!

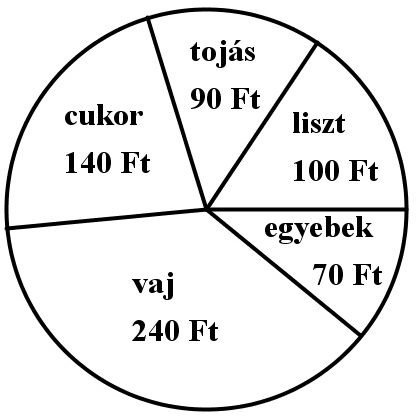
336. találat: Matematika középszintű érettségi, 2013. május, I. rész, 4. feladat
Témakör: *Függvények ( abszolútérték) (Azonosító: mmk_201305_1r04f )

Az alábbi hozzárendelési utasítással megadott, a valós számok halmazán értelmezett függvények közül kettőnek egy-egy részletét ábrázoltuk. Adja meg a grafikonokhoz tartozó hozzárendelési utasítások betűjelét!

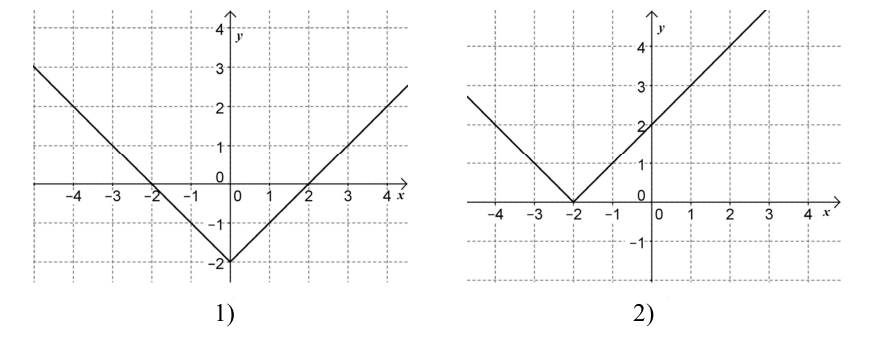
$A) \ x\mapsto |x+2| \qquad B) \ x\mapsto |x-2| \qquad C) \ x\mapsto |x|-2 \qquad D) \ x\mapsto |x|+2$

337. találat: Matematika középszintű érettségi, 2013. május, I. rész, 5. feladat
Témakör: *Geometria ( trigonometria, szögfüggvény) (Azonosító: mmk_201305_1r05f )

A vízszintessel 6,5°-ot bezáró egyenes út végpontja 124 méterrel magasabban van, mint a kiindulópontja. Hány méter hosszú az út? Válaszát indokolja!

338. találat: Matematika középszintű érettségi, 2013. május, I. rész, 6. feladat
Témakör: *Koordinátageometria (Azonosító: mmk_201305_1r06f )

Adja meg a 2x + y = 4 egyenletű egyenes és az x tengely M metszéspontjának a koordinátáit, valamint az egyenes meredekségét!

339. találat: Matematika középszintű érettségi, 2013. május, I. rész, 7. feladat
Témakör: *Függvények ( parabola) (Azonosító: mmk_201305_1r07f )

Adja meg az $x\mapsto x^2+10x+21 \quad (x \in \mathbb)$ másodfokú függvény minimumhelyét és minimumának értékét! Válaszát indokolja!

340. találat: Matematika középszintű érettségi, 2013. május, I. rész, 8. feladat
Témakör: *Logika ( statisztika, geometria, algebra) (Azonosító: mmk_201305_1r08f )

Adja meg a következő állítások logikai értékét (igaz vagy hamis)!

A) A adathalmaz szórása 4.

B) Ha egy sokszög minden oldala egyenlő hosszú, akkor a sokszög szabályos.

C) A 4 és a 9 mértani közepe 6.

341. találat: Matematika középszintű érettségi, 2013. május, I. rész, 9. feladat
Témakör: *Térgeometria ( hasonlóság, arány) (Azonosító: mmk_201305_1r09f )

Két gömb sugarának aránya 2 : 1. A nagyobb gömb térfogata k-szorosa a kisebb gömb térfogatának. Adja meg k értékét!

342. találat: Matematika középszintű érettségi, 2013. május, I. rész, 10. feladat
Témakör: *Kombinatorika ( permutáció) (Azonosító: mmk_201305_1r10f )

Egy futóverseny döntőjébe hat versenyző jutott, jelöljük őket A, B, C, D, E és F betűvel. A cél előtt pár méterrel már látható, hogy C biztosan utolsó lesz, továbbá az is biztos, hogy B és D osztozik majd az első két helyen. Hányféleképpen alakulhat a hat versenyző sorrendje a célban, ha nincs holtverseny? Válaszát indokolja!

343. találat: Matematika középszintű érettségi, 2013. május, I. rész, 11. feladat
Témakör: *Statisztika (Azonosító: mmk_201305_1r11f )

Réka év végi bizonyítványában a következő osztályzatok szerepelnek: 4; 2; 3; 5; 5; 4; 5; 5; 4. Adja meg Réka osztályzatainak móduszát és mediánját!

344. találat: Matematika középszintű érettségi, 2013. május, I. rész, 12. feladat
Témakör: *Valószínűségszámítás ( számelmélet) (Azonosító: mmk_201305_1r12f )

Adja meg annak valószínűségét, hogy a 7, 8, 9, 10, 11, 12, 13, 14 számok közül egyet véletlenszerűen kiválasztva a kiválasztott szám prím!

345. találat: Matematika középszintű érettségi, 2013. május, II. rész, 13. feladat
Témakör: *Sorozatok (Azonosító: mmk_201305_2r13f )

a) Egy számtani sorozat első tagja 2, első hét tagjának összege 45,5. Adja meg a sorozat hatodik tagját!

b) Egy mértani sorozat első tagja 5, második és harmadik tagjának összege 10. Adja meg a sorozat első hét tagjának az összegét!

346. találat: Matematika középszintű érettségi, 2013. május, II. rész, 14. feladat
Témakör: *Koordinátageometria (skaláris szorzat, skalárszorzat, koszinusztétel) (Azonosító: mmk_201305_2r14f )

a) Írja fel a háromszög P csúcsához tartozó súlyvonal egyenesének egyenletét!

b) Számítsa ki a háromszög P csúcsnál lévő belső szögének nagyságát!

347. találat: Matematika középszintű érettségi, 2013. május, II. rész, 15. feladat
Témakör: *Algebra (százalék) (Azonosító: mmk_201305_2r15f )

A munkavállaló nettó munkabérét a bruttó béréből számítják ki levonások és jóváírások alkalmazásával. Kovács úr bruttó bére 2010 áprilisában 200 000 forint volt. A 2010-ben érvényes szabályok alapján különböző járulékokra ennek a bruttó bérnek összesen 17%-át vonták le. Ezen felül a bruttó bérből személyi jövedelemadót is levontak, ez a bruttó bér 127%-ának a 17%-a volt. A levonások után megmaradó összeghez hozzáadtak 15 100 forintot adójóváírásként. Az így kapott érték volt Kovács úr nettó bére az adott hónapban.

a) Számítsa ki, hogy Kovács úr bruttó bérének hány százaléka volt a nettó bére az adott hónapban!

Szabó úr nettó bére 2010 áprilisában 173 015 forint volt. Szabó úr fizetésénél a levonásokat ugyanazzal az eljárással számították ki, mint Kovács úr esetében, de ebben a hónapban Szabó úr csak 5980 forint adójóváírást kapott.

b) Hány forint volt Szabó úr bruttó bére az adott hónapban?

348. találat: Matematika középszintű érettségi, 2013. május, II. rész, 16. feladat
Témakör: *Kombinatorika (gráfok, valószínűségszámítás) (Azonosító: mmk_201305_2r16f )

Egy iskola asztalitenisz bajnokságán hat tanuló vesz részt. Mindenki mindenkivel egy mérkőzést játszik. Eddig Andi egy mérkőzést játszott, Barnabás és Csaba kettőt-kettőt, Dani hármat, Enikő és Feri négyet-négyet.

a) Rajzolja le az eddig lejátszott mérkőzések egy lehetséges gráfját!

b) Lehetséges-e, hogy Andi az eddig lejátszott egyetlen mérkőzését Barnabással játszotta? (Igen válasz esetén rajzoljon egy megfelelő gráfot; nem válasz esetén válaszát részletesen indokolja!)

c) Számítsa ki annak a valószínűségét, hogy a hat játékos közül kettőt véletlenszerűen kiválasztva, ők eddig még nem játszották le az egymás elleni mérkőzésüket!

349. találat: Matematika középszintű érettségi, 2013. május, II. rész, 17. feladat
Témakör: *Algebra (törtes, exponenciális, trigonometrikus) (Azonosító: mmk_201305_2r17f )

a) Oldja meg a valós számok halmazán az $\dfrac\geq 0$ egyenlőtlenséget!

b) Adja meg az x négy tizedesjegyre kerekített értékét, ha $ 4\cdot 3^x+3^x=20$.

c) Oldja meg a $ 2 \cos^2x+3 \cosx-2=0$ egyenletet a $[-\pi; \pi]$ alaphalmazon!

350. találat: Matematika középszintű érettségi, 2013. május, II. rész, 18. feladat
Témakör: *Térgeometria (valószínűségszámítás) (Azonosító: mmk_201305_2r18f )

Tekintsünk két egybevágó, szabályos négyoldalú (négyzet alapú) gúlát, melyek alapélei 2 cm hosszúak, oldalélei pedig 3 cm-esek. A két gúlát alaplapjuknál fogva összeragasztjuk (az alaplapok teljesen fedik egymást), így az ábrán látható testet kapjuk.

a) Számítsa ki ennek a testnek a felszínét (cm 2 -ben) és a térfogatát (cm 3 -ben)! Válaszait egy tizedesjegyre kerekítve adja meg!

A test lapjait 1-től 8-ig megszámozzuk, így egy „dobó-oktaédert” kapunk, amely minden oldallapjára egyforma valószínűséggel esik. Egy ilyen test esetében is van egy felső lap, az ezen lévő számot tekintjük a dobás kimenetelének. (Az ábrán látható „dobóoktaéderrel” 8-ast dobtunk.)

b) Határozza meg annak a valószínűségét, hogy ezzel a „dobóoktaéderrel” egymás után négyszer dobva, legalább három esetben 5-nél nagyobb számot dobunk!

351. találat: Matematika középszintű érettségi, 2013. október, I. rész, 1. feladat
Témakör: *Halmazok ( különbség) (Azonosító: mmk_201310_1r01f )

Az A halmaz elemei a (−5)-nél nagyobb, de 2-nél kisebb egész számok. B a pozitív egész számok halmaza. Elemeinek felsorolásával adja meg az A\B halmazt!

352. találat: Matematika középszintű érettségi, 2013. október, I. rész, 2. feladat
Témakör: *Függvények (abszolútérték, algebra, egyenlet) (Azonosító: mmk_201310_1r02f )

Adott a valós számok halmazán értelmezett $f(x)=|x-4|$ függvény. Mely x értékek esetén lesz f(x)=6 ?

353. találat: Matematika középszintű érettségi, 2013. október, I. rész, 3. feladat
Témakör: *Algebra (trigonometria) (Azonosító: mmk_201310_1r03f )

Oldja meg a $[-\pi; \pi]$ zárt intervallumon a $\cos x =\dfrac$ egyenletet!

354. találat: Matematika középszintű érettségi, 2013. október, I. rész, 4. feladat
Témakör: *Számelmélet (logika, LNKO) (Azonosító: mmk_201310_1r04f )

Adja meg az alábbi állítások logikai értékét (igaz vagy hamis)!

A) Két különböző pozitív egész szám legnagyobb közös osztója mindig kisebb mindkét számnál.

B) Két különböző pozitív egész szám legnagyobb közös osztója mindig osztója a két szám összegének.

C) Két különböző pozitív egész szám legnagyobb közös osztója nem lehet 1.

355. találat: Matematika középszintű érettségi, 2013. október, I. rész, 5. feladat
Témakör: *Algebra (szöveges egyenlet, százalék) (Azonosító: mmk_201310_1r05f )

Egy országban egy választáson a szavazókorú népesség 63,5%-a vett részt. A győztes pártra a résztvevők 43,6%-a szavazott. Hány fős a szavazókorú népesség, ha a győztes pártra 4 152 900 fő szavazott? Válaszát indokolja!

356. találat: Matematika középszintű érettségi, 2013. október, I. rész, 6. feladat
Témakör: *Függvények (lineáris, egyenes) (Azonosító: mmk_201310_1r06f )

Az ábrán az $x\mapsto m\cdot x+b$ lineáris függvény grafikonjának egy részlete látható. Határozza meg m és b értékét!

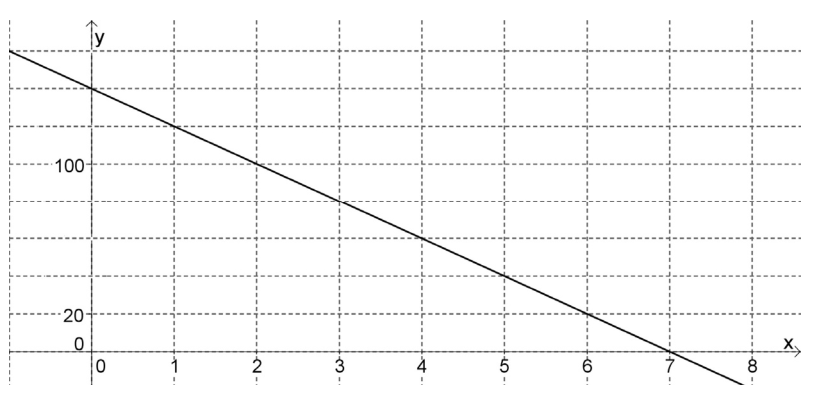
357. találat: Matematika középszintű érettségi, 2013. október, I. rész, 7. feladat
Témakör: *Geometria (egybevágóság) (Azonosító: mmk_201310_1r07f )

Adja meg, hogy az alábbi geometriai transzformációk közül melyek viszik át önmagába az ábrán látható, háromszög alakú (sugárveszélyt jelző) táblát!

A) 60°-os elforgatás a tábla középpontja körül.

B) 120°-os elforgatás a tábla középpontja körül.

C) Középpontos tükrözés a tábla középpontjára.

D) Tengelyes tükrözés a tábla középpontján és a tábla egyik csúcsán átmenő tengelyre.

358. találat: Matematika középszintű érettségi, 2013. október, I. rész, 8. feladat
Témakör: *Sorozatok (algebra, egyenletrendszer, lineáris) (Azonosító: mmk_201310_1r08f )

Egy számtani sorozat hatodik tagja 15, kilencedik tagja 0. Számítsa ki a sorozat első tagját! Válaszát indokolja!

359. találat: Matematika középszintű érettségi, 2013. október, I. rész, 9. feladat
Témakör: *Kombinatorika (gráf) (Azonosító: mmk_201310_1r09f )

Rajzoljon egy olyan 5 csúcsú gráfot, melyben a csúcsok fokszámának összege 12.

360. találat: Matematika középszintű érettségi, 2013. október, I. rész, 10. feladat
Témakör: *Függvények (exponenciális) (Azonosító: mmk_201310_1r10f )

Az ábrán az $f:[-2;1]\rightarrow \mathbb; f(x)=a^x$ függvény grafikonja látható.

a) Adja meg az f függvény értékkészletét! b) Határozza meg az a szám értékét!

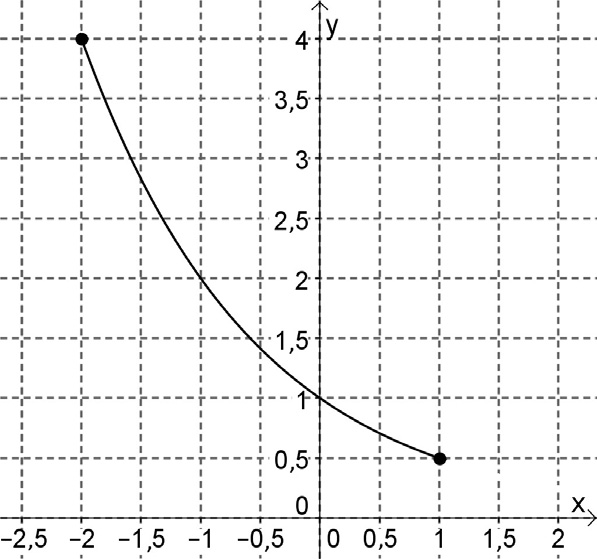
361. találat: Matematika középszintű érettségi, 2013. október, I. rész, 11. feladat
Témakör: *Valószínűségszámítás (számelmélet, osztó) (Azonosító: mmk_201310_1r11f )

Adja meg annak az eseménynek a valószínűségét, hogy egy szabályos dobókockával egyszer dobva a dobott szám osztója a 60-nak! Válaszát indokolja!

362. találat: Matematika középszintű érettségi, 2013. október, I. rész, 12. feladat
Témakör: *Algebra (arány, körcikk) (Azonosító: mmk_201310_1r12f )

Egy gyümölcsárus háromféle almát kínál a piacon. A teljes készletről kördiagramot készítettünk. Írja a táblázat megfelelő mezőibe a hiányzó adatokat!

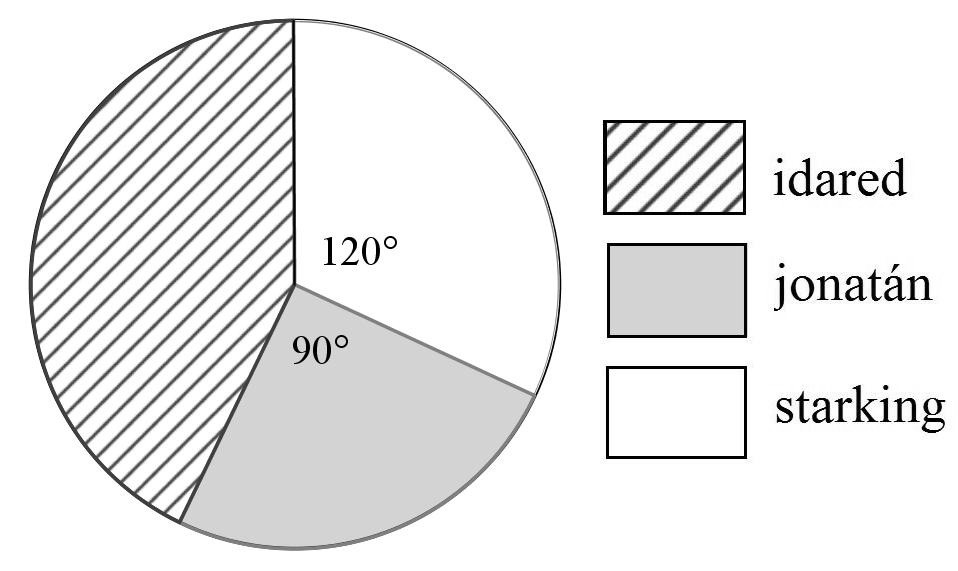
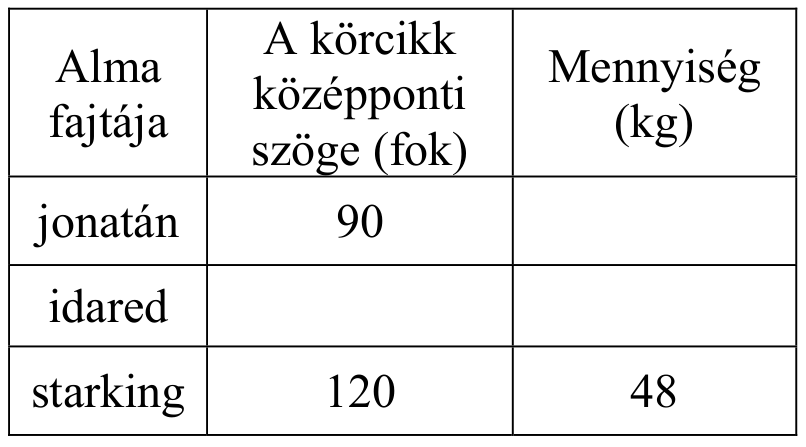
363. találat: Matematika középszintű érettségi, 2013. október, II. rész, 13. feladat
Témakör: *Algebra (gyökös, lineáris) (Azonosító: mmk_201310_2r13f )

a) Oldja meg a valós számok halmazán a következő egyenletet!

b) Oldja meg az alábbi egyenletrendszert, ahol x és y valós számot jelöl!

364. találat: Matematika középszintű érettségi, 2013. október, II. rész, 14. feladat
Témakör: *Geometria (súlyvonal, koszinusztétel, szinusztétel) (Azonosító: mmk_201310_2r14f )

Az ábrán látható ABC háromszögben a D pont felezi az AB oldalt. A háromszögben ismert: AB = 48 mm, CD = 41 mm, $\delta=47^$.

a) Számítsa ki az ABC háromszög területét!

b) Számítással igazolja, hogy (egész milliméterre kerekítve) a háromszög BC oldalának hossza 60 mm!

c) Számítsa ki a háromszög B csúcsánál lévő belső szög nagyságát!

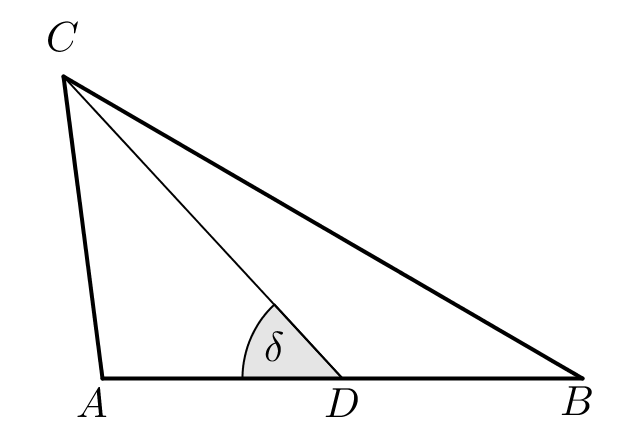
365. találat: Matematika középszintű érettségi, 2013. október, II. rész, 15. feladat
Témakör: *Halmazok (Venn-diagram, statisztika, logika) (Azonosító: mmk_201310_2r15f )

Egy végzős osztály diákjai projektmunka keretében különböző statisztikai felméréseket készítettek az iskola tanulóinak körében.

a) Éva 150 diákot kérdezett meg otthonuk felszereltségéről. Felméréséből kiderült, hogy a megkérdezettek közül kétszer annyian rendelkeznek mikrohullámú sütővel, mint mosogatógéppel. Azt is megtudta, hogy 63-an mindkét géppel, 9-en egyik géppel sem rendelkeznek. A megkérdezettek hány százalékának nincs otthon mikrohullámú sütője?

b) Jóska a saját felmérésében 200 diákot kérdezett meg arról, hogy hány számítógépük van a háztartásban. A válaszokat a következő táblázatban összesítette:

A számítógépek szá- ma a háztartásban	Gyakoriság
0	3
1	94
2	98
3	14

Jóska felmérése alapján töltse ki az alábbi táblázatot az egy háztartásban található számítógépek számáról!

A számítógépek számának átlaga

A számítógépek számának mediánja

A számítógépek számának módusza

c) Tamás a saját felmérése alapján a következőt állítja: Minden háztartásban van televízió. Az alábbi négy állítás közül válassza ki azt a kettőt, amely Tamás állításának tagadása!

A) Semelyik háztartásban nincs televízió.

B) Van olyan háztartás, ahol van televízió.

C) Van olyan háztartás, ahol nincs televízió.

D) Nem minden háztartásban van televízió.

366. találat: Matematika középszintű érettségi, 2013. október, II. rész, 16. feladat
Témakör: *Függvények (algebra, exponenciális, térgeometria, sorozat, mértani, logaritmus) (Azonosító: mmk_201310_2r16f )

A kólibaktérium (hengeres) pálcika alakú, hossza átlagosan 2 mikrométer $(2\cdot10^ m)$, átmérője 0,5 mikrométer $(5\cdot10^ m)$ .

a) Számítsa ki egy 2 mikrométer magas és 0,5 mikrométer átmérőjű forgáshenger térfogatát és felszínét! Számításainak eredményét m 3 -ben, illetve m 2 -ben, normálalakban adja meg!

Ideális laboratóriumi körülmények között a kólibaktériumok gyorsan és folyamatosan osztódnak, számuk 15 percenként megduplázódik. Egy tápoldat kezdetben megközelítőleg 3 millió kólibaktériumot tartalmaz.

b) Hány baktérium lesz a tápoldatban 1,5 óra elteltével?

A baktériumok számát a tápoldatban t perc elteltével a $B(t)=9000000 \cdot 2^>$ összefüggés adja meg.

c) Hány perc alatt éri el a kólibaktériumok száma a tápoldatban a 600 milliót? Válaszát egészre kerekítve adja meg!

367. találat: Matematika középszintű érettségi, 2013. október, II. rész, 17. feladat
Témakör: *Koordinátageometria (Thalesz) (Azonosító: mmk_201310_2r17f )

Adott a koordináta-rendszerben két pont: A(1; –3) és B(7; –1).

a) Írja fel az A és B pontokra illeszkedő e egyenes egyenletét!

b) Számítással igazolja, hogy az A és a B pont is illeszkedik az $x^2+y^2-6x-2y=10$ egyenletű k körre, és számítsa ki az AB húr hosszát!

Az f egyenesről tudjuk, hogy illeszkedik az A pontra és merőleges az AB szakaszra.

c) Számítsa ki a k kör és az f egyenes (A-tól különböző) metszéspontjának koordinátáit!

368. találat: Matematika középszintű érettségi, 2013. október, II. rész, 18. feladat
Témakör: *Valószínűségszámítás (kombinatorika) (Azonosító: mmk_201310_2r18f )

a) Egy memóriajáték 30 olyan egyforma méretű lapból áll, melyek egyik oldalán egy-egy egész szám áll az 1, 2, 3, … 14, 15 számok közül. Mindegyik szám pontosan két lapon szerepel. A lapok másik oldala (a hátoldala) teljesen azonos mintázatú. A 30 lapot összekeverjük. A játék kezdetén a lapokat az asztalra helyezzük egymás mellé, hátoldalukkal felfelé fordítva, így a számok nem látszanak. Számítsa ki annak a valószínűségét, hogy a játék kezdetén két lapot véletlenszerűen kiválasztva a lapokon álló számok megegyeznek!

b) Egy dominókészlet azonos méretű kövekből áll. Minden dominókő egyik oldala egy vonallal két részre van osztva. Az egyes részeken elhelyezett pöttyök száma 0-tól 6-ig bármi lehet. Minden lehetséges párosításnak léteznie kell, de két egyforma kő nem lehet egy készletben. Az ábrán két kő látható: a 4-4-es és a 0-5-ös (vagy 5-0-ás). Hány kőből áll egy dominókészlet?

c) A „Ki nevet a végén?” nevű társasjátékban egy játékos akkor indulhat el a pályán, amikor egy szabályos dobókockával 6-ost dob. Számítsa ki annak a valószínűségét, hogy valaki pontosan a harmadik dobására indulhat el a pályán!

369. találat: Matematika középszintű érettségi, 2014. május, I. rész, 1. feladat
Témakör: *Halmazok ( metszet, különbség) (Azonosító: mmk_201405_1r01f )

Legyen A halmaz a 8-nál nem nagyobb pozitív egész számok halmaza, B pedig a 3-mal osztható egyjegyű pozitív egész számok halmaza. Elemeinek felsorolásával adja meg az A, a B, az $A \cap B$ és az $A \setminus B$ halmazt!

370. találat: Matematika középszintű érettségi, 2014. május, I. rész, 2. feladat
Témakör: *Algebra ( százalék) (Azonosító: mmk_201405_1r02f )

Egy konzerv tömege a konzervdobozzal együtt 750 gramm. A konzervdoboz tömege a teljes tömeg $ 12\%$-a. Hány gramm a konzerv tartalma?

371. találat: Matematika középszintű érettségi, 2014. május, I. rész, 3. feladat
Témakör: *Algebra ( másodfokú) (Azonosító: mmk_201405_1r03f )

Oldja meg a következő egyenletet a valós számok halmazán:$(x-3)^2+2x=14$. Válaszát indokolja!

372. találat: Matematika középszintű érettségi, 2014. május, I. rész, 4. feladat
Témakör: *Függvények ( másodfokú, lineáris) (Azonosító: mmk_201405_1r04f )

Válassza ki az f függvény hozzárendelési szabályát az A, B, C, D lehetőségek közül úgy, hogy az megfeleljen az alábbi értéktáblázatnak:

x	-2	0	2
f(x)	-4	0	-4

$\textbf f(x)=2x \qquad \textbf f(x)=x^2 \qquad \textbf f(x)=-2x \qquad \textbf f(x)=-x^2 $

373. találat: Matematika középszintű érettségi, 2014. május, I. rész, 5. feladat
Témakör: *Halmazok (Azonosító: mmk_201405_1r05f )

Egy osztályban 25-en tanulnak angolul, 17-en tanulnak németül. E két nyelv közül legalább az egyiket mindenki tanulja. Hányan tanulják mindkét nyelvet, ha az osztály létszáma 30?

374. találat: Matematika középszintű érettségi, 2014. május, I. rész, 6. feladat
Témakör: *Algebra ( százalék) (Azonosító: mmk_201405_1r06f )

Egy termék árát az egyik hónapban $ 20\%$-kal, majd a következő hónapban újabb $ 20\%$-kal megemelték. A két áremelés együttesen hány százalékos áremelésnek felel meg? Válaszát indokolja!

375. találat: Matematika középszintű érettségi, 2014. május, I. rész, 7. feladat
Témakör: *Számelmélet ( oszthatóság) (Azonosító: mmk_201405_1r07f )

Melyik számjegy állhat a $\overline$ ötjegyű számban az X helyén, ha a szám osztható 3-mal? Válaszát indokolja!

376. találat: Matematika középszintű érettségi, 2014. május, I. rész, 8. feladat
Témakör: *Függvények ( abszolútérték) (Azonosító: mmk_201405_1r08f )

Az ábrán a [–1; 5] intervallumon értelmezett függvény grafikonja látható. Válassza ki a felsoroltakból a függvény hozzárendelési szabályát!

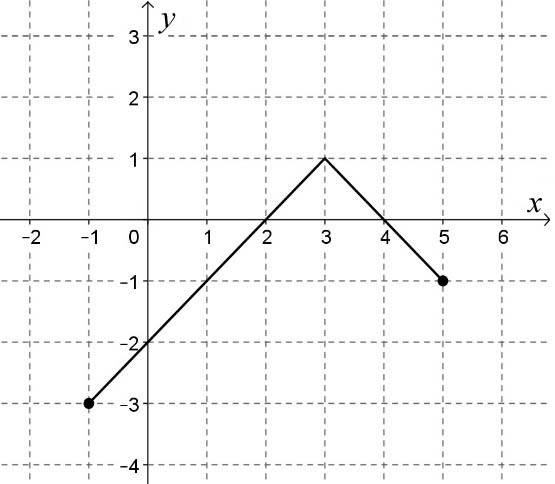
377. találat: Matematika középszintű érettségi, 2014. május, I. rész, 9. feladat
Témakör: *Algebra ( logaritmus) (Azonosító: mmk_201405_1r09f )

Adja meg az x értékét, ha $\log_2(x+1)=5$ .

378. találat: Matematika középszintű érettségi, 2014. május, I. rész, 10. feladat
Témakör: *Kombinatorika ( gráfok) (Azonosító: mmk_201405_1r10f )

Egy irodai számítógép-hálózat hat gépből áll. Mindegyik gép ezek közül három másikkal van közvetlenül összekötve. Rajzoljon egy olyan gráfot, amely ezt a hálózatot szemlélteti!

379. találat: Matematika középszintű érettségi, 2014. május, I. rész, 11. feladat
Témakör: *Geometria ( Thalesz-tétel, Pitagorasz-tétel) (Azonosító: mmk_201405_1r11f )

Egy téglalap szomszédos oldalainak hossza 4,2 cm és 5,6 cm. Mekkora a téglalap körülírt körének sugara? Válaszát indokolja!

380. találat: Matematika középszintű érettségi, 2014. május, I. rész, 12. feladat
Témakör: *Valószínűségszámítás (Azonosító: mmk_201405_1r12f )

Egy kalapban 3 piros, 4 kék és 5 zöld golyó van. Találomra kihúzunk a kalapból egy golyót. Adja meg annak valószínűségét, hogy a kihúzott golyó nem piros!

381. találat: Matematika középszintű érettségi, 2014. október, I. rész, 1. feladat
Témakör: *Koordinátageometria (Azonosító: mmk_201410_1r01f )

Írja fel annak az egyenesnek az egyenletét, amely áthalad az (1; –3) ponton, és egyik normálvektora a (8; 1) vektor!

382. találat: Matematika középszintű érettségi, 2014. október, I. rész, 2. feladat
Témakör: *Algebra (polinom, azonosság) (Azonosító: mmk_201410_1r02f )

Végezze el a következő műveleteket, és vonja össze az egynemű kifejezéseket! A számítás menetét részletezze!

383. találat: Matematika középszintű érettségi, 2014. október, I. rész, 3. feladat
Témakör: *Függvény (másodfokú) (Azonosító: mmk_201410_1r03f )

Adott a valós számok halmazán értelmezett $x\mapsto -(x-5)^2+4$ függvény. Melyik ábrán látható e függvény grafikonjának egy részlete?

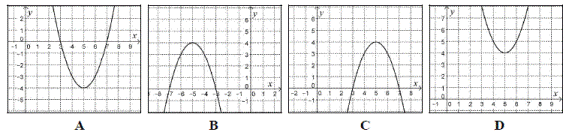
384. találat: Matematika középszintű érettségi, 2014. október, I. rész, 4. feladat
Témakör: *Algebra (egyenlet, abszolútérték) (Azonosító: mmk_201410_1r04f )

Adja meg az alábbi egyenlet megoldásait a valós számok halmazán!

385. találat: Matematika középszintű érettségi, 2014. október, I. rész, 5. feladat
Témakör: *Algebra (logaritmus, értelmezési tartomány) (Azonosító: mmk_201410_1r05f )

a) Mely valós számokra értelmezhető a$ \log_2(3-x)$kifejezés?
b) Oldja meg a valós számok halmazán az alábbi egyenletet! $ \log_2(3-x)=0$

386. találat: Matematika középszintű érettségi, 2014. október, I. rész, 6. feladat
Témakör: *Valószínűségszámítás ( számelmélet, oszthatóság) (Azonosító: mmk_201410_1r06f )

Az első 100 pozitív egész szám közül véletlenszerűen kiválasztunk egyet. Adja meg annak a valószínűségét, hogy a kiválasztott szám osztható 5-tel!

387. találat: Matematika középszintű érettségi, 2014. október, I. rész, 7. feladat
Témakör: *Algebra ( trigonometria, trigonometrikus egyenlet) (Azonosító: mmk_201410_1r07f )

Adja meg a következő egyenlet $[0; 2\pi]$ intervallumba eső megoldásának pontos értékét! $ \sin x= -1$

388. találat: Matematika középszintű érettségi, 2014. október, I. rész, 8. feladat
Témakör: *Függvények ( trigonometrikus függvény, trigonometria) (Azonosító: mmk_201410_1r08f )

Határozza meg a valós számok halmazán értelmezett $ x\mapsto 1+ \cos x$ függvény értékkészletét!

389. találat: Matematika középszintű érettségi, 2014. október, I. rész, 9. feladat
Témakör: *Koordinátageometria (Azonosító: mmk_201410_1r09f )

Egy kör érinti az y tengelyt. A kör középpontja a K(–2; 3) pont. Adja meg a kör sugarát, és írja fel az egyenletét!

390. találat: Matematika középszintű érettségi, 2014. október, I. rész, 10. feladat
Témakör: *Függvények ( másodfokú, értékkészlet, parabola) (Azonosító: mmk_201410_1r10f )

Az ábrán látható függvény értelmezési tartománya a [–2; 3] intervallum, két zérushelye –1 és 2. Az értelmezési tartományának mely részhalmazán vesz fel a függvény pozitív értéket?

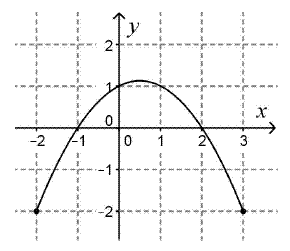
391. találat: Matematika középszintű érettségi, 2014. október, I. rész, 11. feladat
Témakör: *Algebra ( lineáris egyenletrendszer, egyenlő együtthatók) (Azonosító: mmk_201410_1r11f )

Oldja meg az alábbi egyenletrendszert a valós számpárok halmazán!

392. találat: Matematika középszintű érettségi, 2014. október, I. rész, 12. feladat
Témakör: *Algebra ( törtkitevő, hatvány, számelmélet, oszthatóság, logika,) (Azonosító: mmk_201410_1r12f )

Adja meg az alábbi állítások logikai értékét (igaz vagy hamis)!
A: Minden valós szám abszolút értéke pozitív.
B: $ 16^>=2$
C: Ha egy szám osztható 6-tal és 9-cel, akkor biztosan osztható 54-gyel is.

393. találat: Matematika középszintű érettségi, 2014. október, II. rész, 13. feladat
Témakör: *Halmazok (Venn-diagram,) (Azonosító: mmk_201410_2r13f )

Egy közvélemény-kutató intézet azt a feladatot kapta, hogy két alkalommal – fél év különbséggel – mérje fel a TV-ben látható három filmsorozat nézettségi adatait.

Az ábrán látható kérdőíven a válaszoló vagy azt jelölhette be, hogy az A, B és C sorozatok közül melyiket nézi (akár többet is meg lehetett jelölni), vagy azt, hogy egyiket sem nézi.

Az első felméréskor kapott 600 kérdőív jelöléseit összesítve megállapították, hogy az A sorozat összesen 90 jelölést kapott, a B sorozat összesen 290-et, a C sorozat pedig összesen 230-at. Érdekes módon olyan válaszadó nem volt, aki pontosan két sorozatot nézett volna, viszont 55-en mindhárom sorozatot bejelölték.

a) A válaszolók hány százaléka nézte az A sorozatot?

b) Hány válaszoló nem nézte egyik sorozatot sem?

A második felmérés után kiválogatták azokat a kérdőíveket, amelyeken valamelyik sorozat meg volt jelölve. Ezeken a három sorozat nézettségére összesen 576 jelölés érkezett. Az adatok feldolgozói minden jelölést megszámoltak, és a végeredményről az itt látható kördiagramot készítették. A második felmérés után kiválogatták azokat a kérdőíveket, amelyeken valamelyik sorozat meg volt jelölve. Ezeken a három sorozat nézettségére összesen 576 jelölés érkezett. Az adatok feldolgozói minden jelölést megszámoltak, és a végeredményről az itt látható kördiagramot készítették.

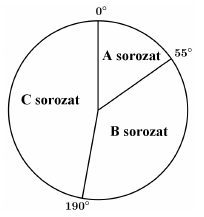
c) Számítsa ki, hogy az egyes sorozatok nézettségére hány jelölés érkezett!

394. találat: Matematika középszintű érettségi, 2014. október, II. rész, 14. feladat
Témakör: *Algebra (térgeometria, hasonlóság, ) (Azonosító: mmk_201410_2r14f )

Egy család személyautóval Budapestről Keszthelyre utazott. Útközben lakott területen belül, országúton és autópályán is haladtak. Az utazással és az autóval kapcsolatos adatokat a következő táblázat tartalmazza:

a) Mennyi ideig tartott az utazás?

b) Hány liter ezen az utazáson az autó 100 km-re eső átlagfogyasztása? Válaszát egy tizedesjegyre kerekítve adja meg!

Útközben elfogyott az autóból a benzin. A legközelebbi benzinkútnál kétféle benzineskannát lehet kapni. A nagyobbra rá van írva, hogy 20 literes, a kisebbre nincs ráírva semmi. A két kanna (matematikai értelemben) hasonló, a nagyobb kanna magassága éppen kétszerese a kisebb kanna magasságának.

c) Hány literes a kisebb kanna?

395. találat: Matematika középszintű érettségi, 2014. október, II. rész, 15. feladat
Témakör: *Térgeometria (geometria, Pitagorasz-tétel, koszinusztétel,) (Azonosító: mmk_201410_2r15f )

Egy téglatest alakú akvárium egy csúcsból kiinduló élei 30 cm, 40 cm, illetve 50 cm hosszúak.

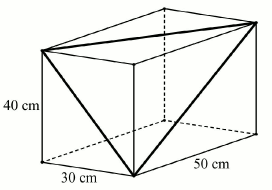
a) Hány literes ez az akvárium? (A számolás során tekintsen el az oldallapok vastagságától!)

Tekintsük azt a háromszöget, amelynek oldalait az ábrán látható téglatest három különböző hosszúságú lapátlója alkotja.

b) Mekkora ennek a háromszögnek a legkisebb szöge? Válaszát fokban, egészre kerekítve adja meg!

396. találat: Matematika középszintű érettségi, 2014. október, II. rész, 16. feladat
Témakör: *Sorozatok ( másodfokú) (Azonosító: mmk_201410_2r16f )

Egy számtani sorozat első tagja 56, differenciája –4.
a) Adja meg a sorozat első 25 tagjának összegét!
b) Számítsa ki az n értékét és a sorozat n-edik tagját, ha az első n tag összege 408.
Egy mértani sorozat első tagja 10 25 , hányadosa 0,01.
c) Hányadik tagja ennek a sorozatnak a 100 000?

397. találat: Matematika középszintű érettségi, 2014. október, II. rész, 17. feladat
Témakör: *Kombinatorika (térgeometria, kúp, kombináció, variáció) (Azonosító: mmk_201410_2r17f )

A biliárdjáték megkezdésekor az asztalon 15 darab azonos méretű, különböző színezésű biliárdgolyót helyezünk el háromszög alakban úgy, hogy az első sorban 5 golyó legyen, a másodikban 4, a következőkben pedig 3, 2, illetve 1 golyó. (A golyók elhelyezésére vonatkozó egyéb szabályoktól tekintsünk el.)

a) Hányféleképpen lehet kiválasztani a 15-ből azt az 5 golyót, amelyet majd az első sorban helyezünk el? (Az 5 golyó sorrendjét nem vesszük figyelembe.)

b) Hányféle különböző módon lehet az első két sort kirakni, ha a 9 golyó sorrendjét is figyelembe vesszük?

Egy biliárdasztal játékterülete téglalap alakú, mérete 194 cm × 97 cm. A játékterület középpontja felett 85 cm-rel egy olyan (pontszerűnek tekinthető) lámpa van, amely fénykúpjának a nyílásszöge 100°.

c) Számítással állapítsa meg, hogy a lámpa megvilágítja-e a játékterület minden pontját!

398. találat: Matematika középszintű érettségi, 2014. október, II. rész, 18. feladat
Témakör: *Kombinatorika (gráfok, statisztika, binomiális eloszlás, visszatevéses mintavétel) (Azonosító: mmk_201410_2r18f )

Egy focicsapat 11 játékosa megérkezik az edzésre, néhányan kezet fognak egymással. (Két játékos között legfeljebb egy kézfogás történik.) Az edző felírta, hogy ki hányszor fogott kezet, és a következő számokat kapta: 0; 1; 2; 2; 2; 5; 0; 0; 4; 4; 2.

a) Ábrázolja a kézfogásoknak egy lehetséges gráfját, ahol a pontok a játékosokat jelölik, és két pont között akkor van él, ha az illetők kezet fogtak az edzés előtt!

b) Hány kézfogás történt összesen?

Egy másik alkalommal az edző által feljegyzett 11 nemnegatív egész számról a következőket állapítottuk meg: a számok egyetlen módusza 2, mediánja 3, átlaga 4, terjedelme pedig 5 volt.

c) Adjon meg a fenti feltételeknek megfelelő 11 nemnegatív egész számot!

Az edzésen a játékosok a tizenegyesrúgást gyakorolják. Az egyik játékos 0,9 valószínűséggel lövi be a tizenegyest.

d) Mennyi a valószínűsége annak, hogy három rúgásból legalább egyszer betalál? A valószínűség pontos értékét adja meg!

399. találat: Matematika középszintű érettségi, 2015. május, I. rész, 1. feladat
Témakör: *Algebra (szorzattá alakítás, algebrai tört) (Azonosító: mmk_201505_1r01f )

Egyszerűsítse az $\dfrac$ törtet, ha $a\neq -1$.

400. találat: Matematika középszintű érettségi, 2015. május, I. rész, 2. feladat
Témakör: *Számelmélet (oszthatóság, oszthatósági szabály) (Azonosító: mmk_201505_1r02f )

Milyen számjegy állhat az X helyén, ha a négyjegyű $\overline$ szám 6-tal osztható?